Sphere

1. Describe the properties of the sphere and its parts:

Solution:

Sphere

r – radius
d – diameter



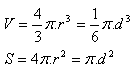Spherical layer

p1, p2 – radii of the cross-sections
v – height of the layer



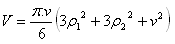Spherical segment

r – radius of the sphere
p – radius of the segment
v – height of the segment



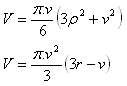Spherical sector

r – radius of the sphere
v – height of the segment



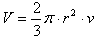Spherical cap or zone

r = radius of the sphere
v = height of the cap or zone

S = 2π.r.v

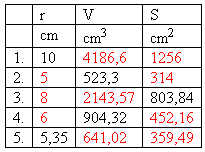
2. The table lists values characterizing spheres.

Complete the table.

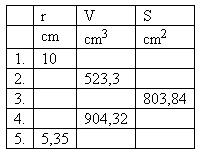
Solution:

3. Three spheres with radii r₁ = 3 cm, r₂ = 4 cm, r₃ = 5 cm are to be melted and cast into one sphere.

Solution:



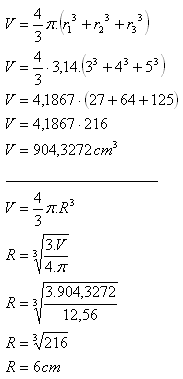
The radius of the new sphere will be R = 6 cm.

4. A cube is inscribed in a sphere with radius r = 6 cm.

Solution:



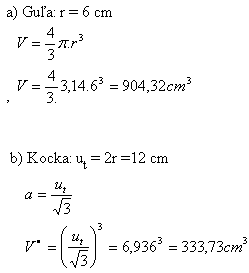
Percentage: 333.73 : 9.0432 = 36.9%
The cube’s volume is 36.9% of the sphere’s volume.

5. What is the mass of a hollow brass sphere (ρ = 8.5 g·cm^-3) if the outer diameter is D = 12 cm and the wall thickness is h = 2 mm?

Solution:

D = 12 cm
R = 6 cm
h = 2 mm = 0.2 cm
r = R – h = 6 – 0.2 = 5.8 cm
ρ = 8.5 g·cm^-3

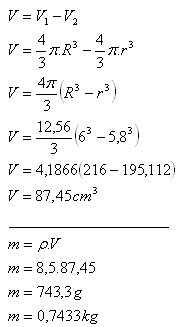
6. A sphere and a cone are inscribed in a right circular cylinder.

Solution:

Archimedes’ problem



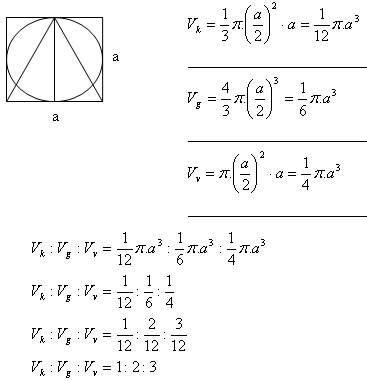
The ratio V_k : V_g : V_v = 1 : 2 : 3.

7. A planar cross-section of a sphere has length l = 125.6 cm. The distance of the section from the center of the sphere is v = 6 cm.

Solution:



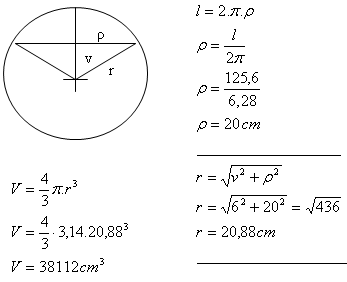
The radius of the sphere is r = 20.88 cm, its volume is V = 38112 cm³.

8. A spherical segment with height v = 5 cm has volume V = 850 cm³.

Solution:



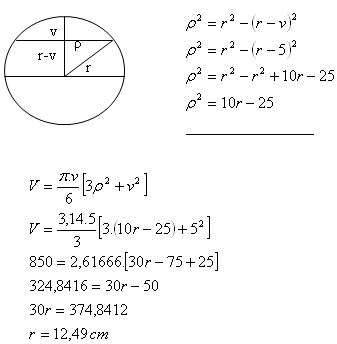
The radius of the original sphere is r = 12.49 cm.

9. The height of a spherical cap equals one third of the sphere’s radius.

Solution:



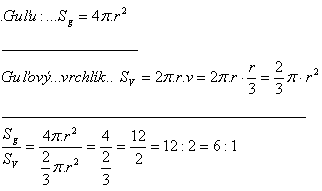
The ratio is S_g : S_v = 6 : 1.

10. Calculate the mass of a biconvex glass lens (ρ = 3.5 g·cm^-3) with diameter 10 cm and thickness 1.2 cm.

Solution:

The lens consists of two identical spherical segments.
2p = 10 cm
2v = 1.2 cm



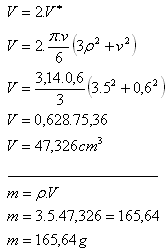
The mass of the lens is m = 165.64 g.