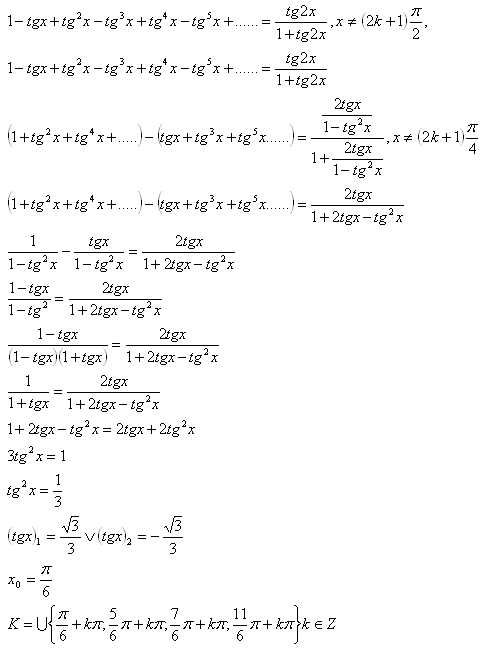Geometric Progression
1.Characterize a geometric progression:
2.Determine first 6 members of a geometric progression if stands a3 = 8 and a7 = 128.
Solution:
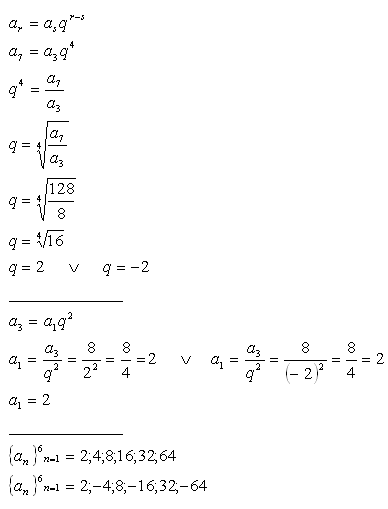
3.If a number is added to 2, 16 and 58, it results in first 3 geometric progression members. Find out the number and enumerate first 6 members of the progression.
Solution:
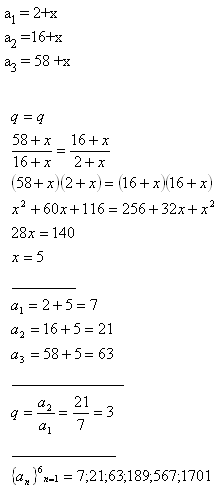
4.Insert 4 numbers between the roots of the equation x2 -66x +128 = 0 so that they would make a geometric progression.
Solution:
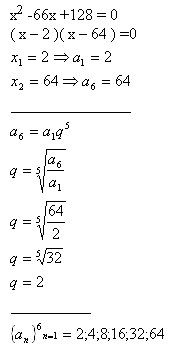
5.Enumerate first 6 progression members of a geometric progression that fits following conditions:
Solution:
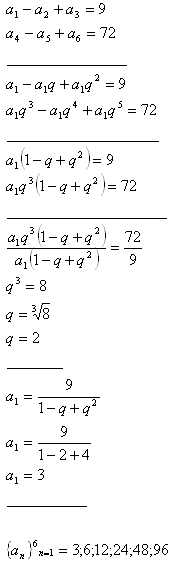
6.The surface area of a cuboid equals S = 78 cm2. The sides of the cuboid make a geometric progression. Sum of the lengths of the sides intersecting in one of the edges is 13 cm. Determine the volume of the cuboid.
Solution:
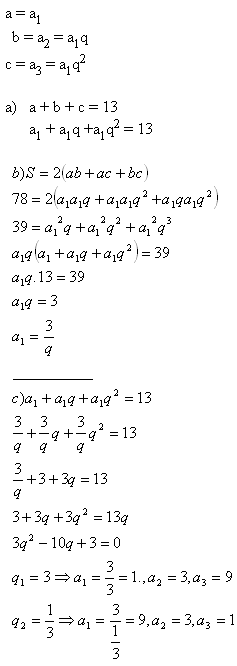
The sides lengths are a = 1cm, b = 3cm, c = 9cm.
The volume equals V = a.b.c
V = 1.3.9 cm
3
V = 27 cm
3
7.An equestrian wants to buy a horse for $10,000. He made a deal with the salesman to pay for the nails in the horseshoes. He paid 1 cent for the first nail, 2 cents for the second nail, 4 cents for the third nail and so on. Each horseshoe is fastened by 5 nails. Did he make a good deal?
Riešenie:
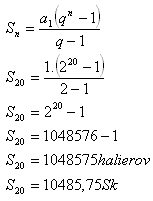
The equestrian
overbid the horse for $485,75.
8.A workman agreed to work under following conditions: His salary for the first day of work will be $1, for the second day of work $2, for the third day of work $4, and so on. How long does he have to work to earn $4095?
Solution:
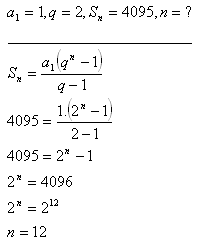
The workman needs to work for 12 days.
9.What should be the bank interest to raise the deposit of $10000 to $25 000 in 5 years?
Solution:
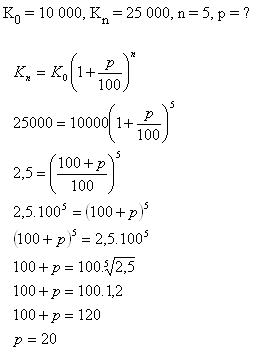
The interest should be 20%.
10.What is the sum of following infinite geometric progression?
Solution:
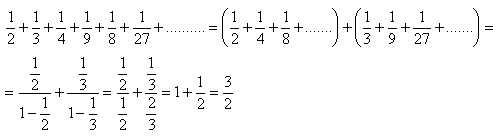
The sum of the progression members is 3/2.
11. Solve in real numbers:
Solution:
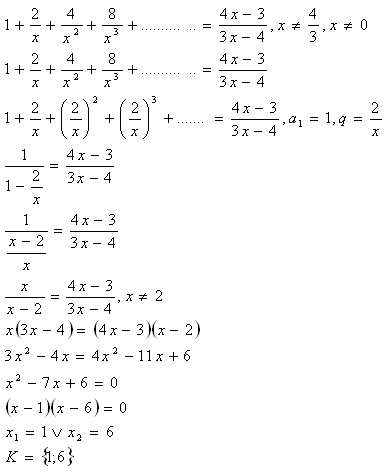
12. Solve in real numbers:
Solution: