sk|cz|en|

Physik

Dynamik

1.Mit welcher Kraft wirkt eine Person mit einer Masse von 75 kg auf den Boden einer Aufzugskabine, wenn

  • a) der Aufzug in Ruhe ist
  • b) der Aufzug sich mit einer Beschleunigung  a = 2 m·s-2 nach oben bewegt
  • c) der Aufzug sich mit einer Beschleunigung  a = 2 m·s-2 nach unten bewegt 
      (g = 10 m·s-2)

Lösung:

a)    F1 = m·g

F1 = 75 kg · 10 m·s-2 = 750 kg·m·s-2 = 750 N.

 

b) F2 = m · ( g + a )

F2 = 75 kg · 12 m·s-2 = 900 kg·m·s-2 = 900 N

 

c) F3 = m · ( g – a )

F3 = 75 kg · 8 m·s-2 = 600 kg·m·s-2 = 600 N


Die wirkenden Kräfte sind F1 = 750 N, F2 = 900 N, F3 = 600 N.

2.Auf ein Elektron wirkt in einem elektrischen Feld im Vakuum eine konstante Kraft F = 18,2·10-20 N. Welche Geschwindigkeit erreicht das Elektron (me = 9,1·10-31 kg), wenn es aus der Ruhe eine Strecke von 1 cm zurücklegt?

Lösung:

Analyse:

F = 18,2·10-20 N, me = 9,1·10-31 kg, s = 1 cm = 10–2 m.

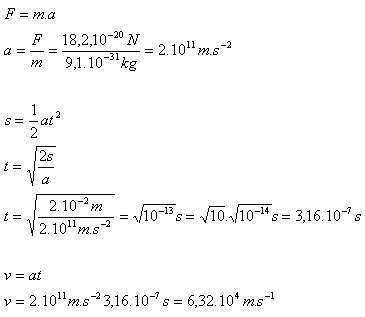
fyzika-dynamika-2 

Das Elektron erreicht eine Geschwindigkeit v = 6,32·104 m·s-1.

3.Ein Flugzeug mit einer Masse von 12 t hat eine Geschwindigkeit von 252 km·h-1. Die Triebwerke üben eine Gesamtschubkraft von 20 kN auf das Flugzeug aus. 30 % dieser Kraft werden benötigt, um Reibung und Luftwiderstand zu überwinden. Wie lang muss die Startbahn sein?

Lösung:

Analyse:

m = 12 t = 12 000 kg, v = 252 km·h-1 = 70 m·s-1,

F = 70 % von 20 000 N = 0,7 · 20 000 N = 14 000 N

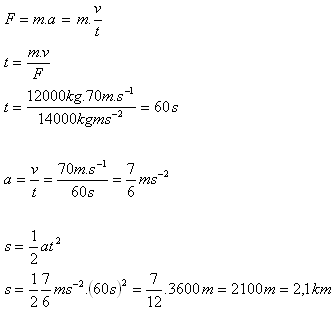
fyzika-dynamika-3

Die Startbahn muss mindestens 2,1 km lang sein.

4. a) Gib die Formeln zur Berechnung der Zentrifugal- (Zentripetal-)kraft an

b) Welche Zentripetalkraft wirkt auf eine kleine Kugel mit einer Masse von 200 g, die an einer Schnur befestigt ist, wenn sich die Kugel gleichförmig in einer Kreisbahn in der Horizontalebene bewegt? Die Schnurlänge ist 60 cm, die Geschwindigkeit 6 m·s-1.

Lösung:

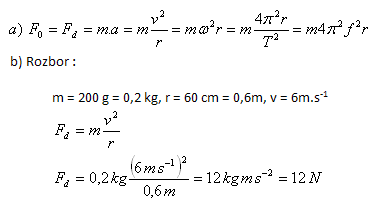
fyzika-dynamika-4

Die Zentripetalkraft auf die Kugel beträgt 12 N.

5.Während eines Kunstfluges beschreibt ein Flugzeug einen vertikalen Kreis mit einem Radius von 400 m bei einer Geschwindigkeit von 360 km·h-1. Mit welcher Anpresskraft wirkt ein Pilot mit einer Masse von 80 kg am höchsten und am niedrigsten Punkt der Bahn auf den Sitz?

Lösung:

Analyse:

v = 360 km·h-1 = 100 m·s-1, r = 400 m, m = 80 kg, g = 10 m·s-2

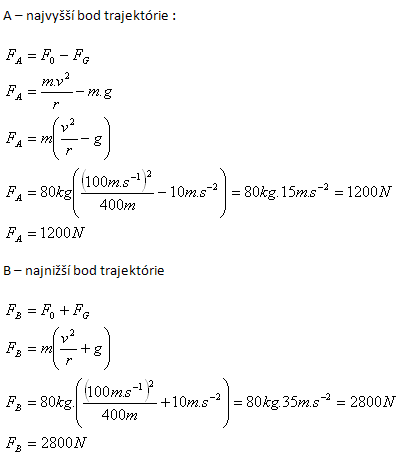
fyzika-dynamika-5
 

Der Pilot wirkt auf den Sitz mit einer Kraft FA = 1200 N bzw. FB = 2800 N.

6.Ein Auto mit einer Masse von 1 000 kg hat eine Geschwindigkeit von 54 km·h-1. Es fährt auf eine Brücke mit einem Krümmungsradius r = 50 m.

  • a)    Mit welcher Anpresskraft wirkte das Auto am oberen Punkt der Brücke auf die Straße?
  • b)    Welche Geschwindigkeit hat das Auto am oberen Punkt der Brücke?
  • c)    Was passiert, wenn die Geschwindigkeit des Autos 90 km·h-1 beträgt?

Lösung:

Analyse: m = 1000 kg, v = 54 km·h-1 = 15 m·s-1, r = 50 m, v‘ = 90 km·h-1 = 25 m·s-1

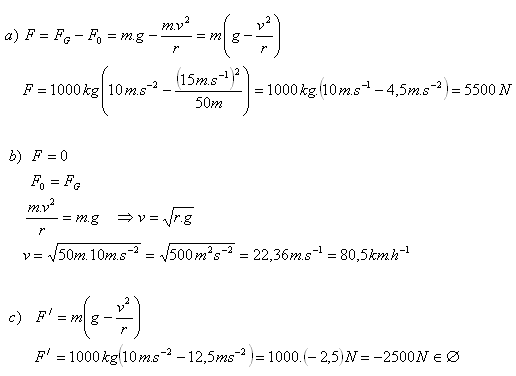
fyzika-dynamika-6 

  • a) F = 5500 N.
  • b) Die Geschwindigkeit beträgt 80,5 km·h-1.
  • c) Bei 90 km·h-1 hebt das Auto ab (es kommt zum Sprung). Das Auto geht in eine Wurfbewegung über.

7.Ein Autoreifen hat eine Masse von 6 kg. Sein Schwerpunkt liegt außerhalb des geometrischen Zentrums, daher wirkt im Schwerpunkt eine Zentrifugalkraft F0 = 3,03 N. Wie weit ist der Schwerpunkt vom Zentrum entfernt, wenn sich das Rad mit 96 U/min dreht?

Lösung:

Analyse:

m = 6 kg, F0 = 3,03 N, f = 96 U/min = 1,6 s-1

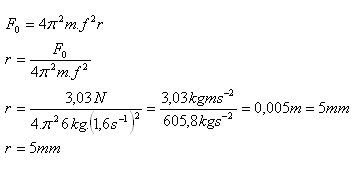
fyzika-dynamika-7

Der Abstand des Schwerpunkts vom Zentrum beträgt 5 mm.

8.Bestimme die Beschleunigung eines Körpers, der (reibungsfrei) eine geneigte Ebene der Länge l = 20 m mit der Neigung α = 5o hinabrutscht. Bestimme auch die Geschwindigkeit des Körpers am Ende der Schräge.

Lösung:

Analyse:

l = 20 m, α = 5o, g = 10 m·s-3

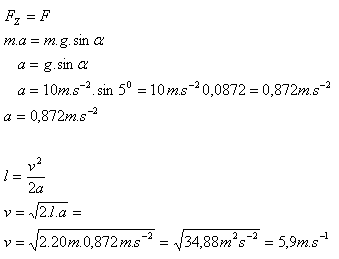
 fyzika-dynamika-8

Die Beschleunigung beträgt a = 0,872 m·s-2. Die Geschwindigkeit am Ende der Schräge beträgt etwa 6 m·s-1.

9.Wie groß ist der Gleitreibungskoeffizient zwischen Schlitten mit einer Masse von 400 kg und der Oberfläche, wenn eine Reibungskraft FT = 80 N überwunden werden muss, um die Schlitten gleichförmig in Bewegung zu halten? Bestimme außerdem, welche Holzlast die Pferde auf diesen Schlitten ziehen können, wenn ihre Zugkraft F‘T = 1400 N beträgt.

Lösung:

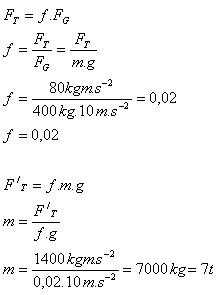
fyzika-dynamika-9 

Der Reibungskoeffizient zwischen Schlitten und Schnee ist f = 0,02. Die Pferde können 7 Tonnen Holz ziehen.

10.Ein Block mit einer Masse von 5 kg liegt auf einer geneigten Ebene mit dem Winkel α = 30o und dem Gleitreibungskoeffizienten f = 0,35. Mit welcher Kraft muss auf den Körper eingewirkt werden, damit er in Ruhe bleibt?

Lösung:

Die Gleichgewichtsbedingung auf einer geneigten Ebene lautet:

F = m g ( sin α – f cos α )

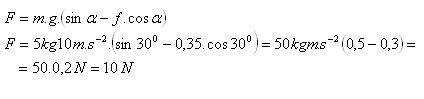
fyzika-dynamika-10 

Die erforderliche Kraft ist F = 10 N.

11.Schüttgüter werden in Depots in kegelförmigen Haufen gelagert. Berechne den Böschungswinkel, den ein frei geschüttetes Material mit der Horizontalen bildet, für

  • a)    Kohle: f = 1
  • b)    Ton: f = 0,8
  • c)    Sand: f = 0,68
(f – Gleitreibungskoeffizient)

Lösung:

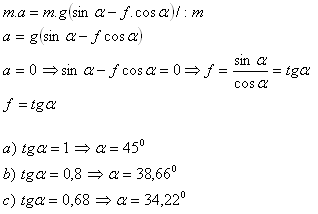
fyzika-dynamika-11 

Die Böschungswinkel sind: Kohle α = 45o, Ton α = 38,66o, Sand α = 34,22o.

12.Zwei Körper mit den Massen m1 und m2 sind über eine Rolle auf einer geneigten Ebene verbunden. Wie groß muss die Masse m2 sein, damit sie den Körper mit der Masse m1 = 8 kg in Ruhe hält, wenn der Neigungswinkel α = 40o und der Gleitreibungskoeffizient f = 0,4 ist (g = 10 m·s-2)?

Lösung:

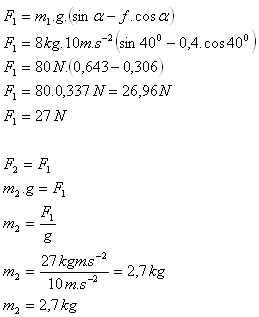
fyzika-dynamika-12 

Die Masse des zweiten Körpers ist m2 = 2,7 kg.

13.Ein Auto mit einer Masse von 2 000 kg fährt mit konstanter Geschwindigkeit einen Anstieg mit 4 % Steigung hinauf. Bestimme die Zugkraft des Motors.

Lösung:

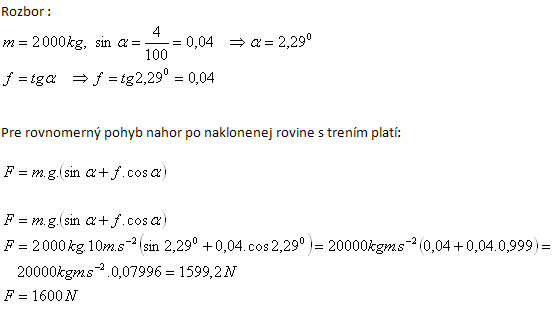
fyzika-dynamika-13 

Die Zugkraft des Motors beträgt 1600 N.

14.Ein Auto mit einer Masse von 500 kg beschleunigt mit konstanter Beschleunigung a = 2 m·s-2 einen Anstieg mit 2 % Steigung hinauf. Bestimme die Zugkraft des Motors.

Lösung:

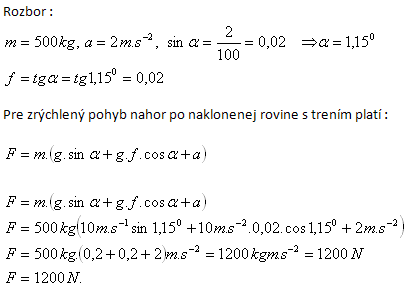
fyzika-dynamika-14 

Die Zugkraft des Motors beträgt 1200 N.

15.Ein Auto mit einer Masse von 200 kg beschleunigt bergauf (α = 5o, f = 0,09). Wie groß ist die Beschleunigung des Autos, wenn die Zugkraft des Motors 653,3 N beträgt?

Lösung:

Analyse.

m = 200 kg, F = 653,3 N, α = 5o, f = 0,09, FG = 2000 N, a = ?

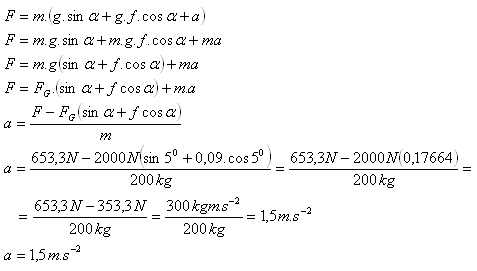
fyzika-dynamika-15 

Die Beschleunigung des Autos beträgt a = 1,5 m·s-2.

16.Eine Kugel mit einer Masse von 10 g wird mit einer Geschwindigkeit von 800 m·s-1 aus einem Gewehr mit einer Masse von 4 kg abgefeuert. Berechne die Rückstoßgeschwindigkeit des Gewehrs.

Lösung:

Analyse:

m1 = 10 g = 0,01 kg, m2 = 4 kg, v1 = 800 m·s-1, v2 = ?

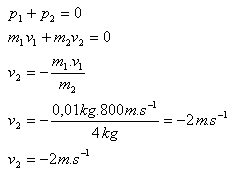
fyzika-dynamika-16

Die Rückstoßgeschwindigkeit des Gewehrs ist v2 = 2 m·s-1.

17.Eine Maschinenpistole feuert 600 Schuss pro Minute. Jede Kugel hat eine Masse von 4 g und verlässt den Lauf mit einer Geschwindigkeit von 500 m·s-1. Bestimme den Betrag der mittleren Kraft, mit der die Maschinenpistole auf die Schulter des Schützen drückt.

Lösung:

Analyse:

600 / min = 600 / 60 s, 1 Geschoss pro 60 / 600 s = 0,1 s. t = 0,1 s.

m1 = 4 g = 0,004 kg, v1 = 500 m·s-1

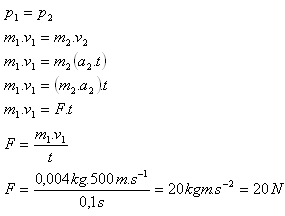
fyzika-dynamika-17 

Die Maschinenpistole drückt mit einer mittleren Kraft von F = 20 N auf die Schulter des Schützen.

18.Zwei Kugeln, die sich in gleicher Richtung bewegen, stoßen zusammen. Die erste hat eine Masse von 2 kg und bewegt sich mit 2,5 m·s-1. Die zweite hat eine Masse von 8 kg. Welche Geschwindigkeit hatte die zweite Kugel, wenn sie sich nach dem Stoß gemeinsam mit 2,1 m·s-1 bewegen?

Lösung:


Analyse:

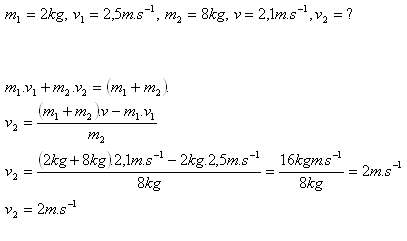
fyzika-dynamika-18 

Die zweite Kugel bewegte sich mit der Geschwindigkeit v2 = 2 m·s-1.

19.Ein Projektil der Masse 100 kg, das sich entlang einer Eisenbahnlinie mit 500 m·s-1 bewegt, trifft einen Wagen mit Sand der Masse 10 t und bleibt darin stecken. Welche Geschwindigkeit hat der Wagen nach dem Aufprall, wenn er sich vor der Kollision mit 36 km·h-1 bewegte

  • a)    dem Projektil entgegen
  • b)    in Richtung des Projektils

Lösung:

Analyse:

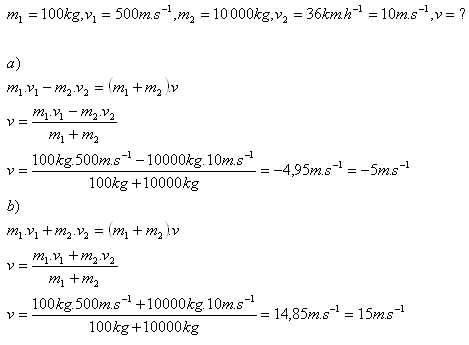
fyzika-dynamika-19

20. Ein Junge mit einer Masse von 60 kg steht auf Schlittschuhen auf glattem Eis. Er setzt sich in Bewegung, indem er einen Eisblock der Masse 6 kg mit der Geschwindigkeit 3 m·s-1 wegwirft. Wie weit legt der Junge durch den Wurf zurück, wenn er sich 9 Sekunden lang bewegt?

Lösung:

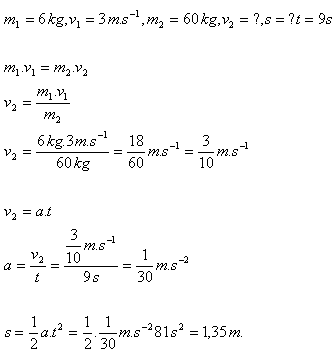
fyzika-dynamika-20 

Der Schlittschuhläufer legt eine Strecke von 1,35 m zurück.