Hydrodynamik

1. Lassen Sie uns einige grundlegende Eigenschaften der Strömung betrachten.

Lösung:

Stationäre Strömung ist eine Bewegung eines Fluids (Gases), bei der sich jedes Teilchen in dieselbe Richtung und mit derselben Geschwindigkeit bewegt.

Es gilt:

a.) Volumenstrom: $Q = S \cdot v$

b.) Massenstrom: $Q_m = S \cdot v \cdot \rho$

c.) Kontinuitätsgleichung: $S_1 \cdot v_1 = S_2 \cdot v_2$

d.) Bernoulli-Gleichung:

$p_1 + \tfrac{1}{2} \rho v_1^2 = p_2 + \tfrac{1}{2} \rho v_2^2$ $p_1 = \rho g h_1 \quad \text{– hydrostatic pressure}$ $p_2 = \rho g h_2 \quad \text{– hydrostatic pressure}$ $p_1' = \tfrac{1}{2} \rho v_1^2 \quad \text{– hydrodynamic pressure}$ $p_2' = \tfrac{1}{2} \rho v_2^2 \quad \text{– hydrodynamic pressure}$

e.) Austrittsgeschwindigkeit einer Flüssigkeit (Torricelli-Formel)

v = \sqrt{2 g h}

d = v \sqrt{\tfrac{2H}{g}}

$h$ – Abstand der Öffnung im Gefäß von der Flüssigkeitsoberfläche
$H$ – Abstand der Öffnung im Gefäß vom Boden

f.) Umströmung eines realen Körpers (Newtonsches Gesetz)

Gilt auch für Gase (Luft):

F = \tfrac{1}{2} C \cdot S \cdot \rho v^

2.Eine Rohrleitung mit veränderlichem Querschnitt fördert 5 Liter Wasser pro Sekunde. Wie groß ist die Strömungsgeschwindigkeit in Querschnitten mit den Flächen

a.) S₁ = 20 cm²
b.) S₂ = 100 cm²

Lösung:

Analyse:

Q = 5 l.s^-1 = 5 dm³.s^-1 = 0.005 m³.s^-1, S₁ = 20 cm² = 0.002 m², S₂ = 0.01 m²

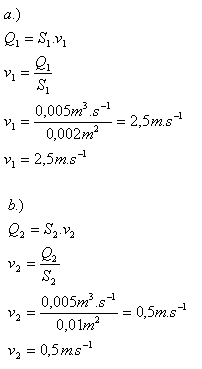
Die Strömungsgeschwindigkeiten sind v₁ = 2.5 m.s^-1 und v₂ = 0.5 m.s^-1.

3.Ein kleines Wasserkraftwerk nutzt die Energie von Wasser, das aus einer Höhe von 4 m in eine Turbine strömt. Bei welchem Volumenstrom hat die Turbine eine Leistung von 600 kW, wenn ihr Wirkungsgrad 75 % beträgt?

Lösung:

Analyse:

h = 4 m, P = 600·10³ W, η = 0.75, ρ = 1000 kg.m^-3, g = 10 m.s^-2

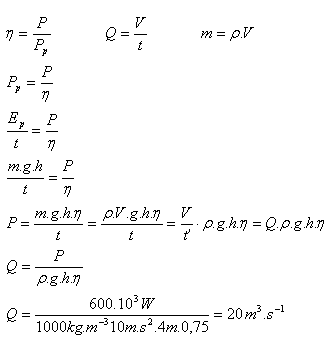
Die Turbine erreicht die geforderte Leistung bei einem Volumenstrom von Q = 20 m³.s^-1

4.Eine Pumpe fördert 300 l Wasser in 1 Minute. Das Saugrohr hat einen Durchmesser von 80 mm, durch das Druckrohr fließt das Wasser mit einer Geschwindigkeit von 8 m.s^-1. Bestimmen Sie die Geschwindigkeit des Wassers im Saugrohr und den Durchmesser des Druckrohrs.

Lösung:

Analyse:

d₁= 80 mm = 0.08 m, r₁ = 0.04 m, v₂ = 8 m.s^-1

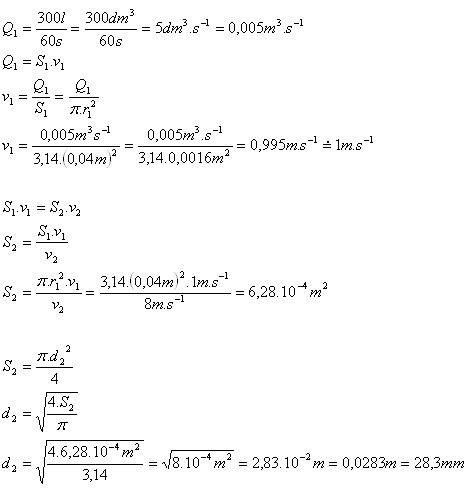
Die Geschwindigkeit des Wassers im Saugrohr beträgt etwa v₁ = 1 m.s^-1.
Der Durchmesser des Druckrohrs ist d₂ = 28.3 mm.

5.Im weiteren Teil eines Rohres fließt Wasser mit v₁ = 10 cm.s^-1. Wie groß ist die Geschwindigkeit im engeren Teil, der den halben Radius hat?

Lösung:

Analyse:

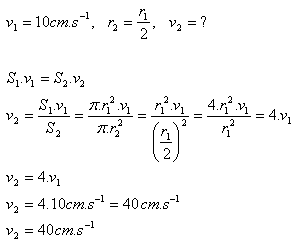
Im engeren Teil fließt das Wasser mit v₂ = 40 cm.s^-1

6.Dieselkraftstoff (ρ = 830 kg.m^-3) wird durch ein Rohr mit Durchmesser 40 cm bei einer Geschwindigkeit von 1.5 m.s^-1 transportiert. Bestimmen Sie

a.) den hydrodynamischen Druck im Rohr
b.) die in 1 Stunde transportierte Masse Diesel

Lösung:

Analyse:

d = 40 cm = 0.4 m, r = 0.2 m, v = 1.5 m.s^-1, t = 1 h = 3600 s, ρ = 830 kg.m^-3

Der hydrodynamische Druck im Rohr beträgt p = 934 Pa.
Die Masse des Diesels beträgt m = 563 Tonnen.

7.In einem horizontalen Rohr mit Durchmesser d₁ = 5 cm fließt Wasser mit v₁ = 2 m.s^-1 und p₁ = 2·10⁵ Pa. Wie groß ist der Druck im engeren Teil des Rohrs mit d₂ = 2 cm?

Lösung:

Analyse:

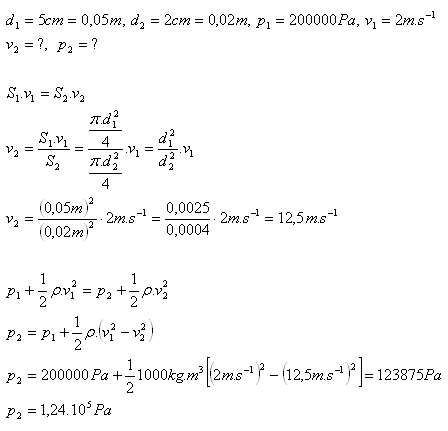
Der Druck der Flüssigkeit im engeren Teil ist p₂ = 1.24·10⁵ Pa.

8.In einer Wasserleitung fließt Wasser mit 2.24 m.s^-1 und hat einen Druck von 0.1 MPa. Wie groß ist die Geschwindigkeit im verengten Teil, wo der Druck 0.09 MPa beträgt?

Lösung:

Analyse:

v₁ = 2.24 m.s^-1, p₁ = 0.1 MPa = 0.1·10⁶ Pa, p₂ = 0.09 MPa = 0.09·10⁶ Pa

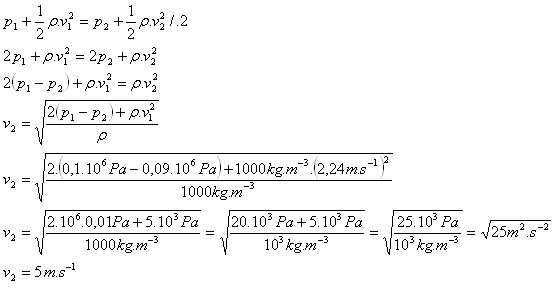
Die Geschwindigkeit des Wassers im verengten Teil ist v₂ = 5 m.s^-1

9.In der Wand eines mit Wasser gefüllten Behälters befindet sich ein Loch 45 cm unterhalb der freien Oberfläche. Der Behälter steht am Rand eines Tisches, sodass das Loch 80 cm über dem Boden liegt. In welcher Entfernung vom Tischrand trifft der Wasserstrahl auf den Boden, wenn das Loch geöffnet wird?

Lösung:

Analyse:

h = 45 cm = 0.45 m, H = 80 cm = 0.8 m

Die Auftreffentfernung des Wasserstrahls ist d = 1.2 m.

10.Ein zylindrischer Behälter wird mit 18.84 Litern Wasser pro Minute befüllt. Gleichzeitig fließt Wasser durch ein Loch am Boden mit Durchmesser 1 cm aus. Auf welcher Höhe stabilisiert sich der Wasserstand bei idealem Ausströmen der Flüssigkeit?

Lösung:

Analyse:

d = 1 cm, r = 0.5 cm = 0.005 m

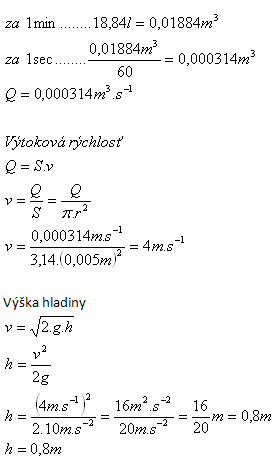
Der Wasserstand stabilisiert sich bei h = 0.8 m.

11.Welche hydrodynamische Widerstandskraft wirkt auf eine Kugel mit Radius r = 2.5 cm, wenn Wasser sie mit v = 1.8 m.s^-1 umströmt. C = 0.48

Lösung:

Analyse:

r = 2.5 cm = 0.025 m, v = 1.8 m.s^-1, C = 0.48, ρ = 1000 kg.m^-3

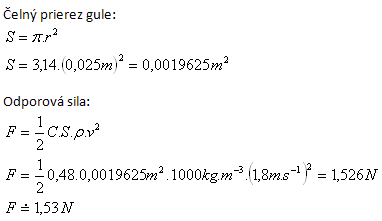
Die Widerstandskraft beträgt etwa F = 1.53 N.

12.Mit welcher Geschwindigkeit fällt ein Regentropfen, wenn seine Masse 0.005 g, der Radius 2.26 mm beträgt. ρ (Luft) = 1.3 kg.m^-3, C = 0.4

Lösung:

Analyse:

m = 0.005 g = 5·10^-6 kg, r = 2.26 mm = 2.26·10^-3 m, ρ (Luft) = 1.3 kg.m^-3, C = 0.4

Stirnfläche: S = π·r² = 3.14·(2.26·10^-3 m)² = 16·10^-6 m²

Widerstandskraft: F = m·g = 5·10^-6 kg·10 m.s^-2 = 5·10^-5 N

Fallgeschwindigkeit des Tropfens:

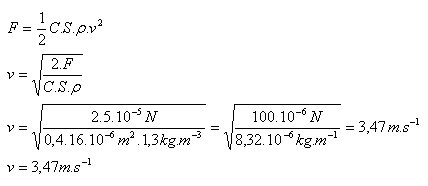
Der Regentropfen fällt mit v = 3.4 m.s^-1

13.Auf ein U-Boot wirkt eine hydrodynamische Widerstandskraft von 3600 N. Das U-Boot hat eine Stirnfläche von 15 m² und bewegt sich mit 14.4 km.h^-1. Bestimmen Sie den Widerstandsbeiwert C!

Lösung:

Analyse:

F = 3600 N, S = 15 m², v = 14.4 km.h^-1 = 4 m.s^-1, C = ?

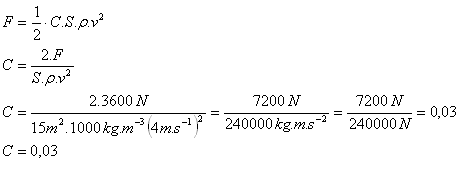
Der Widerstandsbeiwert des U-Boots ist C = 0.03

14.Berechnen Sie die Endgeschwindigkeit eines Fallschirmspringers mit Gesamtmasse 80 kg, wenn ein halbkugelförmiger Fallschirm den Radius 5 m, den Widerstandsbeiwert 1.33 und die Luftdichte 1.3 kg.m^-3 hat.

Lösung:

Analyse:

m = 80 kg, r = 5 m, C = 1.33, ρ = 1.3 kg.m^-3, v = ?

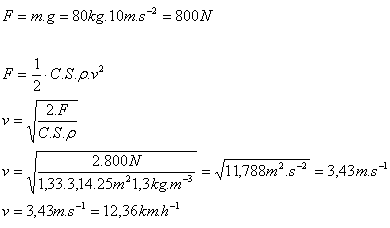
Der Fall des Fallschirmspringers stabilisiert sich bei v = 12.36 km.h^-1

15.

Wie groß ist der Radius eines Glaskügelchens (ρ_S = 2500 kg.m^-3), wenn es in Wasser (ρ = 1000 kg.m^-3) mit konstanter Geschwindigkeit v = 2 m.s^-1 fällt. C = 0.48

Lösung:

Analyse:

ρ_S = 2500 kg.m^-3, ρ = 1000 kg.m^-3, v = 2 m.s^-1, C = 0.48

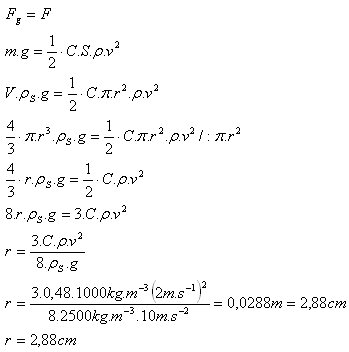
Das Glaskügelchen hat den Radius r = 2.88 cm.

Physik

Hydrodynamik

Adblock detected