Bewegungen in einem radialen Gravitationsfeld
1. Charakterisieren Sie das radiale Gravitationsfeld der Erde.
Lösung:
Wenn die Trajektorie eines materiellen Punktes bei der Bewegung im Gravitationsfeld der Erde mit den Abmessungen der Erde vergleichbar ist, ist das Gravitationsfeld radial. Ein radiales Gravitationsfeld ist räumlich unbegrenzt. An verschiedenen Orten eines solchen Feldes hat die Gravitationsbeschleunigung unterschiedliche Richtung, da sie stets zum Erdzentrum zeigt, und unterschiedlichen Betrag, der von der Entfernung des jeweiligen Ortes vom Erdzentrum abhängt. Beispiele für Bewegungen im radialen Gravitationsfeld der Erde sind die Bewegungen künstlicher Erdsatelliten, interkontinentaler Geschosse und Raketen usw.
Auf einen Körper der Masse m wirken bei der Bewegung im Gravitationsfeld der Erde
a) Zentripetalkraft:
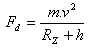
b) Gravitationskraft:
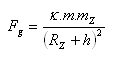
Der Körper besitzt
a) kinetische Energie:
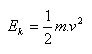
b) potenzielle Energie:
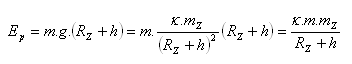
Für das radiale Gravitationsfeld der Sonne gelten die drei Keplerschen Gesetze:
1.) Die Planeten bewegen sich um die Sonne auf Ellipsen, die nur wenig von Kreisen abweichen; in einem gemeinsamen Brennpunkt befindet sich die Sonne.
2.) Die von dem Fahrstrahl eines Planeten in gleichen Zeiten überstrichenen Flächen sind gleich.
3.)
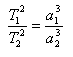
T
1, T
2 sind die Umlaufzeiten zweier Planeten, a
1, a
2 sind die großen Halbachsen ihrer Bahnen.
2.Berechnen Sie die erste und die zweite kosmische Geschwindigkeit.
Lösung:
- a.) Erste kosmische Geschwindigkeit v1
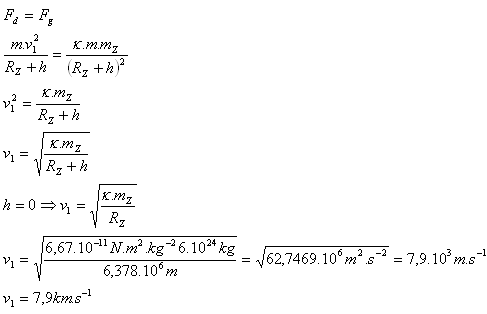
- b.) Zweite kosmische Geschwindigkeit v2
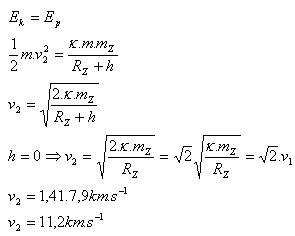
- Die erste kosmische (kreisförmige) Geschwindigkeit ist v1 =7,9 km.s-1.
- Die zweite kosmische (parabolische, Flucht-)Geschwindigkeit ist v2 = 11,2 km.s-1. Der Körper entfernt sich dauerhaft von der Erde, bleibt jedoch im Gravitationsfeld der Sonne.
- Die dritte kosmische Geschwindigkeit ist v3 = 16,7 km.s-1. Der Körper verlässt das Gravitationsfeld der Sonne.
3. Zu einem bestimmten Zeitpunkt wurden von der Erde zwei Satelliten in unterschiedlichen Höhen (h1 = RZ, h2 = 2RZ) beobachtet, die sich auf kreisförmigen Bahnen in gleicher Richtung bewegten. Bestimmen Sie ihre Geschwindigkeiten. v1 = 7,9 km.s-1
Lösung:
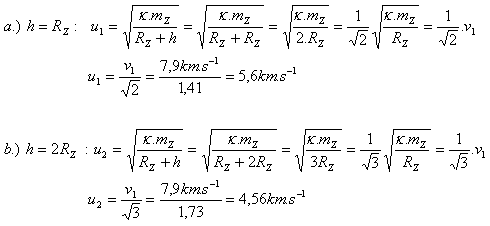
Die Geschwindigkeiten der Satelliten sind u1 = 5,6 km.s-1 und u2 = 4,56 km.s-1.
4.Bestimmen Sie die parabolische (zweite kosmische) Geschwindigkeit an der Oberfläche des Mondes. mM=7,41.1022 kg, RM=1,736.106 m
Lösung:
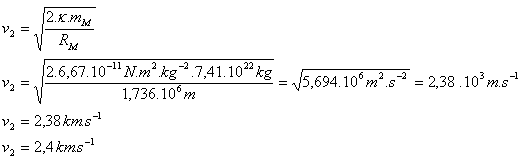
Die zweite kosmische Geschwindigkeit an der Oberfläche des Mondes ist v2 = 2,4 km.s-1
5. Die Masse der Sonne ist mS =1,989 1030 kg. Die Umlaufgeschwindigkeit der Erde um die Sonne beträgt v = 29,82 km.s-1. In welchem Abstand umläuft die Erde die Sonne?
Lösung:
Analyse:
mS =1,989 1030 kg, v = 29,82 km.s-1= 29,82.103 m.s-1
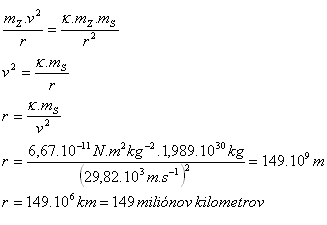
r (genau) = 149 597 900 km
Es kann der gerundete Wert AU = 150.106 km verwendet werden. Das ist die „Astronomische Einheit“.
6. Der Mond umläuft die Erde in einer Entfernung von 384 000 km und hat eine Masse von 7,41.1022 kg. Finden Sie auf der Verbindungslinie der Schwerpunkte beider Körper den Punkt C, in dem ein Mensch schwerelos wäre. In diesem Punkt ist die Gravitationskraft der Erde gleich der Gravitationskraft des Mondes.
Lösung:
Analyse:
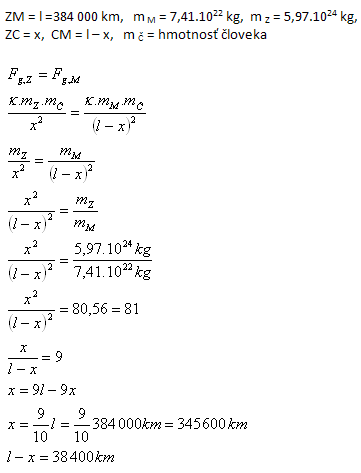
Der gesuchte Punkt C (Librationspunkt, Lagrange-Punkt) befindet sich in einer Entfernung von 345 600 km von der Erde und 38 400 km vom Mond.
7.Der größte Planet des Sonnensystems, Jupiter, umläuft die Sonne in einer Entfernung von 7,8.108 km. Die Masse der Sonne beträgt 1,989.1030 kg. Welche Masse hat der Jupiter, wenn ihn die Sonne mit der Gravitationskraft Fg= 4,2.1023 N anzieht? Wie groß ist die Beschleunigung, die die Sonne dem Jupiter erteilt? Wie groß ist die Umlaufzeit (Periode T) des Jupiter um die Sonne?
Lösung:

Die Masse des Jupiter beträgt 1,9.1027 kg, seine Beschleunigung 2,2.10-4 m.s-2. Die Umlaufzeit des Jupiter um die Sonne beträgt 11,8 Jahre (Erdjahre).
8. In welcher Höhe h über der Erde muss ein geostationärer Satellit platziert werden, der sich über demselben Ort über der Erdoberfläche befindet?
Lösung:
Analyse:
mZ = 6.1024 kg, RZ = 6,378.106m, TZ = 23 Std. 56 Min. 4 s = 8,6164.104s
mD = Masse des Satelliten
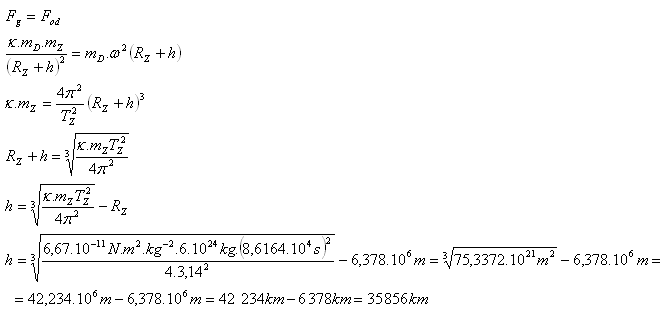
Der geostationäre Satellit muss in einer Höhe von 35 856 km über der Erde platziert werden.
9. Mithilfe der Keplerschen Gesetze ist zu bestimmen:
- a.) Wie groß ist die mittlere Entfernung des Planeten Venus von der Sonne, wenn seine Umlaufzeit
TV=0,615 Jahre beträgt.
- b.) Wie groß ist die Umlaufzeit des Planeten Merkur um die Sonne, wenn seine mittlere Entfernung von der Sonne
aM = 0,387AU beträgt
Lösung:

- Die Entfernung der Venus von der Sonne beträgt etwa 108,5.106 km.
- Die Umlaufzeit des Merkur um die Sonne beträgt etwa 88 Tage.
10. Ein Raumschiff startet von der geostationären Raumstation in der Höhe h = 35 856 km über der Erde (siehe Aufgabe Nr. 8) in Richtung Mond. Nach welcher Zeit gelangt das Raumschiff in den Bereich des Mondes?
Lösung:
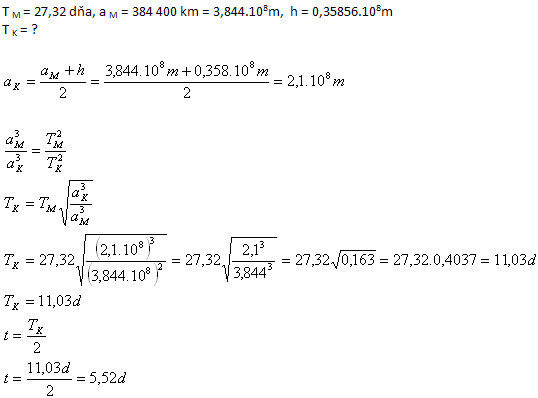
Die Zeit 11,03 Tage ist die Periode der gesamten Bahn des Raumschiffs. Der Flug von der Erde zum Mond dauert die Hälfte dieser Periode, also etwa 5,52 Tage.