Energie
1.Beschreiben Sie kurz die physikalische Größe Energie.
Lösung:
Energie ist die Fähigkeit von Körpern, Arbeit zu verrichten.
Energie:
- 1.) kinetische (Bewegungs-) Energie Ek
- 2.) potenzielle (Lage-) Energie Ep
1.) Kinetische Energie. Jeder Körper, der sich bewegt, besitzt kinetische Energie.
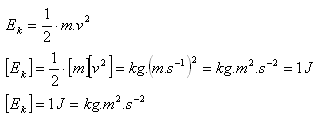
2.) Potenzielle Gravitationsenergie. Jeder Körper, der sich in einer bestimmten Höhe über der Erde befindet, besitzt potenzielle Energie.
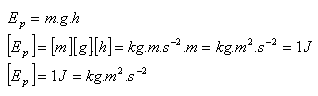
Gesetz der Erhaltung der mechanischen Energie:
In einem isolierten System Körper – Erde bleibt die gesamte mechanische Energie konstant. Zu jedem Zeitpunkt ist die Summe aus kinetischer und potenzieller Energie konstant.
E = Ek + Ep = konst.
2.Ein Ford Fusion mit einer Masse von 1156 kg hat seine Geschwindigkeit von 18 km/h auf 72 km/h erhöht. Um wie viel hat sich seine kinetische Energie vergrößert?
Lösung:
Analyse:
m = 1156 kg, v1 = 18 km/h = 5 m/s, v2 = 72 km/h = 20 m/s
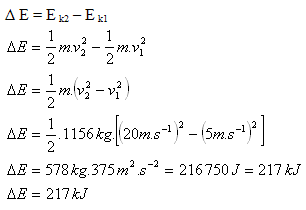
Die kinetische Energie des Autos hat um ΔE = 217 kJ zugenommen.
3.In welchem Verhältnis stehen die kinetischen Energien von zwei Kugeln, wenn die zweite doppelt so schwer und viermal so schnell ist wie die erste?
Lösung:
Analyse:
m2 = 2·m1, v2 = 4·v1
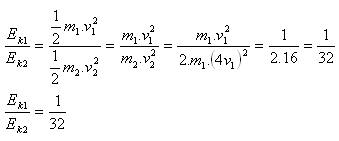
Die kinetischen Energien stehen im Verhältnis 1 : 32.
4.Ein Schiff fährt mit 36 km/h über einen See. An Bord geht ein Seemann mit einer Masse von 80 kg mit einer Geschwindigkeit von 2 m/s. Berechnen Sie seine kinetische Energie relativ zum See, wenn er
- a.) in Fahrtrichtung geht
- b.) gegen die Fahrtrichtung geht
Lösung:
Analyse:
m = 80 kg, v1 = 36 km/h = 10 m/s, v2 = 2 m/s
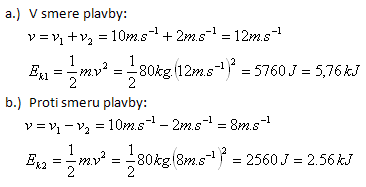
Die kinetische Energie des Seemanns beträgt:
5.Ein Zug mit einer Masse von 200 Tonnen fährt mit 54 km/h. Beim Bremsen wirken die Bremsen eine Kraft, deren Größe auf je 1000 kg Zugmasse 300 N beträgt. Bestimmen Sie:
- a.) die kinetische Energie des Zuges vor dem Bremsen
- b.) die Arbeit, die die Bremsen verrichten müssen, damit der Zug stoppt
Lösung:
Analyse:
m = 200 t = 2·105 kg, v = 54 km/h = 15 m/s
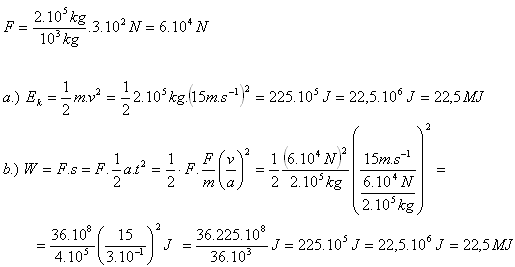
Die Arbeit, die die Bremsen verrichten müssen, um den Zug zu stoppen, entspricht der kinetischen Energie des Zuges vor dem Bremsen.
Ek = W = 22,5 MJ
6.Ein Gewicht von 2 kg befindet sich 50 cm über der Tischoberfläche. Der Tisch ist 1,5 m über dem Boden. Bestimmen Sie die potenzielle Energie des Gewichts:
- a.) relativ zur Tischoberfläche
- b.) relativ zum Boden
Lösung:
- a.) Relativ zur Tischoberfläche
m = 2 kg, h1 = 0,5 m, g = 10 m/s²
Ep1 = m·g·h1 = 2 kg · 0,5 m · 10 m/s² = 10 J
m = 2 kg, h2 = 0,5 m + 1,5 m = 2 m, g = 10 m/s²
Ep2 = m·g·h2 = 2 kg · 2 m · 10 m/s² = 40 J
Die potenzielle Energie des Gewichts beträgt relativ zum Tisch 10 J, relativ zum Boden 40 J.
7.Ein Vorschlaghammer mit einer Masse von 400 kg fällt aus 3 m Höhe. Beim Aufprall dringt der Pfahl 60 cm in den Boden. Wie groß ist die durchschnittliche Kraft, die den Boden überwinden muss?
Lösung:
Analyse:
m = 400 kg, h = 3 m, s = 60 cm = 0,6 m, g = 10 m/s², F = ?
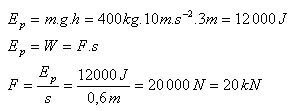
Die durchschnittliche Kraft beträgt F = 20 kN.
8.Ein Stein mit einer Masse von 300 g fällt frei von einem Turm, 45 m hoch. Bestimmen Sie die gesamte mechanische Energie des Steins relativ zur Erde nach der ersten Sekunde.
Lösung:
Analyse:
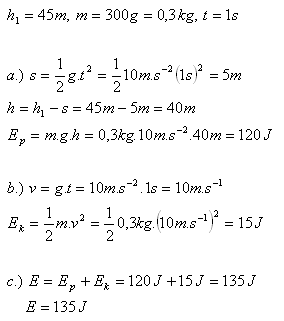
Die gesamte mechanische Energie des Steins beträgt E = 135 J.
9.α-Teilchen werden beim radioaktiven Zerfall von Elementen emittiert. Sie haben eine Masse von 6,6·10-27 kg und eine Geschwindigkeit von 2·104 km/s. Wie viele α-Teilchen verrichten bei der Bremsung in schwerem Wasser Arbeit von 1 J?
Lösung:
Analyse:
m = 6,6·10-27 kg, v = 2·104 km/s = 2·107 m/s, W = 1 J
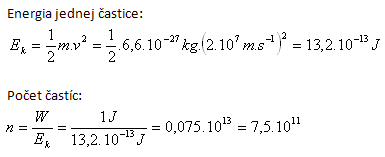
Die erforderliche Arbeit wird von 7,5·1011 Teilchen verrichtet.
10.Eine Berghütte wurde von einem Stein mit einer Masse von 120 kg beschädigt, der ursprünglich 20 m über der Hütte hing. Mit welcher Geschwindigkeit traf der Stein die Hütte? Wie groß wäre die Geschwindigkeit, wenn der Stein nur 60 kg hätte?
Lösung:
Analyse:
m = 120 kg, h = 20 m
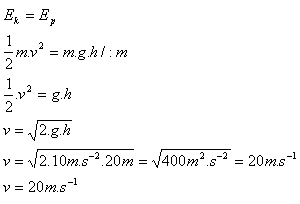
Der Stein traf die Hütte mit v = 20 m/s.
Die Fallgeschwindigkeit hängt nicht von der Masse des fallenden Körpers ab.
11.Eine Kugel mit einer Masse von 200 g schwingt an einer dünnen Schnur. Beim Durchgang durch die tiefste Position beträgt ihre Geschwindigkeit 3 m/s. Welche maximale Höhe erreicht die Kugel beim Ausschlag?
Lösung:
Analyse:
m = 200 g = 0,2 kg, v = 3 m/s, g = 10 m/s²
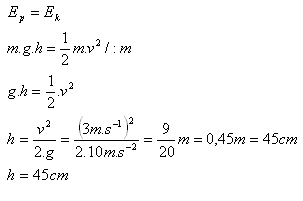
Die Kugel erreicht eine maximale Höhe von h = 45 cm.
12.Ein Körper mit einer Masse von 2 kg wird senkrecht nach oben geworfen. In 15 m Höhe hat er eine kinetische Energie von 450 J. Welche maximale Höhe erreicht der Körper?
Lösung:
Analyse:
m = 2 kg, Ek15 = 450 J, h15 = 15 m
a.) Gesamtenergie des Körpers in 15 m Höhe: E15 = Ek15 + Ep15 = 450 J + 2·10·15 = 750 J
b.) Gesamtenergie des Körpers in der maximalen Höhe: Emax = 750 J, Ek = 0
Emax = Ek + Ep = 0 + m·g·h
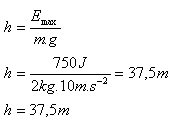
Der Körper erreicht eine maximale Höhe von h = 37,5 m.
13.Eine 6 g schwere Kugel, die sich mit 350 m/s bewegt, durchschlägt ein 20 cm dickes Holzbrett und verlässt es mit 150 m/s. Bestimmen Sie den mittleren Wert der Kraft, mit der die Kugel auf das Brett wirkte.
Lösung:
Analyse:
m = 6 g = 0,006 kg, s = 20 cm = 0,2 m, v1 = 350 m/s, v2 = 150 m/s
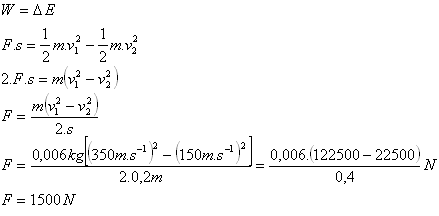
Die Kugel wirkte mit F = 1500 N auf das Brett.
14.Ein Wagen mit einer Masse von 250 kg fährt auf horizontalen Schienen mit 2,4 m/s und stößt auf einen gleich schweren Wagen, der mit 1,8 m/s fährt. Nach dem Aufprall verbinden sich die Wagen und bewegen sich gemeinsam weiter. Berechnen Sie, welcher Teil der mechanischen Energie beim Aufprall in andere Energieformen umgewandelt wird, wenn die Wagen sich vor dem Aufprall
- a.) hintereinander bewegen
- b.) aufeinander zufahren
Lösung:
Analyse:
m1 = 250 kg, v1 = 2,4 m/s, m2 = 250 kg, v2 = 1,8 m/s
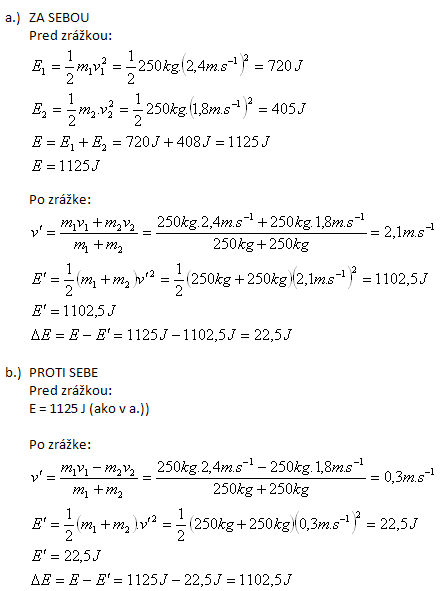
In andere Energieformen umgewandelt:
- a.) ΔE = 22,5 J
- b.) ΔE = 1102,5 J
15.Ein Eisenbahnwagen mit einer Masse von 10 Mg stößt bei 4 m/s auf einen festen Puffer. Um welche Länge wird die Feder des Puffers zusammengedrückt, wenn ihre Steifigkeit 4 MN/m beträgt? (Verwendung der potentiellen Energie der Feder Ep = 1/2·k·y², wobei k = Federsteifigkeit, y = Verlängerung oder Kompression der Feder)
Lösung:
Analyse:
m = 10 Mg = 104 kg, k = 4 MN/m, v = 4 m/s
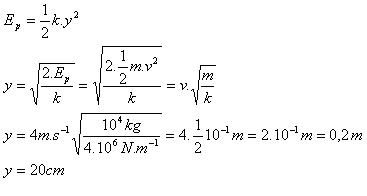
Die Feder wird um 20 cm zusammengedrückt.