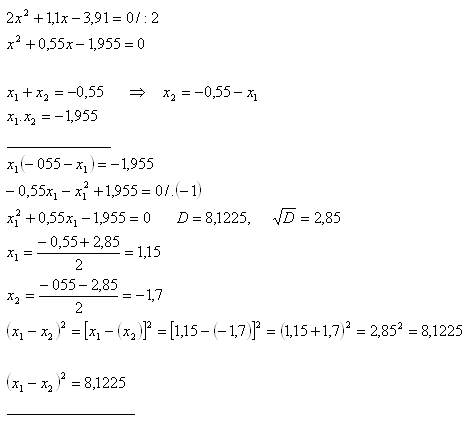Eigenschaften der Wurzeln einer quadratischen Gleichung
1. Stellen Sie die quadratische Gleichung x2 +px +q = 0 auf, wenn p = -(x1+x2) und q = x1·x2 :
Lösung:
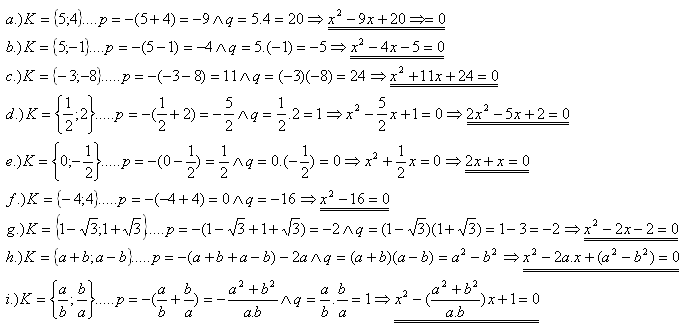
2. Bestimmen Sie die Zahl „k“, sodass eine Wurzel der Gleichung x2-5x+k=0 gleich x1=3 ist.
Lösung:
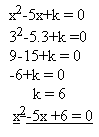
3. Bestimmen Sie die Zahl „k“, sodass eine Wurzel der Gleichung kx2-15x+7=0 gleich x1=7 ist.
Lösung:
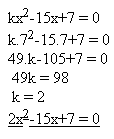
4. Bestimmen Sie die Zahl „k“, sodass eine Wurzel der Gleichung x2+kx+20=0 gleich x1=10 ist.
Lösung:
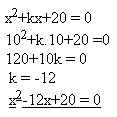
5. Bestimmen Sie die Zahl „a“, sodass für die Wurzeln der Gleichung x2-3ax-4a2=0 gilt: x1-x2=10.
Lösung:
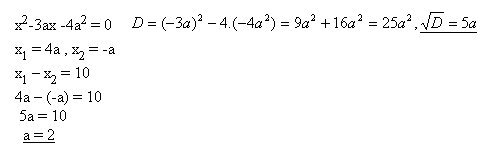
6. Für welche reellen Zahlen „m“ hat die Gleichung x2+3x-2m2+m+3=0 eine Wurzel, die gleich Null ist? Berechnen Sie auch die zweite Wurzel der Gleichung.
Lösung:
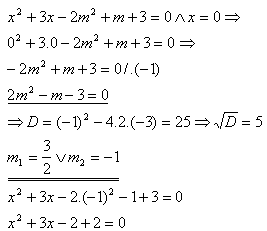
7. Gegeben ist die Gleichung x2-13x+36=0. Schreiben Sie die Gleichung mit den Wurzeln y1,y2, für die gilt:
Lösung:
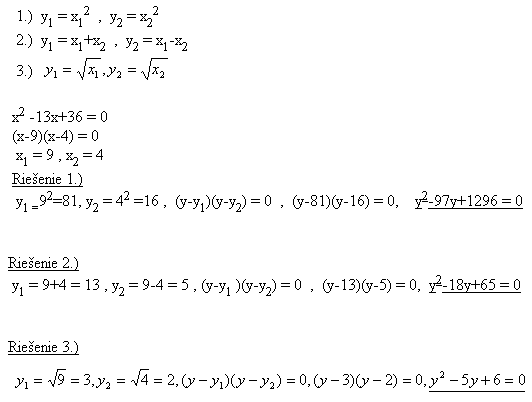
8. Gegeben ist die Gleichung x2 – 6x +8 = 0. Stellen Sie eine Gleichung auf, deren Wurzeln die Bedingung erfüllen:
Lösung:
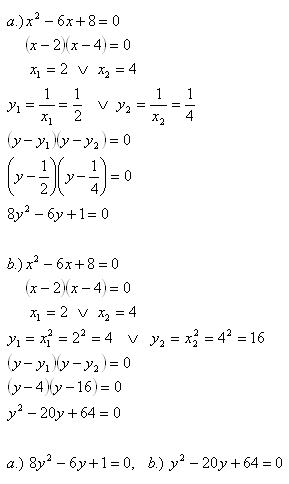
9. Die Gleichung x2–x·cos α + cos 2α = 0 hat die Wurzeln x1 , x2. Drücken Sie den Ausdruck aus:
Lösung:
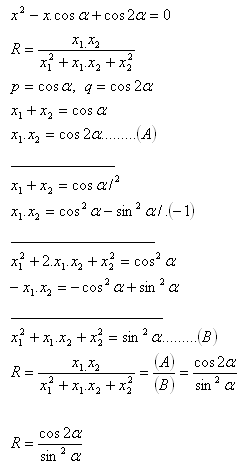
10. Wenn x1 und x2 die Wurzeln der Gleichung 2x2 + 1,1x - 3,91 = 0 sind, berechnen Sie (x1 – x2)2, ohne die Gleichung zu lösen.
Lösung: