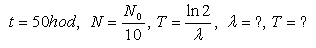Logaritmy - základy
Logaritmus
Logaritmus kladného čísla x při základě a ( a je kladné a nerovná se 1 ) je exponent y, kterým jestli umocníme základ a, dostaneme číslo x.
logax =y lebo ay=x a > 0 a současně a ≠ 1
Vlastnosti logaritmů
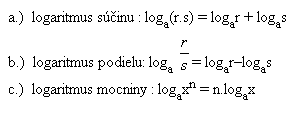
1. Přepište do tvaru logaritmů:
102 = 100 log10 100 = 2
45 =1024 log41024 = 5
130 = 1 log131 = 0
10-3 = 0,001 log100,001 =-3
640,5 =8 log648 = 0,5
5-2 = 0,04 log50,04=-2
2. Vypočítejte a zdůvodněte:
log101000 log101000 = 3 lebo 103 = 1000
log381 log381 = 4 lebo 34 = 81
log20,5 log20,5 =-1 lebo 2-1 = 0,5
log171 log171 = 0 lebo 170 =1
log1111 log1111 = 1 lebo 111 = 11
log50,2 log50,2 = -1 lebo5-1 = 0,2
log150 log150 =nedefinovaný
log5(-25) log5(-25) = nedefinovaný
log0,40,4 log0,40,4 = 1 lebo 0,41 =0,4
log149 log149 = nedefinovaný
3. Určete x:
log2x = 3 x = 23 =8
log10x = -4 x = 10-4 = 0,0001
log16x = 0,5 x =160,5= 4
log20x =1 x = 201=20
log25x = -0,5 x =25-0,5 = 0,2
log0.2487x = 0 x =0,24870 =1
4. Určete a:
loga25 =2 a = 5
loga81 = 4 a = 3
loga100000 =5 a = 10
loga512 = 3 a = 8
loga0,01 = -2 a = 10
loga5 = 0,5 a = 25
loga36 = 2 a = 6
loga64 = 1 a = 64
5. Zlogaritmujte výrazy (při základě a)
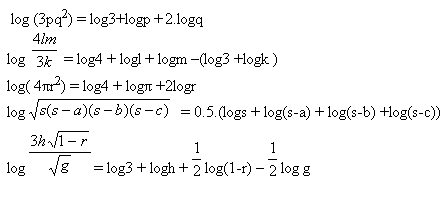
6. Určete číslo x:
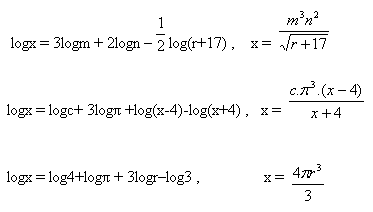
7. Vypočítejte hodnotu výrazu:
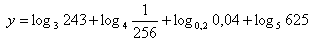
Řešení:
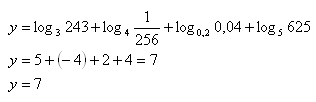
Zdůvodnění:
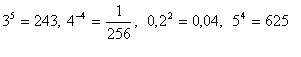
8. Zlogaritmujte výraz (při základě a):
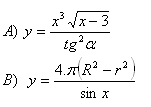
Řešení:
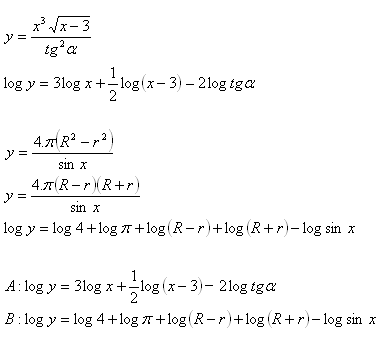
9. Vypočítejte hodnotu výrazu:
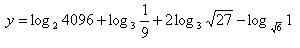
Řešení:
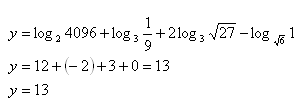
Zdůvodnění:
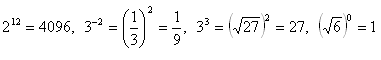
10. Vypočítejte hodnotu výrazu:
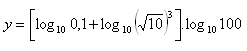
11. Použijte dekadický logaritmus při řešení rovnice:
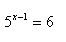
12. Použijte dekadický logaritmus při řešení rovnice:
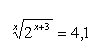
13. Použijte dekadický logaritmus při řešení rovnice:
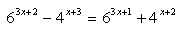
14. Za čas t = 50 hodin klesne aktivita radioaktivního sodíku na desetinu počáteční hodnoty. Jaký je poločas rozpadu tohoto nuklidu? Při výpočtu použijte přirozený logaritmus.