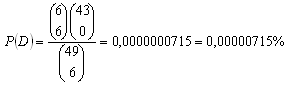Pravděpodobnost
1. Definujte a charakterizujte pravděpodobnost.
Řešení:
a) Klasická definice pravděpodobnosti:
Nechť náhodný pokus splňuje předpoklady
- Počet všech výsledků je konečný
- Všechny výsledky jsou stejně možné
- Žádné dva výsledky nemohou nastat současně
Pravděpodobnost jevu A je číslo
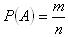
, kde n je počet všech možných výsledků náhodného pokusu am je počet všech příznivých výsledků, tj. výsledků, při kterých nastane jev A..
Platí : 0 ≤ P(A) ≤ 1
Pravděpodobnost nemožného javu : P(A) = 0
Pravděpodobnost jistého javu: P(A) = 1
b) Podmíněná pravděpodobnost A za podmínky B je číslo:
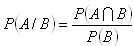 c) Pravděpodobnost nezávislých jevů:
c) Pravděpodobnost nezávislých jevů:
P(A∩B) = P(A)P(B)
d) Pravděpodobnost neslučitelných jevů:
P(AUB) = P(A) + P(B)
e) Binomické rozdělení pravděpodobnosti:
Nechť A je jev s pravděpodobností P. Pak pravděpodobnost, že při n-násobném opakování pokusu, jev A nastane právě k-krát je číslo:
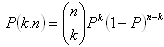 f) Hypergeometrické rozdělení pravděpodobnosti.
f) Hypergeometrické rozdělení pravděpodobnosti.
Nechť V předmětů vybraných z N předmětů má určitou vlastnost, pak NV předmětů tuto vlastnost nemá.
Pravděpodobnost, že právě k předmětů z řad n náhodně vybraných předmětů tuto vlastnost má, je číslo:
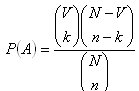
2.Z osmnácti lístků označených čísly 1 - 18 vytáhneme náhodně jeden lístek. Jaká je pravděpodobnost, že na vytažením lístku bude:
a) sudé číslo
b) číslo dělitelné 3
c) prvočíslo
d) dělitelné 6
Řešení:
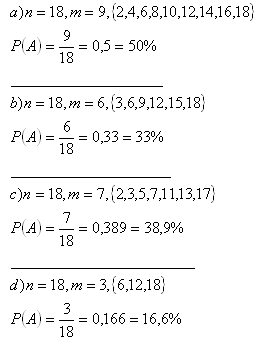
3. Jaká je pravděpodobnost že při hodu dvěma kostkami (červené a modré) padne:
a) součet 8
b) součet, který je děliteľný pěti
c) součet, který bude sudý
Řešení:
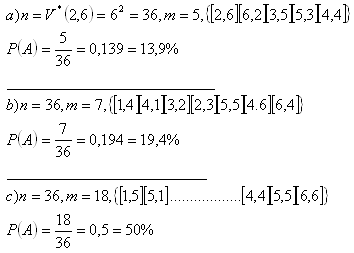
4. Hazardní hráč hází třemi kostkami, položil G. Galileimu otázku: "Mám vsadit na součet 11 nebo součet 12?" Co mu Galilei odpověděl?
Řešení:
a) Součet 11
n = V*(3,6) = 63 = 216
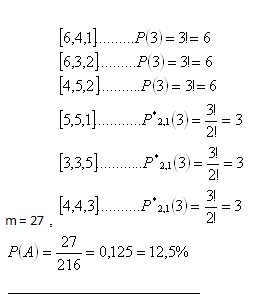
b) Součet 12
n = V*(3,6) = 6
3 = 216
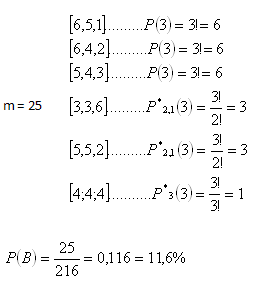
G. Galilei doporučil vsadit na součet 11, protože P (11)> P (12).
5. Dlouhodobé výzkumy na stejném území ukázala, že ze 100 000 dětí se 82 170 dožije 40 let a 37 930 se dožije 70 let. Jaká je pravděpodobnost, že člověk, který se dožije 40 let, dožije se i 70 let?
Řešení:
(Jedná se o podmíněnou pravděpodobnost)
A – dožít se 70 let, P(A) = 0,3793
B – dožít se 40 let, P(B) = 0,8217
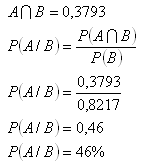
Pravděpodobnost, že se člověk dožije 70 let je 46%.
6. Ve městě jsou čtyři křižovatky se světelnými semafory. Každý z nich uvolňuje nebo uzavírá dopravu se stejnou pravděpodobností 0,5. Jaká je pravděpodobnost, že auto:
a) projde první křižovatkou bez zdržení
b) projde prvními dvěma křižovatkami bez zdržení
c) projde všemi čtyřmi křižovatkami bez zdržení
Řešení:
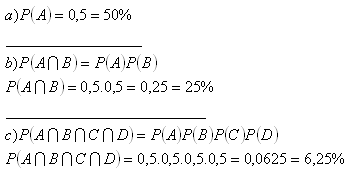
7. V 32 hracích kartách jsou 4 esa a 12 figur (4 králové, 4 horníci a 4 spodci). Jaká je pravděpodobnost, že náhodně vytažena jedna karta bude eso nebo figura?
Řešení:
Jedná se o pravděpodobnost neslučitelných jevů
A – vytažená karta ja eso
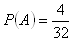
B - vvytažená karta ja figura
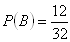
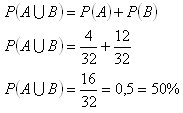
Pravděpodobnost, že vytažená karta bude eso nebo figura je 50%.
8. Otcové jsou šťastní, když se jim narodí syn. Z dlouhodobých statistik je známo, že pravděpodobnost narození chlapce je P (A) = 0,51.
Otec si naplánoval 5 dětí. Jaká je pravděpodobnost, že z těchto dětí budou právě 3 synové.
Řešení:
Jedná se o binomické rozdělení pravděpodobnosti.
n = 5, k = 3, P = 0,51
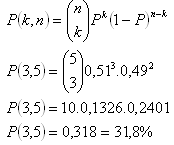
Otci se přání splní s pravděpodobností 31,8%.
9. V šestnácti lahvích jsou minerálky. Víme, že v 10 láhvích je Slatina av 6 lahvích je Baldovská. Jaká je pravděpodobnost, že mezi 4 náhodně vybranými lahvemi jsou 2 Slatiny a 2 Baldovaké?
Řešení:
Jedná se o rozdělení pravděpodobnosti.
N = 16 (počet všech lahví)
V = 10 (počet lahví Slatiny)
N-V = 6 (počet lahví Baldovská)
n = 4 (počet náhodně vybraných lahví)
k = 2 (výběr Slatiny)
n - k = 2 (výběr Baldovská)
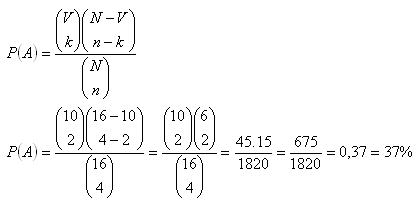
Předpoklad bude splněn s pravděpodobností P (A) = 37%.
10. V hazardnej číselnej hre sa losuje 6 čísiel zo 49 čísiel. Aká je pravdepodobnosť získať:
a) čtvrté pořadí
b) třetí pořadí
c) druhé pořadí
d) první pořadí
Řešení:
a) Čtvrté pořadí (uhodnout 3 čísla ze 6 vylosovaných)
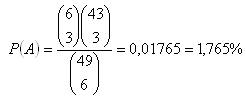
b) Třetí pořadí (uhodnout 4 čísla ze 6 vylosovaných)
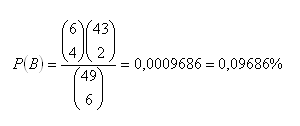
c) Druhé pořadí (uhodnout 5 čísel ze 6 vylosovaných)
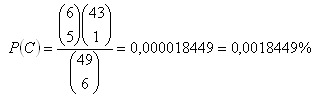
d) První pořadí (uhodnout 6 čísel ze 6 vylosovaných)