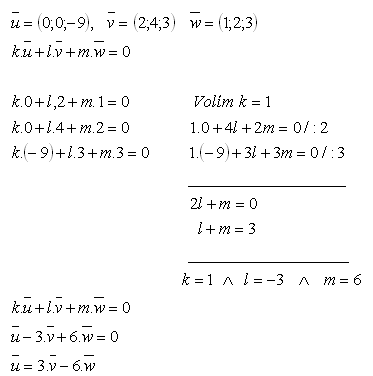Vektor v prostoru
1. Jaké jsou vlastnosti vektoru v prostoru?
Řešení:

2.Zjistěte délku úsečky AB, která má střed S v počátku souřadnicových os a bod A [6; -2; 3]
Řešení:

3.Určete souřadnice vrcholu C [c1; c2; c3] v trojúhelníku Δ ABC, jestliže vrcholy a těžiště mají polohu:
A [3, 3, 3], B [-2; 1; 2], T [0; -1; 0 ]. Zjistěte také obvod tohoto trojúhelníku.
Řešení:
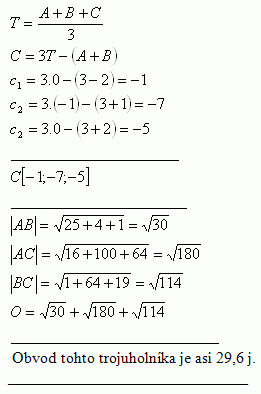
4.Na ose z najděte bod, který je stejně vzdálen od bodů A [-2; 1; 4] a B [3; 0; 1]
Řešení:

5. V rovnoběžnostěnu ABCDEFGH jsou známé souřadnice bodů A [2; -3; 1], B [3; -4; 2], D [4, 2, -3],
E [5; 3; 4]. Vypočtěte souřadnice zbývajících bodů C, F, H, G
Řešení:
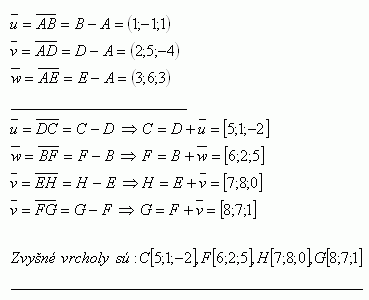
6.Dokažte, že trojúhelník Δ ABC je rovnoramenný a pravoúhlý jestliže: A [2; -4; 9], B [-1; -4; 5], C [6; -4; 6]
Řešení:
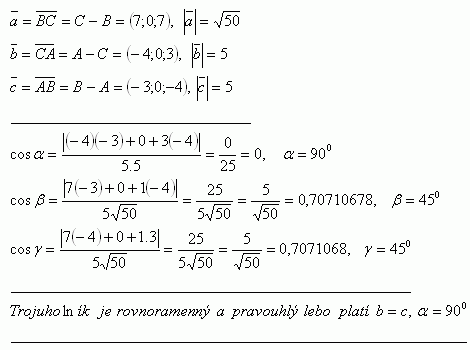
7.Dané jsou vektory:
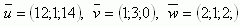
Zjistěte, zda jsou lineárně závislé.
Řešení:

8.Zjistěte, zda dané čtyři body leží v jedné rovině. A[1;2;-1], B[0;1;5], C[-1;2;1], D[2;1;3]
Řešení:

9.Vypočítejte obsah trojúhelníku Δ ABC, jehož vrcholy leží v bodech:
Řešení:

10.Vypočtěte objem čtyřbokého jehlanu ABCDV, pokud znáte jeho vrcholy: A[2;0;0], B[0;3;0], D[0;0;6], V[2;3;8]
Řešení:

11. Určitě délku těžnice v trojúhelníku ABC, jestliže platí: A[1;0;2], B[-2;1;-3], C[0;-1;1].
Řešení:
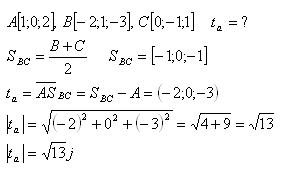
12. Určete vzdálenost středů úseček AB, CD jestliže platí:
Řešení:
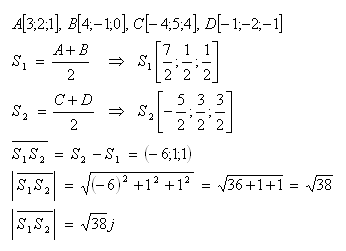
13.Nechť A [1, 2, 8] a B [4; y; 4], pak | AB | = 5. Jaké bude y?
Řešení:

Hľadaný bod je B[4;2;4].
14. Dané jsou body K, L, M, N. Vypočtěte souřadnice bodu N jestliže platí:
Řešení:
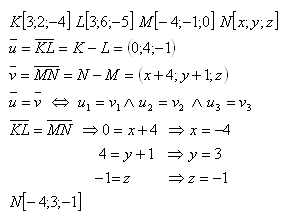
Hledaný bod je N [-4;3;-1].
15.Dané jsou body A [4; -3; 2], B [5; 0; -1]. Určitě čísla m, n tak, aby bod C [2; m; n] ležel na vektoru AB.
Řešení:
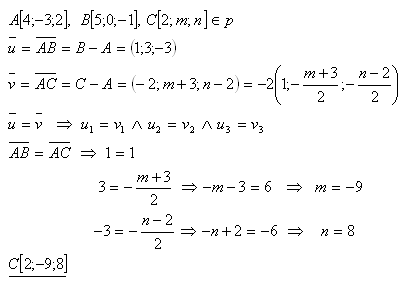
Hledaný bod je C[2;-9;8].
16.Určete vzájemnou polohu vektorů:
Řešení:
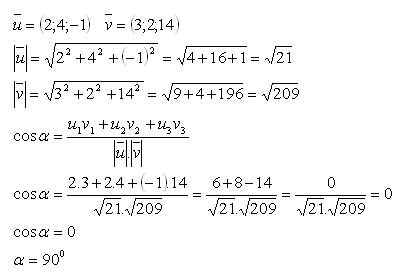
Vektory jsou na sebe kolmé.
17. Dané jsou tři body v prostoru A, B, C. Vypočítejte velikost úhlu
Řešení:
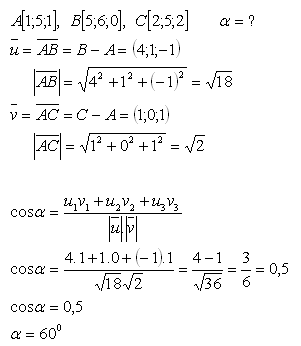
Úhel mezi vektory je α = 600.
18.Vypočítejte obvod a obsah trojúhelníku ABC, jestliže pro jeho vrcholy platí:
A[0;1;2], B[1;2;0], C[2;0;1]
Řešení:
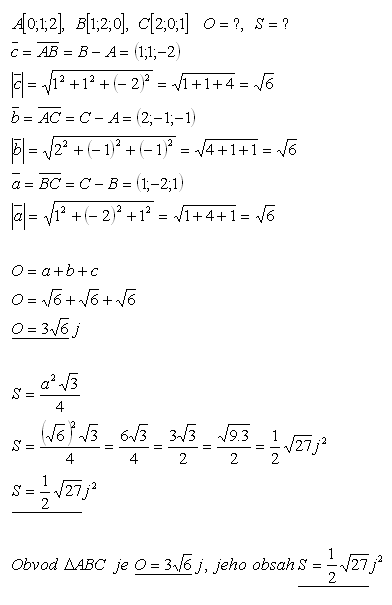
19.V trojúhelníku ABC jsou dány vrcholy A, B a těžiště T. Určitě souřadnice vrcholu C pokud platí:
A[3;3;3], B[-2;1;2], T[0;-1;0], C[x,y,z]
Řešení:
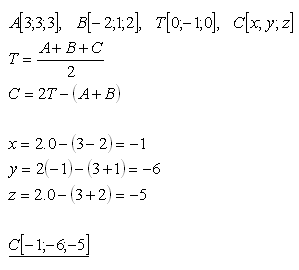
Třetí vrchol ΔABC je C[-1;-6;-5].
20.Vektor u zapište jako lineární kombinaci vektorů vaw jestliže platí:
Řešení: