Trojúhelník
1.Charakterizujte obecný trojúhelník
Riešenie:
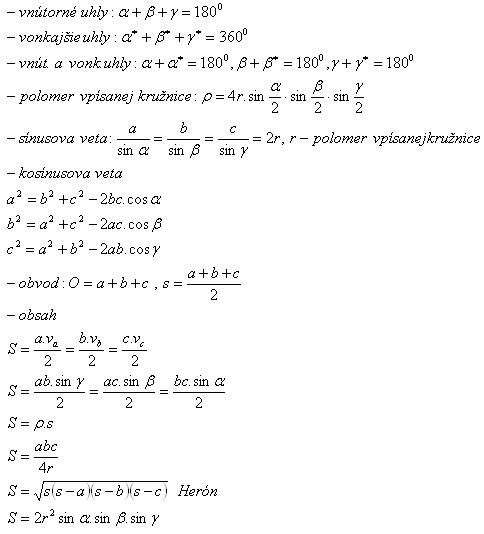
2. Dokažte, že pro vnější úhly trojúhelníku platí α*+ β*+ γ* = 360°.
Důkaz:
α + α* = 180°
β + β* = 180°
γ + γ* = 180°
_____________
α + β + γ + α* + β* + γ* = 540°
α* + β* + γ* = 540° – (α + β + γ)
α* + β* + γ* = 540° - 180°
α* + β* + γ* = 360°
3. Trojúhelník má stranu c = 40 cm. Pro jeho úhly platí: α:β:γ = 3:5:10.
Vypočítejte jeho:
a) obvod
b) obsah
Rešení:
Obvod:
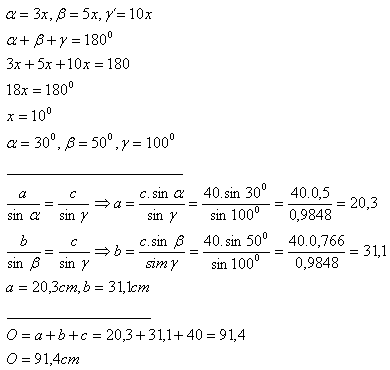
Obsah:
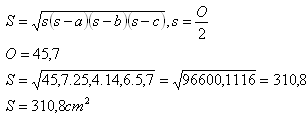
4.Je dán rovnostranný trojúhelník se stranou a = 10 cm.
Vypočítejte obsah plochy mezi kružnicí tomuto trojúhelníku opsanou a vepsanou.
Rešení:
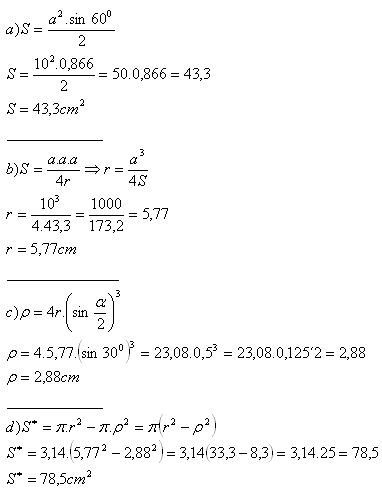
5. Honza je od jednoho konce na zemi ležícího stromu vzdálený 5 m, od druhého 8m. Strom vidí pod zorným úhlem 60°.
Jakou délku má strom?
Rešení:
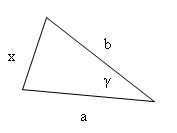
a = 5 m
b = 8 m
γ = 60°
x
2 = a
2 + b
2 -2ab.cosγ
x
2 = 5
2 + 8
2 -2.5.8.cos60°
x
2 = 25 + 64 – 80.0,5
x
2 = 25 + 64 – 40
x
2 = 49
x = 7
Strom je dlouhý 7 m.
6. Tři kružnice s poloměry r1 = 2 cm, r2 = 3cm, r3 = 4cm majú venkovní dotyk.
Vypočítejte vnitřní úhly trojúhelníku, který vznikne pospojování středů těchto kružnic.
Rešení:
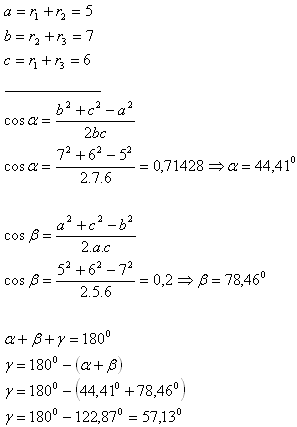
V trojúhelníku jsou úhly α = 44,41°, β = 78,46° a γ = 57,13°.
7.Ze stanice současně vyšly dva vlaky na přímých tratích pod úhelem φ = 156°
rychlostmi v1 = 13 ms-1, v2 = 14,5 ms-1.
Jak jsou od sebe vzdáleny za čas t = 5 min?
Rešení:
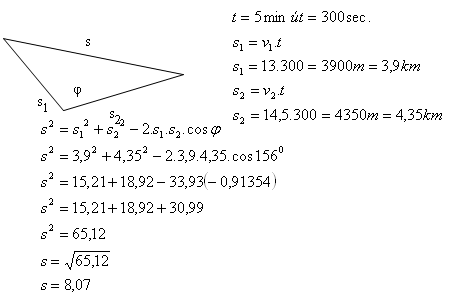
Vlaky po pěti minutách budou od sebe vzdáleny asi 8 km.
8. Síly F1, F2 mají společné působiště a svírají úhel φ = 60°.
- Jak velká je jejich výslednice, ak F1 = 42N, F2 = 35N.
- Určete úhly, které svírají sily F1, F2 s výslednicou.
Rešení:
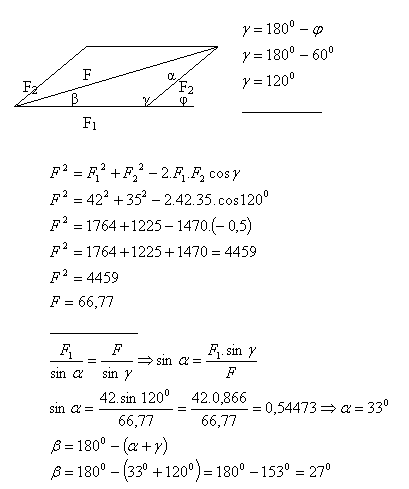
- Výslednice sil je F = 66,77N.
- Úhly pro výslednici F s F1 a F2 jsou α = 33° a β = 27°.
9. Z věže vysoké 20 ma vzdálené od řeky 20 m se jeví šířka řeky pod úhlem 15°.
Jaká široká je řeka v tomto místě?
Rešení:
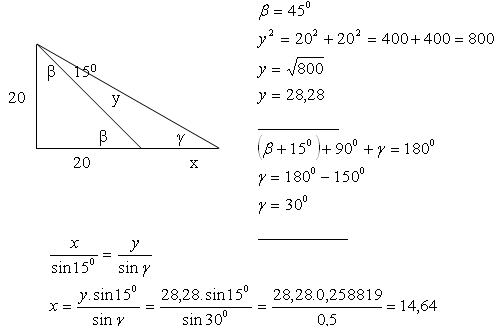
Šířka řeky na tomto místě je x = 14,64 m.
10. Těleso, které má hmotnost m = 1563 kg je zavěšeno na vodorovném trámu na dvou lanech různé délky. Lana svírají s šířkou úhly α = 48°, β = 62°.
Vypočítejte namáhání lan v tahu. (F = 15630 N)
Rešení:
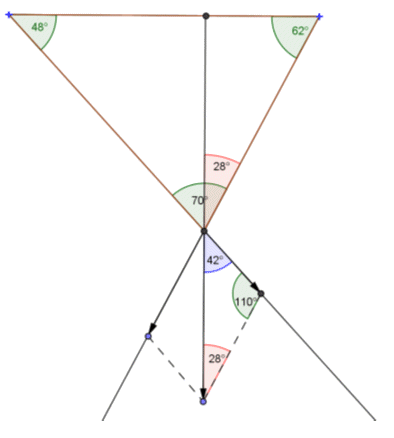
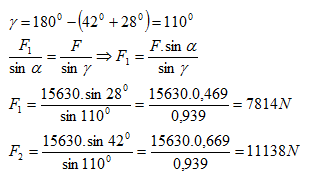
Lana jsou namáhány silami F1 = 7814 N a F2 = 7814 N.