Permutácie
1. Definujte a charakterizujte:
a) Permutácie z n prvkov
b) Permutácie z n prvkov s opakovaním
Riešenie:
Permutácie
Permutácia n prvkov je každá usporiadaná n –tica vytvorená z týchto prvkov.
Každý z n prvkov sa v tejto n-tici vyskytuje práve raz. Jednotlivé permutácie sa od seba líšia len poradím prvkov.
P(n) = n!
Permutácie s opakovaním
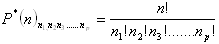
n
1 – počet rovnakých prvkov 1.druhu
n
2 - počet rovnakých prvkov 2.druhu
n
3 - počet rovnakých prvkov 3. druhu atď
n
j - počet rovnakých prvkov j-tého druhu
Platí : n
1+n
2+n
3+.........+n
j = n
2. Dané sú tri prvky a, b, c. Vytvorte z nich::
a) permutácie (bez opakovania)
b) permutácie s opakovaním, v ktorých sa „ a“ vyskytne 2 krát,“ b“ raz a „c“ raz
Riešenie:
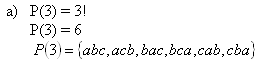
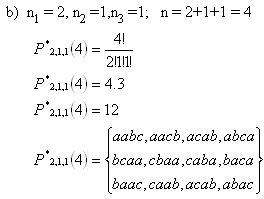
3. Koľko rôznych päťciferných prirodzených čísiel možno napísať pomocou číslic 1,2,3,4,5, ak:
a) číslica sa v čísle použije len raz?
b) Koľko z napísaných čísiel sa bude začínať číslicou 5?
c) Koľko z napísaných čísiel bude párnych?
Riešenie:
a) P(5) = 5! = 5.4.3.2.1 = 120
b) P(4) = 4! = 4.3.2.1 =24
c)
končiacich 2: P(4) = 4! =24
končiacich 4: P(4) = 4! = 24
spolu : S = 2.4! = 2.24 = 48
4. Osem študentov má na internáte pripravené ubytovanie v troch izbách. Dve sú trojpostelové a jedna dvojpostelová. Koľko je spôsobov rozdelenia študentov do izieb?
Riešenie:
Prvá izba: n1 = 3
Druhá izba: n2 = 3
Tretia izba: n3 = 2
n = 3 + 3 + 2 = 8
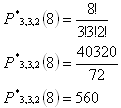
Existuje 560 spôsobov rozdelenia študentov do izieb.
5. Koľkorakým spôsobom je možné hodiť troma kockami súčet 11?
Riešenie:
a) permutácia trojice 6,4,1 : P(3) = 3! = 6
b) permutácia trojice 6,3,2 : P(3) = 3! = 6
c) permutácia trojice 5,5,1 : P2,1*(3) = 3
d) permutácia trojice 5,4,2 : P(3) = 3! = 6
e) permutácia trojice 5,3,3 : P*1,2(3) = 3
f) permutácia trojice 4,4,3 : P*2,1(3) = 3
Spolu 6+6+3+6+3+3 = 27 spôsobov.
6. Štyri české a tri slovenské knihy treba usporiadať na poličke tak, aby boli zoradené najprv české a potom slovenské knihy. Koľkorakým spôsobom sa to dá urobiť?
Riešenie:
Usporiadanie českých kníh: P(4) = 4! =24
Usporiadanie slovenských kníh: P(3) = 3! = 6
N = P(4).P(3) = 24.6 = 144
Knihy sa dajú usporiadať 144 spôsobmi.
7. Ak sa zväčší počet prvkov o 2, zväčší sa počet permutácií (bez opakovania) 42 krát.
Koľko prvkov na to potrebujeme?
Riešenie:
P(x + 2) = 42.P(x)
(x + 2)! = 42.x!
(x + 2)(x +1)x! = 42x!/: x!
(x + 2)(x + 1) = 42
x2 + 3x +2 - 42 = 0
x2 +3x – 40 = 0
(x – 5)(x + 8) = 0
x1 = 5
x2 = - 8 nevyhovuje
K={5}
Potrebujeme 5 prvkov.
8. Pätnásti svadobčania sa nemohli dohodnúť, kto kde bude stáť na svadobnej fotografii.
Ženích navrhol, aby sa urobili všetky možné zostavy svadobčanov na fotografiách.
- a) Koľko fotografií treba urobiť?
- b) Koľko by fotografovanie trvalo, keby vyfotografovanie jednej fotky trvalo 10 sekúnd a fotografovalo by sa deň aj noc?
Riešenie:
a)
P(15) = 15! = 1,307.10
12
Treba urobiť 1,307.10
12 fotografií.
b)
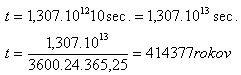
Fotografovanie by trvalo 414 377 rokov.
9. Šesťciferný kód uzatvárania trezoru v banke je vytvorený z tých istých číslic ako číslo 926002.
Koľko je možností vytvorenia príslušného kódu?
Aký čas by trvalo zlodejovi vytočiť všetky možnosti, ak vytočiť jeden kód mu trvá 5 sekúnd?
Riešenie:
n
1 = 2, n
2 = 2, n
3 = 1, n
4 = 1, n = 6
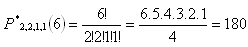
t = 180.5sec. = 900 sec. = 15 minút
Možností je 180 a zlodejovi by to trvalo 15 minút (ak správny je až posledný vytočený kód).
10. Študent, ktorý sa hlási na vysokú školu musí urobiť 4 skúšky. Za každú úspešne urobenú skúšku dostane podľa obťažnosti 2,3 alebo 4 body. Na prijatie stačí dosiahnuť 13 bodov. Koľkými spôsobmi môže študent urobiť skúšky, aby bol prijatý?
Riešenie:
Aby bol študent prijatý musí získať 13, 14, 15 alebo 16 bodov.
| 13 bodov: |
(3,3,3,4) |
P*3,1(4) = 4 |
| |
(4,4,3,2) |
P*2,1,1(4) = 12 |
| 14 bodov: |
(4,4,4,2) |
P*3,1(4) = 4 |
| |
(4,4,3,3) |
P*2,2(4) = 6 |
| 15 bodov: |
(4,4,4,3) |
P*3,1(4) = 4 |
| 16 bodov: |
(4,4,4,4) |
P*4(4) = 1 |
N = 4 + 12 + 4 + 6 + 4 + 1 = 31
Študent má spolu 31 možností ako získať požadované body.