Kocka, kváder, hranol a valec
1. Uveďte základné vzťahy pre výpočet objemu a povrchu:
- kocky
- kvádra
- hranola
- valca
Riešenie:
Kocka
a – hrana kocky
objem V = a
3
obsah S = 6a
2
 Kváder
Kváder
a, b, c – hrany kvádra
objem V = a.b.c
obsah S = 2(ab+ac+bc)
 Hranol
Hranol
S
p – obsah podstavy
Q – obsah plášťa
v – výška hranola
objem V = S
p.v
obsah S = 2S
p + Q
Valec
r – polomer podstavy
v – výška valca
objem V = π.r
2.v
obsah S = 2πr(r+v)
Q = 2πrv
2. Dve debničky tvaru kocky s hranami a = 70 cm, b = 90 cm treba nahradiť jednou debničkou tvaru kocky.
Aká bude jej hrana?
Riešenie:
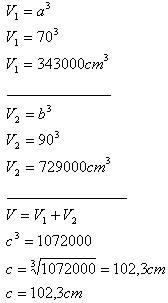
Hrana náhradnej kocky bude c = 102,3 cm.
3. Hrana druhej kocky je o 2 cm väčšia, ako hrana prvej kocky. Rozdiel objemov kociek je 728 cm3.
Vypočítajte veľkosti hrán obidvoch kociek.
Riešenie:
Hrana prvej kocky: x
Hrana druhej kocky: x + 2
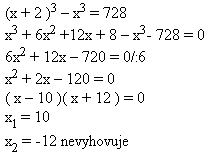
Hrana prvej kocky je 10 cm, druhej 12 cm.
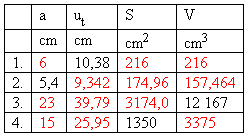
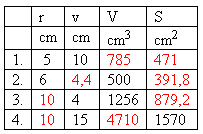
4. Daná je kocka o hrane a. Známe hodnoty sú v tabuľke.
Doplňte tabuľku!
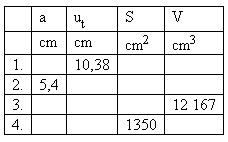
Riešenie:
5. Hrany dvoch kociek sa líšia o 22 cm. Ich povrchy sa líšia o 19272 cm2.
Určite hrany obidvoch kociek.
Riešenie:
x – hrana prvej kocky
y – hrana druhej kocky
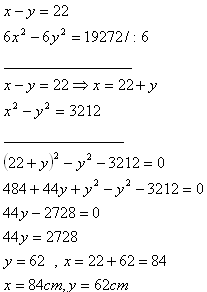
Hrany kociek sú x = 84 cm a y = 62 cm.
6. Kváder má rozmery a = 4 cm, b = 3 cm, c = 5 cm.
Vypočítajte uhol α medzi podstavovou a telesovou uhlopriečkou.
Riešenie:
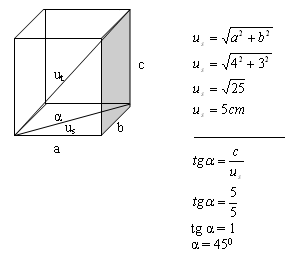
Uhol medzi uhlopriečkami je α = 45°.
7. Povrch kvádra je S = 376 cm2. Pre jeho hrany platí a:b:c = 3:4:5.
Vypočítajte objem tohto kvádra.
Riešenie:
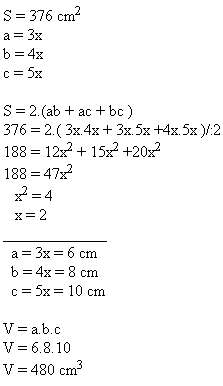
Objem kvádra je V = 480 cm
3.
8. Vo vodojeme tvaru kvádra je 1500 hl vody, výška vody je 2,5 m.
Určite rozmery dna, ak jeden rozmer je o 4 m väčší, ako druhý.
Riešenie:
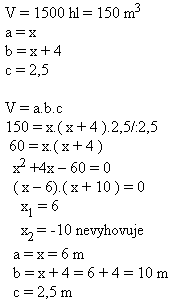
Rozmery dna vodojemu sú a = 6 m, b = 10 m.
9. Vypočítajte objem kvádra, ak jeho podstava má S1 = 272 cm2 a bočné steny S2 = 240 cm2, S3 = 255 cm2.
Riešenie:
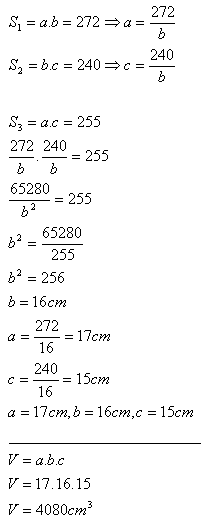
Objem kvádra je 4080 cm
3.
10. Akú hmotnosť má železná tyč (ρ = 7800 kg.m-3) 1,5 metrov dlhá, ktorej prierezom je štvorec so stranou a = 45 mm?
Riešenie:
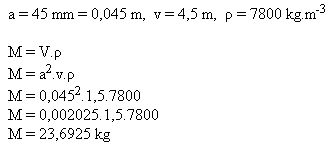
Hmotnosť železnej tyče je asi M = 23,7 kg.
11. Podstava kolmého trojbokého hranola je pravouhlý trojuholník s odvesnami a = 9 cm, b = 12 cm. Výška hranola je dvojnásobok prepony pravouhlej podstavy hranola.
Vypočítajte objem a povrch hranola.
Riešenie:
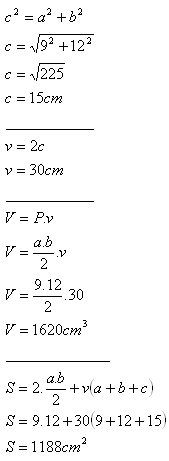
Trojboký hranol má objem V = 1620 cm
3 a povrch S = 1188 cm
2.
12. Koľko zeminy treba premiestniť pri výkope priamej 170 m dlhej priekopy, ktorej prierez je rovnoramenný lichobežník so základňami a = 150 cm, c = 80 cm a výškou v = 83 cm?
Riešenie:
l = 170 m = 17000 cm
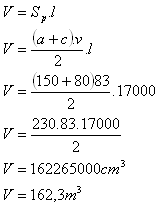
Treba premiestniť asi 162,3m
3 zeminy.
13. Vypočítate objem a povrch hranola, ktorého podstava je kosoštvorec s uhlopriečkami u1 = 12 cm, u2 = 16 cm. Výška hranola sa rovná dvojnásobku podstavovej hrany.
Riešenie:
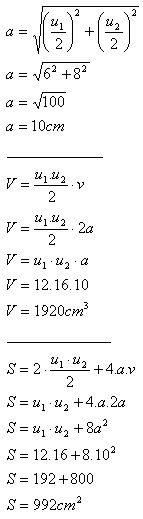
Objem hranola je V = 1920 cm
3, jeho povrch je S = 992 cm
2.
14. V tabuľke sú veličiny charakterizujúce rôzne valce.
Doplňte tabuľku!
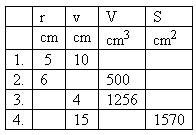
Riešenie:
15. Plášť rotačného valca rozvinutý do roviny je štvorec s obsahom a2 = 81 cm2.
Určite polomer podstavy r, výšku valca v a jeho objem V.
Riešenie:
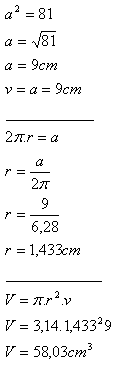
Valec má polomer podstavy r = 1,433 cm, výšku v = 9 cm a objem V = 58,03 cm
3.
16. Rovnostranný valec (v = 2r) má objem V = 250 cm3.
Vypočítajte povrch tohto telesa.
Riešenie:
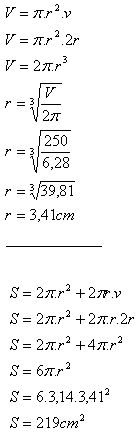
Povrch tohto valca je S = 219 cm
2.
17. Hliníkový drôt (ρ = 2,7 g.cm-3) s priemerom d = 3 mm má celkovú hmotnosť m = 1,909 kg.
Určite dĺžku drôtu l.
Riešenie:
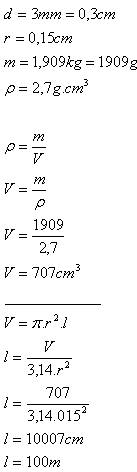
Dĺžka hliníkového drôtu je približne 100m.
18. Vonkajší obvod mosadznej rúrky (ρ = 8,5 g.cm-3) je 31,4 cm. Jej hmotnosť je 3,14 kg a dĺžka je 60 cm.
Aká je hrúbka steny rúrky?
Riešenie:
O = 31,4 cm
v = 60 cm
m = 3140 kg
ρ = 8,5 kg.cm
-3
hrúbka rúrky = x
V úlohe ide o objem dutého valca s podstavou medzikružia.
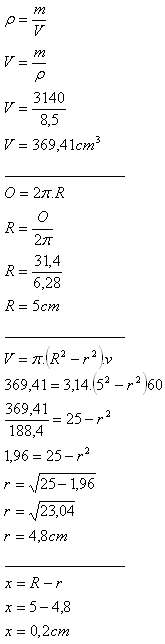
Hrúbka steny rúrky je x = 0,2 cm.