Ludolfovo číslo v stredovekej Európe
V stredoveku v Západorímskej ríši i vo Východorímskej Byzantskej ríši neexistovali podmienky pre vedeckú prácu v prírodných vedách a v matematike. Ľudia zaoberajúci sa matematikou boli nazývaní podvodníkmi, šarlatánmi, kacírmi. Byzantský cisár Justián (527 – 565) umiestnil v zbierke zákonov časť nazvanú „O zločincoch, matematikoch a im podobných“ a v nej paragraf „Matematika ako umenie odsúdeniahodné sa čo najprísnejšie zakazuje“. Na inom mieste sa vyhráža prísnymi trestami pre každého „kto sa bude radiť s veštcom alebo matematikom“. Zaznela aj veta: „Vie deliť veľké čísla, zapredal dušu diablovi. Patrí katovi“. Preto sa nemôžeme diviť, že matematika tohto obdobia bola na veľmi nízkej úrovni.
Napriek všetkému nezáujmu, nepochopeniu a prenasledovaniu objavili sa v stredoveku na matematickom nebi dve jasné hviezdy: Leonardo Pisánsky (Fibonnacci) a Johannes Müller(Regiomontánus).
L. Pisánsky (1170 – 1240) v roku 1202 napísal svoju najznámejšiu prácu „Liber abaci“ a v roku 1220 prácu „Prax geometrie“. Uvádza v nej nerovnosť:
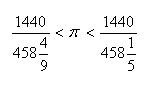
Pre výpočet použil aritmetický priemer dolnej a hornej aproximácie
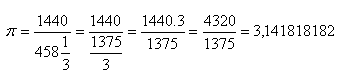
J.Müller (1436 – 1476) určil číslo π pomocou funkcie sínus a tabuliek, ktoré zostavil. Použil kružnicu s polomerom r = 6.106. Zistil, že tetiva prislúchajúca na tejto kružnici stredovému uhlu α = 10 je dlhá t = r.sinα
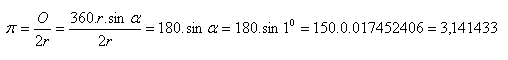
J. Müller – Regiomontánus pôsobil v Košiciach a na Academii Istropolitana v Bratislave.