Ihlan a kužeľ
1. Charakterizujte výpočet objemu a obsahu pre:
- ihlan
- zrezaný ihlan
- kužeľ
- zrezaný kužeľ
Riešenie:

2. Daný je pravidelný štvorboký ihlan (podstava je štvorec o strane a).
Doplňte chýbajúce hodnoty tabuľky.
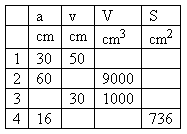
Riešenie:
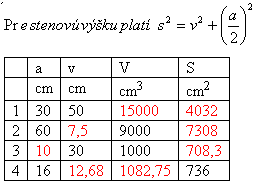
3. Nad každou stenou kocky s hranou a = 30 cm je zostrojený pravidelný štvorboký ihlan s výškou 15 cm.
Vypočítajte objem takto vzniknutého telesa, ak vrcholy ihlanov:
a) ležia mimo kocky
b) ležia vo vnútri kocky
Riešenie:
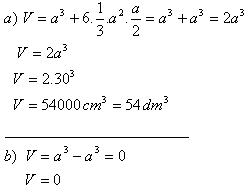
Objem telesa v prvom prípade je V = 54 dm
3, v druhom prípade je nulový.
4. Vypočítajte objem ihlana, ktorého bočná hrana dĺžky 5 cm zviera so štvorcovou podstavou uhol α = 60°. (Uhol α je uhol medzi hranou a uhlopriečkou podstavy.)
Riešenie:
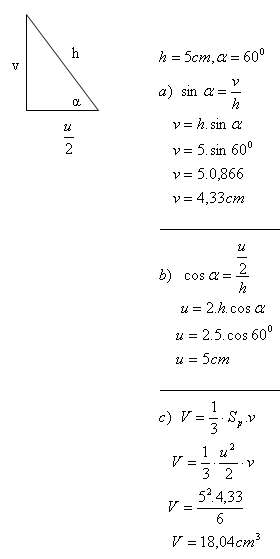
Objem ihlana je V = 18,04 cm
3.
5. Určite hmotnosť betónového piliera (ρ = 2,2 g.cm-3) tvaru pravidelného štvorbokého zrezaného ihlana, ak jeho štvorcové postavy majú strany a = 45 cm, b = 25cm a výška piliera je v = 33 cm.
Riešenie:
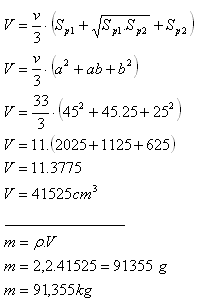
Hmotnosť betónového piliera je m = 91,355 kg.
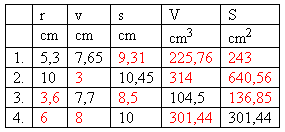
6. Daný je kužeľ s rozmermi uvedenými v tabuľke.
Doplňte tabuľku.

Riešenie:
7. Pravouhlý trojuholník s odvesnami a = 3 cm, b = 4 cm rotuje okolo dlhšej odvesny.
Vypočítajte objem a povrch takto vzniknutého kužeľa.
Riešenie:
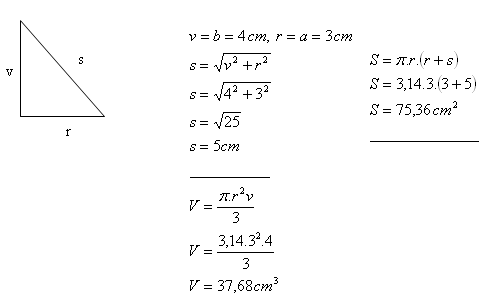
Kužeľ má objem V = 37,68 cm
3 a povrch S = 75,36 cm
2.
8. Povrch kužeľa je S = 235,5 cm2. Osový rez kužeľom je rovnostranný trojuholník.
Vypočítajte objem kužeľa.
Riešenie:
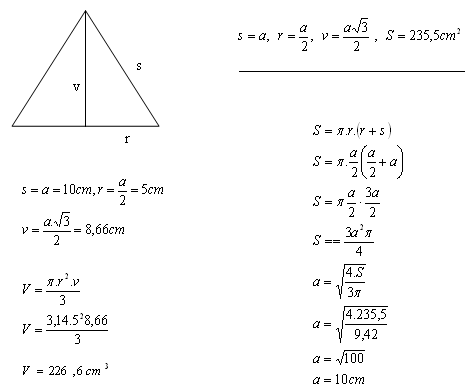
Objem kužeľa je 226,6 cm
3.
9. Plášť kužeľa rozvinutý do roviny má tvar kruhového výseku so stredovým uhlom α = 150° a obsahom S = 523,4 cm2.
Vypočítajte rozmery tohto kužeľa a jeho objem.
Riešenie:
S = 523,4cm
2 - obsah kruhového výseku s polomerom R - obsah plášťa s polomerom r
o = R. arcα - kružnicový oblúk prislúchajúci výseku
O = 2π.r - dĺžka podstavovej kružnice kužeľa
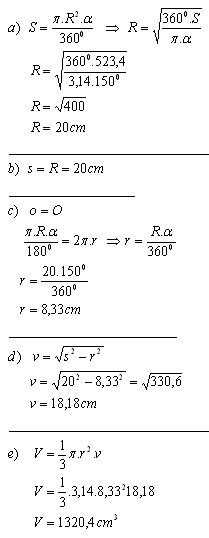
Rozmery kužeľa sú r = 8,33 cm, s = 20 cm, v = 18,18 cm a objem V = 1320,4 cm
3.
10. Povrch zrezaného kužeľa je 7693 cm2, polomery podstáv sú 28 cm a 21 cm.
Vypočítajte výšku kužeľa a jeho objem.
Riešenie:
S = 7693 cm
2
R = 28 cm
r = 21 cm
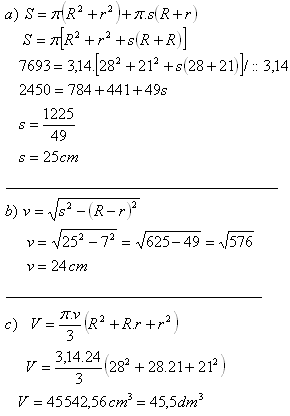
Výška kužeľa je v = 24 cm, jeho objem V = 45,5 dm
3.
11. Objem zrezaného kužeľa je V = 38 000π cm3. Polomer dolnej podstavy je o 10 cm väčší, ako polomer hornej podstavy.
Určite polomery podstáv, ak v = 60 cm.
Riešenie:
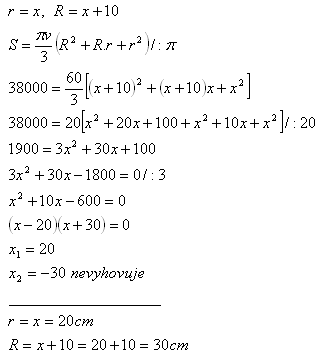
Polomery podstáv zrezaného kužeľa sú R = 30 cm a r = 20 cm.
12. Zrezaný kužeľ s polomermi x = 15 cm, y = 13 cm a výškou v = 9 cm rozvalcovali na valec s polomerom r = 7,67 cm.
Aká je dĺžka tohto valca?
Riešenie:
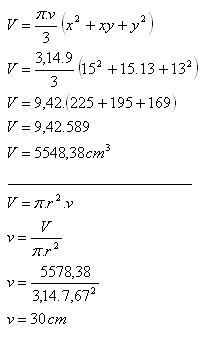
Dĺžka / výška valca je 30 cm.