Special theory of relativity

1. Explain the difference between classical physics and the special theory of relativity,

Solution:

Classical physics (Archimedes, Newton) studies the physical properties of bodies that are relatively large and move at low speeds (v << c). It considers mass, length, time, simultaneity of two events, momentum, and energy as constant, independent of the speed of motion.

The special theory of relativity (Einstein) studies the motion of bodies that move at speeds comparable to the speed of light in a vacuum c.

special-relativity-1

2. From an electron source, two electrons fly out in opposite directions. Each electron has a speed v₁ = v₂ = 0.8c relative to this gun. What is their relative speed?

Solution:

Analysis:

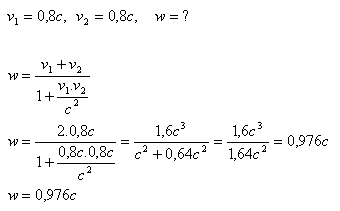
The relative speed of the electrons is w = 0.976c.

3. An α particle flew out of a laboratory accelerator with speed v and moved uniformly in a straight line. It passed through a tube of length 12 cm in 10 ns. What is the length of the tube in the reference frame attached to the α particle?

Solution:

Analysis:

s = 12 cm = 0.12 m, t = 10 ns = 10^-9s, l = ?

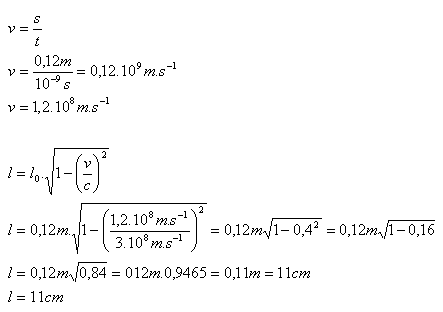
The length of the accelerator tube contracted to 11 cm.

4. A beam of π mesons flies out of an accelerator at speed v = 0.8c. The half-life of π mesons is t₀ = 1.8·10^-8s. Calculate the time it takes for half of the mesons to decay and the distance they travel before decaying.

Solution:

Analysis:

v = 0.8c, t₀ = 1.8·10^-8s, t = ?, s = ?

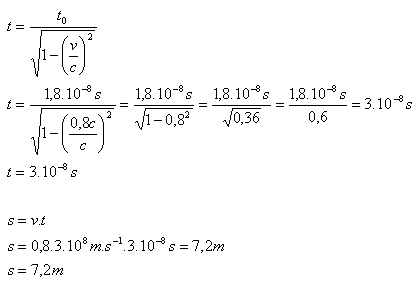
Half of the mesons decay after t = 3·10^–8s. During this time they travel a distance s = 7.2 m.

5. The density of iron is ρ₀ = 7400 kg·m^-3 in the rest frame. How does the density of an iron body change if its speed increases from zero to v = 0.5c?

Solution:

Analysis:

ρ₀ = 7400 kg·m^-3, v = 0.5c, ρ = ?

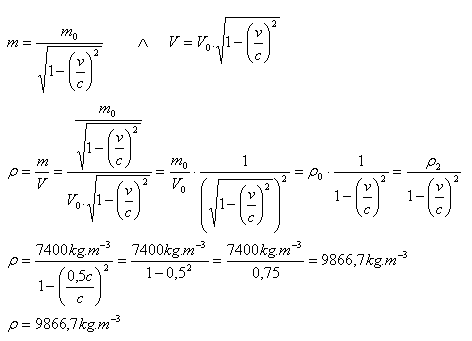
The density of the body changes to ρ = 9866.7 kg·m^-3.

6. Calculate the speed at which the relativistic momentum of an α particle is twice as large as the momentum calculated according to the rules of classical mechanics.

Solution:

Analysis:

2p₀ = p

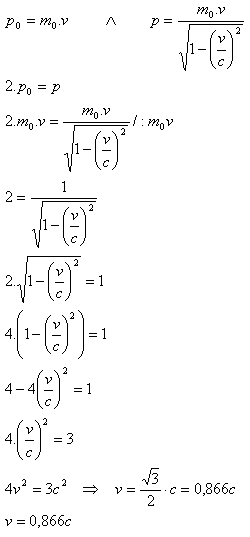
The speed of the α particle is v = 0.866c

7. A spaceship moves relative to Earth at a speed of 12,000 km·s^-1. How long does an event that lasts 1 hour on Earth take for an observer in the spaceship?

Solution:

Analysis:

v = 12,000 km·s^-1 = 1.2·10⁷ m·s^-1, t₀ = 1 hour, t = ?

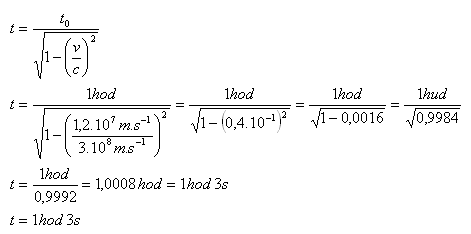
For the observer in the spaceship, the event lasts about 1 hour and 3 seconds.

8. What is the wavelength of a photon whose energy equals the energy of an electron moving at v = 0.6c?

Solution:

Analysis:

v = 0.6c, c = 3·10⁸ m·s^-1, h = 6.625·10^-34 J·s, m_e = 9.1·10^-31 kg, λ = ?,

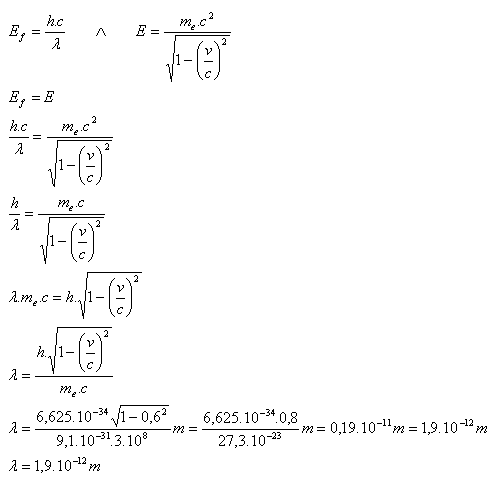
The wavelength of the photon is λ = 1.9·10^-12 m.

9.The star is approaching Earth with speed v. At what speed does the light from this star travel through space for an observer on Earth?

Solution:

The light from this star travels through space for an observer on Earth at speed w = c = 3·10⁸ m·s^–1.

10.In a “cosmic train” moving through space with speed v₁ = c/2, an astronaut moves with speed v₂ = c/4 along the “train”. What speed will an observer standing outside the “train” measure if the astronaut moves

a.) in the same direction as the “train”
b.) in the opposite direction to the “train”

Solution:

The observer standing outside the “train” will measure speeds of 2c/3 or 2c/7.

11.A hyperon moves in a bubble chamber with speed v₁ = 0.8c and, when decaying into a proton, electron, and antineutrino, emits in the direction of its motion a proton that in the rest frame of the hyperon moves with speed v₂ = 0.3c. What speed will the proton have with respect to the coordinate system of the bubble chamber if

a.) the relativistic velocity-addition formula does not apply
b.) the relativistic velocity-addition formula does apply

Solution:

The proton will move at speed 0.887c.

The speed 1.1c > c does not exist.

12.A school lesson on Earth lasts 45 minutes. How many minutes would the lesson last on a spacecraft, from the perspective of an observer on Earth, if the spacecraft is receding from Earth with speed v = 0.6c?

Solution:

The lesson on the spacecraft would last 56 minutes and 15 seconds from the perspective of the observer on Earth.

13.What speed must a rocket have relative to Earth so that a certain process observed on Earth is observed by the astronaut in the rocket as twice as long?

Solution:

The rocket must have speed v = 0.866c.

14.The mean lifetime of a meson is Δt₀ = 2.2·10^–6 s. Calculate the distance the meson travels from its creation to its decay into an electron and neutrino. The meson moves with speed v = 0.96c.

Solution:

During its lifetime the meson travels a distance of about 2.3 km.

15.The distance of the star Proxima Centauri from Earth is 4.28 ly (light-years). What distance will be measured by an observer in a spacecraft that travels from Earth to the star with speed v = 0.8c relative to Earth?

Solution:

The observer in the spacecraft will measure the distance to the star as l = 2.568 ly. That is 24.3·10¹⁵ meters.

16.A body that has the shape of a cube in its rest frame moves uniformly in the direction of the x-axis with speed v = 0.95c perpendicular to a face of the cube. The rest length of the cube is a₀ = 1 m. Determine the volume of the body in the frame with respect to which the body is moving.

Solution:

The volume of the body moving with speed 0.95c is V = 0.312 m³.

17.What was the rest length of a rod that moves relative to an observer at rest with speed v = 2.7·10⁸ m·s^–1? The observer sees the rod as 2.61 m long.

Solution:

The rest length of the rod was l₀ = 6 meters.

18.An elementary particle moves with speed v = 0.8c. What is the ratio of its mass to its rest mass?

Solution:

The ratio of the masses of the elementary particle is m : m₀ = 5 : 3.

19.An electron has been accelerated by a cyclotron so that its relativistic mass has become 5 times larger than its rest mass. What speed does the electron have?

Solution: