sk|cz|en|

Physik

Stoffeigenschaften

1.Welche physikalischen Größen charakterisieren einen Stoff?

Lösung:

Atom AZX

  • – Protonenzahl (Anzahl der Protonen im Kern, Anzahl der Elektronen in der Hülle, Ordnungszahl des Elements im Periodensystem nach Mendelejew)

  • A – Nukleonenzahl (Anzahl der Protonen und Neutronen im Kern)

  • N=A−ZN = A - Z – Anzahl der Neutronen im Kern

ma(X) = Ruhemasse des Atoms(ma(612C)=1.9926×10−26 kg)m_a(X) \,=\, \text{Ruhemasse des Atoms} \quad (m_a(^{12}_{6}C) = 1.9926 \times 10^{-26} \, \text{kg})mu=atomare Masseneinheitmu=112ma(612C)=1.6605×10−27 kgm_u = \text{atomare Masseneinheit} \quad m_u = \tfrac{1}{12} m_a(^{12}_{6}C) = 1.6605 \times 10^{-27} \, \text{kg}

Relative Atommasse

Ar=mamuA_r = \frac{m_a}{m

Relative Molekülmasse

Mr=MmmuM_r = \frac{M_m}{m_u}

Stoffmenge nn – charakterisiert einen Stoff anhand der Anzahl der darin enthaltenen Teilchen

n=NNA,[n]=1 moln = \frac{N}{N_A}, \quad [n] = 1 \, \text{mol}

1 mol – die Einheit der Stoffmenge. Ein Mol ist auch die Stoffmenge, die ebenso viele Teilchen enthält, wie Atome in 0.012 kg0.012 \, \text{kg} von 612C{}^{12}_{6}C.

Avogadro-Konstante:

NA=6.022×1023 mol−1(Anzahl der Teilchen in 1 mol Stoff)N_A = 6.022 \times 10^{23} \, \text{mol}^{-1} \quad (\text{Anzahl der Teilchen in 1 mol Stoff})

Molmasse:

M=mn=Mr⋅10−3,[M]=kg.mol−1M = \frac{m}{n} = M_r \cdot 10^{-3}, \quad [M] = \text{kg·mol}^{-1}

Molvolumen:

Vm=Vn,[Vm]=m3⋅mol−1V_m = \frac{V}{n}, \quad [V_m] = \text{m}^3 \cdot \text{mol}^{-1}

 

2.Bestimmen Sie die Ruhemasse der Atome der Elemente H, C, Zn. Wie groß ist die relative Masse von Uran, wenn seine Ruhemasse ma(U) = 3.95·10-25 kg ist. Verwenden Sie Tabellen.

Lösung:

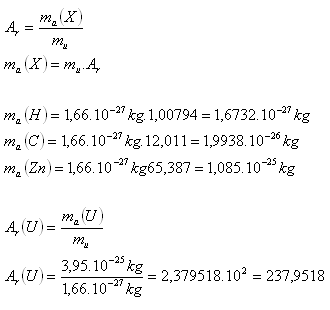
 physics-substance-characteristics-2.gif

Die relative Masse von Uran ist näherungsweise Ar(U) = 238

3.Schätzen Sie die ungefähre Anzahl der Atome in einem Eisen-Gewicht mit der Masse 1 kg. Wie lang wäre eine Linie, wenn all diese Atome dicht aneinandergereiht in einer einzigen Geraden lägen? Der Durchmesser eines Atoms beträgt etwa 10-10 m.

Lösung:

Analyse:

m = 1 kg, d = 10-10 m, mu = 1.66·10-27 kg, Ar(Fe) = 55.847

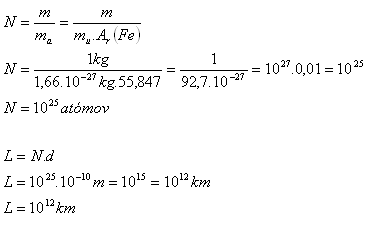
physics-substance-characteristics-3.gif 

In einem Kilogramm Eisen befinden sich 1025 Atome. Die Länge der von diesen Atomen gebildeten Linie wäre 1012 km. Das ist etwa 6600-mal größer als die Entfernung Erde–Sonne.

4.Bestimmen Sie die Anzahl der in 1 g Kupfer enthaltenen Elektronen. Wie groß ist ihre Gesamtmasse, wenn die Masse eines einzelnen Elektrons 9.1·10-31 kg beträgt?

Lösung:

Analyse:

m = 1 g = 10-3 kg, me = 9.1·10-31 kg, mu = 1.66·10-27 kg, Ar(29Cu) = 63.546

Ruhemasse eines Cu-Atoms:

ma(Cu) = mu·Ar(Cu)

ma(Cu) = 1.66·10-27 kg · 63.546 = 105.486·10-27 kg

Anzahl der Atome:

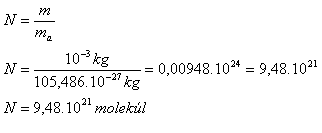
physics-substance-characteristics-4.gif

Anzahl der Elektronen:

29Cu – jedes Atom hat 29 Elektronen

N‘ = 29·N = 29·9.48·1021 = 2.75·1023

Gesamtmasse aller Elektronen:

m = N‘·me = 2.75·1023 · 9.1·10-31 kg = 25·10-8 kg

In einem Gramm Kupfer gibt es 2.75·1023 Elektronen, die eine Masse von 25·10-8 kg haben.

5.Finden Sie heraus, ob ein Molekül Salpetersäure HNO3 eine größere Masse hat als ein Molekül Silberoxid Ag2O. Verwenden Sie Tabellen.

Lösung:

HNO3 

Ar(H) = 1.008

Ar(N) = 14.010

3·Ar(O) = 48.000

Ar(HNO3) = 63.018  m(HNO3) = 63.018·1.66·10-27 kg

                          m(HNO3) = 1.46·10-25 kg

Ag2O 

2·Ar(Ag) = 215.74

Ar(O) = 16.00

Ar(Ag2O) = 231.74     m(Ag2O) = 231.74·1.66·10-27 kg

                          m(Ag2O) = 3.8469·10-25 kg

m(Ag2O) > m(HNO3)

Die Annahme ist nicht korrekt.

6.Berechnen Sie die Stoffmenge, die 4.82·1024 Wasserstoffatomen entspricht.

Lösung:

Analyse:

N = 4.82·1024 Wasserstoffatome, NA = 6.022·1023 mol-1

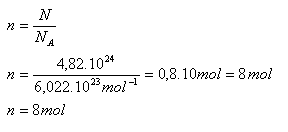
physics-substance-characteristics-6.gif physics-substance-characteristics-6.gif 

Die angegebene Anzahl von Wasserstoffatomen entspricht n = 8 Mol.

7.Bestimmen Sie die Stoffmenge von Wasser mit dem Volumen 3.6 L.

Lösung:

Analyse:

V = 3.6 L, m = 3.6 kg,

2·Ar(H) = 2.016

Ar(O) = 16.000

Ar(H2O) = 18.016

Mm = 18.016·10-3 kg·mol-1

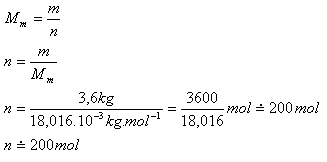
physics-substance-characteristics-7.gif 

Das Volumen 3.6 Liter Wasser entspricht 200 Mol.

8.Prüfen Sie, ob Wasser mit der Stoffmenge 1 mol in einen Zylinder mit dem Volumen 10 cm3 eingefüllt werden kann.

Lösung:

Analyse:

n = 1 mol, V = 10 cm3, Mm = 18.016·10-3 kg (siehe Beispiel 7), ρ = 103 kg·m-3

Volumen eines Mols Wasser:

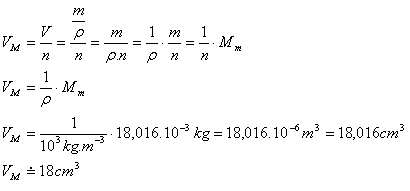
physics-substance-characteristics-8.gif 

Volumen des Zylinders VV = 10 cm3

VM > VV

Das Wasser kann nicht in den Zylinder gegossen werden, weil das Volumen eines Mols Wasser 18 cm3 beträgt und der Behälter nur 10 cm3 fasst.

9.Ein Raum hat die Abmessungen a = 4 m, b = 4 m, c = 3 m. Wie viele Moleküle Luft befinden sich darin? (Mm = 29·10-3 kg·mol-1, ρ = 1.276 kg·m-3)

Lösung:

Analyse:

V = a·b·c

V = 4 m · 4 m · 3 m = 48 m3,

Mm = 29·10-3 kg·mol-1, ρ = 1.276 kg·m-3

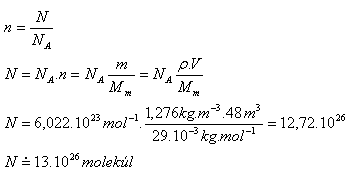
physics-substance-characteristics-9.gif 

Im Raum befinden sich ungefähr 1.3·1027 Moleküle.

10.Von der Oberfläche eines Wassertropfens mit dem Volumen 1 mm3 verdampft in 1 Sekunde Wasser, das etwa 106 Moleküle enthält. In welcher Zeit verdampft der gesamte Tropfen?

Lösung:

Analyse:

V = 1 mm3 = 10-9 m3, N‘ = 1016 s-1, Mm(H2O) = 18.016·10-3 kg·mol-1

ρ = 1000 kg·m-3, NA = 6.022·1023 mol-1

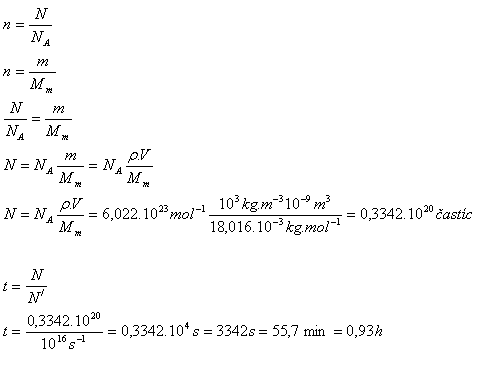
physics-substance-characteristics-10.gif 

Der gesamte Tropfen verdampft in etwas weniger als 1 Stunde.