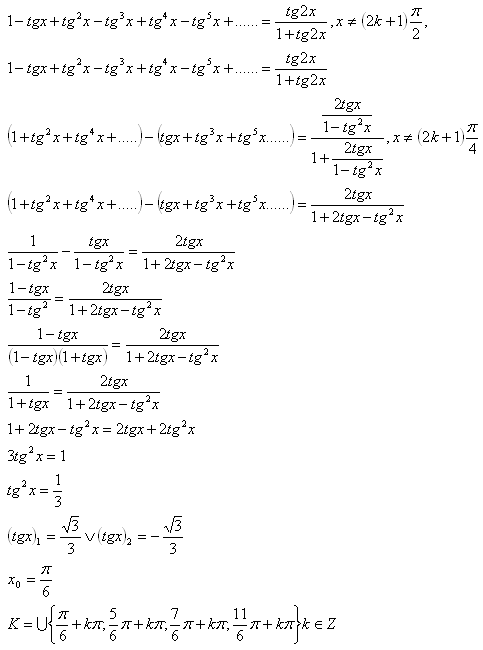Geometrische Folge
1.Charakterisieren Sie die Eigenschaften einer geometrischen Folge:
2.Berechnen Sie die ersten sechs Glieder der geometrischen Folge, wenn gilt a3 = 8 und a7 = 128.
Lösung:
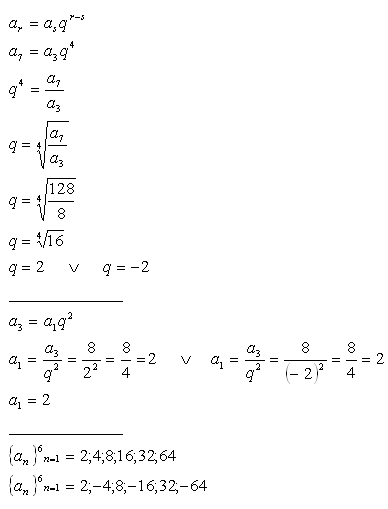
3.Wenn man zu den Zahlen 2, 16 und 58 dieselbe Zahl addiert, erhält man die ersten drei Glieder einer geometrischen Folge. Bestimmen Sie diese Zahl und schreiben Sie die ersten sechs Glieder dieser Folge auf.
Lösung:
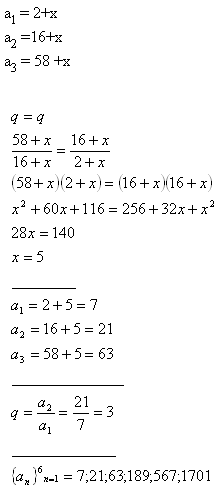
4.Fügen Sie zwischen die Wurzeln der Gleichung x2 -66x +128 = 0 vier Zahlen ein, sodass sie zusammen mit den Wurzeln der Gleichung eine geometrische Folge bilden.
Lösung:
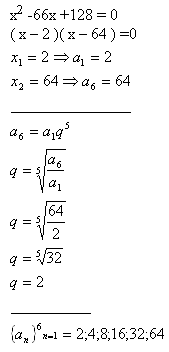
5.Schreiben Sie die ersten sechs Glieder der geometrischen Folge, für die gilt:
Lösung:
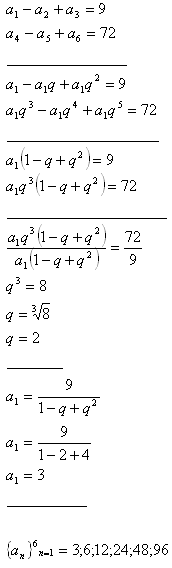
6.Ein Quader, dessen Kanten eine geometrische Folge bilden, hat eine Oberfläche S = 78 cm2.
Die Summe der Kanten, die durch einen Eckpunkt verlaufen, beträgt 13 cm. Bestimmen Sie das Volumen des Quaders.
Lösung:
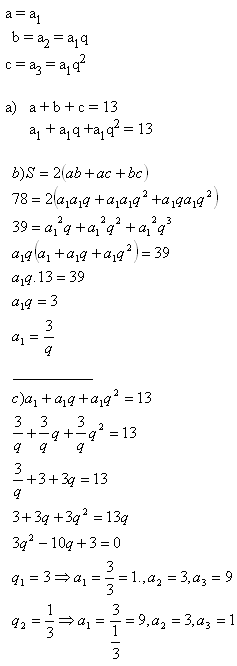
Die Kanten des Quaders sind a = 1 cm, b = 3 cm, c = 9 cm.
Das Volumen des Quaders ist V = a·b·c
V = 1·3·9 cm
3
V = 27 cm
3
7.Ein Reiter beschloss, ein Pferd zu kaufen und dafür 10 000 Sk zu zahlen. Mit dem Verkäufer vereinbarte er, dass er für den ersten Nagel im Hufeisen 1 Heller zahlt, für den zweiten 2 Heller, für den dritten 4 Heller usw.
War es ein vorteilhafter Kauf, wenn jedes Hufeisen mit fünf Nägeln befestigt ist?
Lösung:
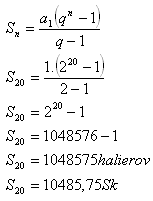
Der Reiter überbezahlte das Pferd um 485,75 Sk / 16,12 €.
*Für die Umrechnung wurde der Konversionskurs 1 EUR = 30,1260 SKK verwendet
8.Ein Aushilfsarbeiter stimmte zu, zu arbeiten, wenn sein Lohn am ersten Tag 1 Sk, am zweiten Tag 2 Sk, am dritten Tag 4 Sk usw. beträgt. Wie viele Tage arbeitete er so, wenn er 4095 Sk verdiente?
Lösung:
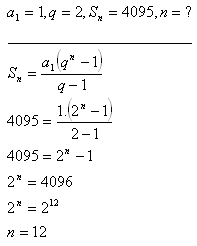
Der Aushilfsarbeiter arbeitete 12 Tage.
9.Zu wie viel % Zinsen muss man eine Summe von 10 000 € anlegen, um nach fünf Jahren 25 000 € auf dem Konto zu haben?
Lösung:
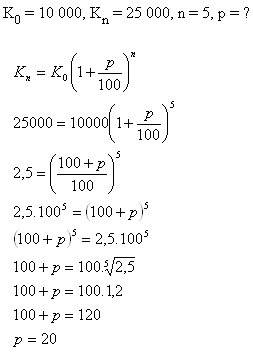
Die Summe muss zu 20 % Zinsen angelegt werden.
10.Berechnen Sie die Summe der unendlichen geometrischen Reihe:
Lösung:
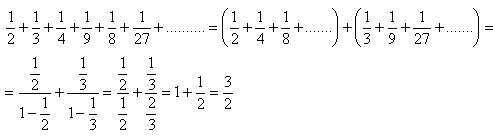
Die Summe der Reihe ist 3/2.
11.Lösen Sie in ℝ die Gleichung:
Lösung:
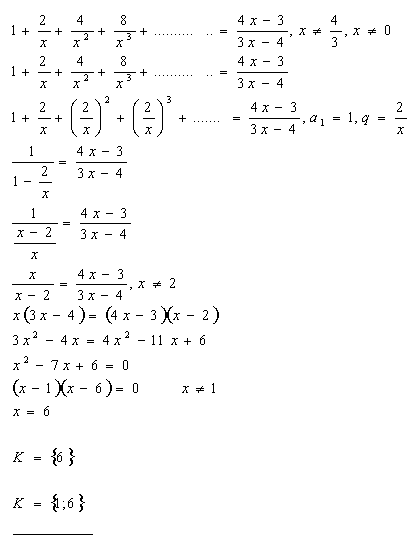
12.Lösen Sie in ℝ die Gleichung:
Lösung: