Wellen

1. Was ist eine mechanische Welle?

Lösung:

Mechanische Wellenbewegung ist ein physikalisches Phänomen, bei dem sich eine mechanische Schwingung in einem elastischen Medium ausbreitet. Bei der Wellenbewegung werden Schwingung und Energie durch das Medium übertragen.
Wellenbewegung kann sein:

a.) Transversalwelle – die Momentanverschiebungen sind senkrecht zur Ausbreitungsrichtung der Welle

gekennzeichnet durch Auf- und Abbewegung

b.) Longitudinalwelle – die Momentanverschiebungen liegen in Ausbreitungsrichtung

gekennzeichnet durch Verdichtung und Verdünnung des Mediums

Phasengeschwindigkeit $v$ – Geschwindigkeit, mit der sich die Welle im Medium ausbreitet

Wellenlänge $λ$

Strecke, die die Welle in der Zeit $T$ zurücklegt
Abstand zweier benachbarter Punkte, die in derselben Phase schwingen
Abstand zweier benachbarter Maxima (oder Minima)
Abstand zweier benachbarter Verdichtungen (oder Verdünnungen)

\lambda = v \cdot T = \frac{v}{f}

Gleichung einer laufenden Welle:

y = y_m \sin \left[ 2\pi \left(\frac{t}{T} - \frac{x}{\lambda}\right) \right]

Die Gleichung einer laufenden Welle beschreibt die Momentanverschiebung der Welle zu einer beliebigen Zeit $t$ und an der Position $x$ .

Interferenz von Wellen – die Überlagerung von zwei oder mehr Wellen

Phasendifferenz:

\Delta \varphi = \frac{2 \pi}{\lambda} (x_2 - x_1) = \frac{2 \pi}{\lambda} d = \frac{\omega}{v} \cdot d

Interferenzmaximum:

d = 2k \cdot \frac{\lambda}{2}, \quad (k = 0, 1, 2, 3, \dots)

Interferenzminimum:

d = (2k + 1) \cdot \frac{\lambda}{2}, \quad (k = 0, 1, 2, 3, \dots)

2.Der Frequenzbereich der menschlichen Sprache liegt zwischen 200 Hz und 1,5 kHz. Bestimmen Sie die kleinste und größte Wellenlänge der entsprechenden Schallwelle! Die Schallgeschwindigkeit in Luft beträgt etwa 340 m.s^-1.

Lösung:

Analyse:

f₁ = 200 s^-1, f₂ = 1500 s^-1, v = 340 m.s^-1.

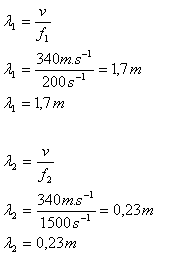
Der Wellenlängenbereich der menschlichen Sprache liegt zwischen 0,23 m und 1,7 m.

3.Von einer Schallquelle breitet sich im Wasser eine Welle mit der Periode T = 2 ms und der Wellenlänge λ = 2,9 m aus. Wie groß ist die Schallgeschwindigkeit im Wasser?

Lösung:

Analyse:

T = 2 ms = 0,002 s, λ = 2,9 m, v = ?

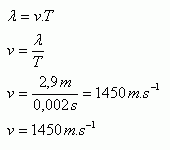
Die Schallgeschwindigkeit im Wasser beträgt v = 1450 m.s^-1.

4.Eine fortschreitende Welle breitet sich in einer elastischen Saite nach der Gleichung aus:

Lösung:

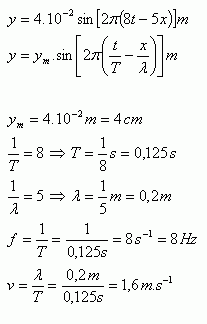
Die fortschreitende Welle ist charakterisiert durch y_m = 4 cm, T = 0,125 s, λ = 0,2 m, f = 8 Hz, v = 1,6 m.s^-1

5.Eine Welle mit der Periode T breitet sich entlang der x-Achse aus. Bei der Koordinate x = 4 cm beträgt zur Zeit t = T/6 die Momentanverschiebung y = 0,5y_m. Bestimmen Sie die Wellenlänge λ!

Lösung:

Analyse:

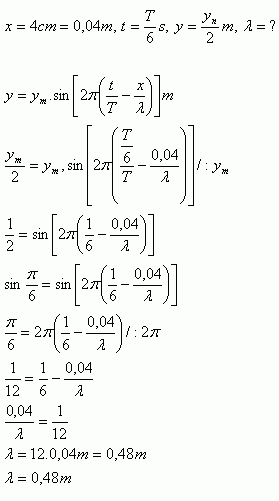
Die Welle hat die Wellenlänge λ = 0,48 m.

6.Eine Welle mit der Periode T und der Wellenlänge λ breitet sich von einer Quelle entlang einer Geraden aus. Zur Zeit t = T/2 hat ein Punkt im Abstand x = λ/3 von der Quelle die Momentanverschiebung y = 5 cm. Bestimmen Sie die Amplitude y_m!

Lösung:

Analyse:

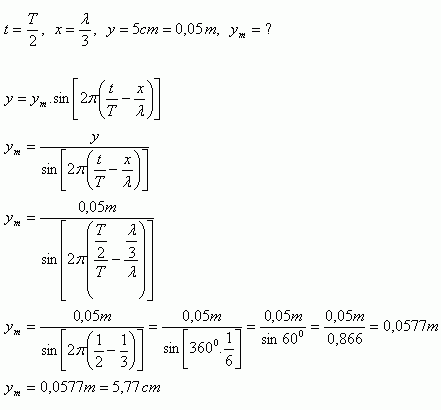
Die Amplitude der Welle beträgt y_m = 5,77 cm.

7.Eine Welle mit der Frequenz 440 Hz breitet sich mit der Phasengeschwindigkeit 340 m.s^-1 aus. Berechnen Sie die Phasendifferenz der Schwingungen zwischen zwei Punkten x₁ und x₂, die auf einer Linie durch die Quelle liegen und einen gegenseitigen Abstand von 17 cm haben.

Lösung:

Analyse:

f = 440 s^-1, v = 340 m.s^-1, d = 17 cm = 0,17 m

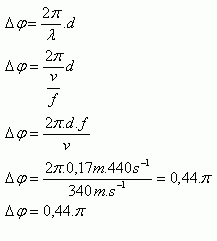
Die Phasendifferenz beträgt Δφ = 0,44π.

8.Entlang einer Geraden breitet sich von einer Quelle eine Welle mit der Periodendauer T = 10^-3s aus. Zwei Punkte dieser Geraden, die sich in den Abständen x₁ = 12 m und x₂ = 14,7 m von der Quelle befinden, schwingen mit der Phasendifferenz 1,5π. Bestimmen Sie die Phasengeschwindigkeit der Welle!

Lösung:

Analyse:

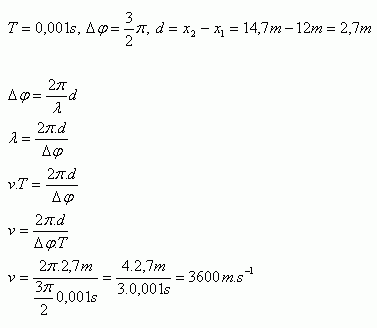
Die Phasengeschwindigkeit der Welle beträgt v = 3600 m.s^-1

Physik

Wellen

Adblock detected