Schwingung
1. Lassen Sie uns einige grundlegende Konzepte der mechanischen Schwingung überprüfen.
Lösung:
Eine Schwingung ist eine Bewegung, bei der ein Körper nach einer Auslenkung mehrmals durch seine Gleichgewichtslage geht. In dieser Lage besitzt der schwingende Körper die geringste potenzielle Energie. Eine Schwingung wird durch folgende Größen charakterisiert:


2.Bestimmen Sie die Periode und Frequenz
- a.) der Nadel einer Nähmaschine, die 20 Stiche pro Sekunde macht
- b.) des Herzschlags, der 75 Schläge pro Minute ausführt
Lösung:
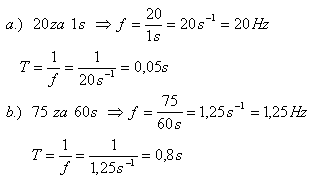
- Nadel: f = 20 Hz, T = 0,05 s.
- Herz: f = 1,25 Hz, T = 0,8 s.
3. Die harmonische Schwingung eines Oszillators wird durch die Gleichung y = 8·sin(4πt + 0,25π) cm beschrieben. Bestimmen Sie:
- a.) die Amplitude der Auslenkung
- b.) die Periode
- c.) die Frequenz
Berechnen Sie die momentane Auslenkung zur Zeit t = 0 s
Lösung:
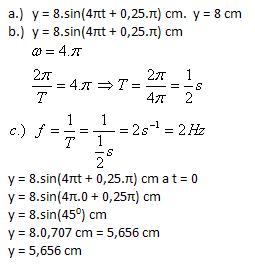
Die momentane Auslenkung zur Zeit t = 0 s beträgt y = 5,656 cm.
4.Die Schwingung eines Oszillators wird durch die Gleichung y = 4·sin(0,5πt) cm beschrieben. Nach welcher Zeit erreicht die momentane Auslenkung des Oszillators die Hälfte der Amplitude?
Lösung:
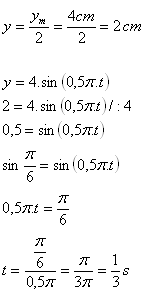
Der Oszillator erreicht die momentane Auslenkung nach t = 1/3 Sekunden.
5. Wie ändert sich die Periode der harmonischen Schwingung, wenn wir anstelle eines Kupferzylinders (ρ1 = 8930 kg·m-3) einen Aluminiumzylinder (ρ2 = 2700 kg·m-3) gleichen Volumens an die Feder hängen?
Lösung:
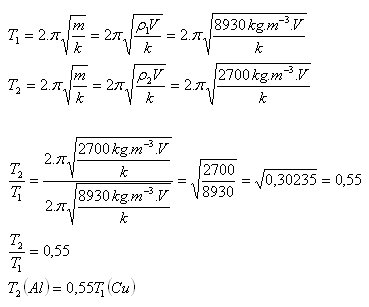
Die Schwingungsperiode verringert sich um etwa das 0,55-Fache.
6. In der Kabine eines Aufzugs hängt ein Pendel mit einer Periode T1 = 1 s. Wenn sich die Kabine mit konstanter Beschleunigung bewegt, schwingt das Pendel mit einer Periode T2 = 1,2 s. Bestimmen Sie die Beschleunigung der Kabine.
Lösung:
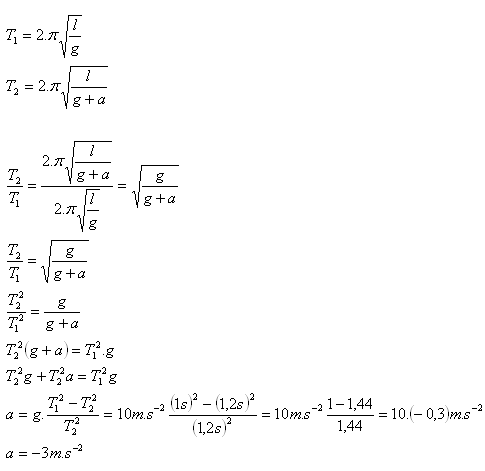
Die Kabine hat eine Beschleunigung von a = –3 m·s-2.
7.Die Eigenperiode der Schwingung eines Eisenbahnwagens beträgt 1,25 s. Durch Stöße an den Schienenstößen erhält der Wagen Kraftimpulse, die ihn in Schwingung versetzen. Bei welcher Zuggeschwindigkeit wird der Wagen am stärksten in Resonanz geraten, wenn die Schienen 25 m lang sind?
Lösung:
Analyse:
T = 1,25 s, s = 25 m, v = ?
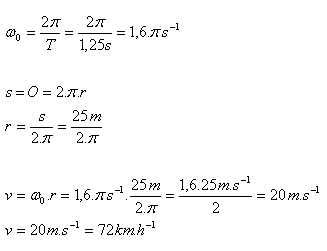
Der Wagen schwingt bei einer Geschwindigkeit von v = 72 km·h-1 am stärksten in Resonanz.
8.Ein materieller Punkt schwingt harmonisch mit der Amplitude ym = 5 cm, der Periode T = 2 s und φ = 0o. Bestimmen Sie die Geschwindigkeit des Punktes in dem Moment, in dem die momentane Auslenkung 2,5 cm beträgt.
Lösung:
Analyse:
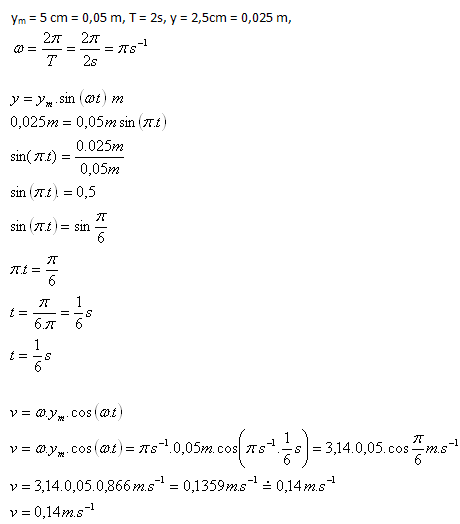
Die Geschwindigkeit des Punktes beträgt v = 0,14 m·s-1.
9.Ein materieller Punkt führt eine harmonische Bewegung aus, die durch die Gleichung y = 5·sin(6πt) cm beschrieben wird. Zu welchem Zeitpunkt ist seine kinetische Energie dreimal so groß wie seine potenzielle Energie?
Lösung:
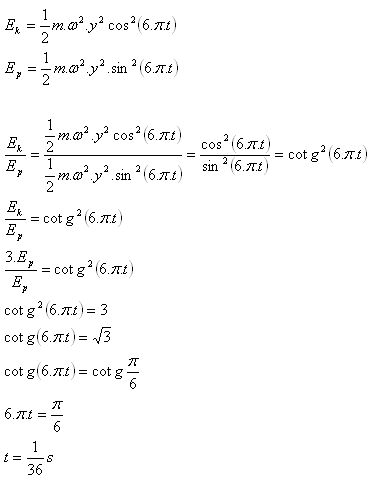
Das geforderte Energieverhältnis tritt zur Zeit t = 1/36 s auf.
10. Die Gesamtenergie eines harmonischen Oszillators beträgt 3·10-5 J und die maximale auf ihn wirkende Kraft ist 1,5·10-3 N. Schreiben Sie die Gleichung der momentanen Auslenkung, wenn der Oszillator eine Periode T = 2 s und eine Anfangsphase φ = 60o hat.
Lösung:
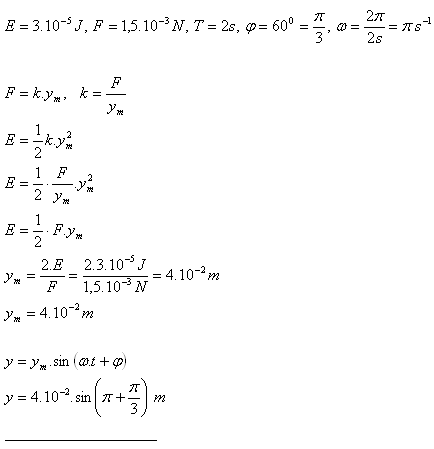
11.Was ist der schnellste Weg, von Europa nach Australien zu gelangen?
Lösung:
Graben Sie einen Tunnel von Europa nach Australien durch das Erdzentrum! Wenn Sie in Europa in den Schacht fallen, werden Sie zwischen Europa und Australien hin- und herschwingen. Die Reisezeit hin und zurück entspricht der Periode dieser Schwingungsbewegung.
