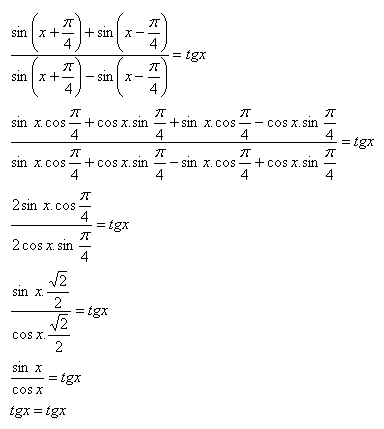Summen- und Differenzformeln
sin (x + y) = sin x · cos y + cos x · sin y
sin (x – y) = sin x · cos y – cos x · sin y
cos (x + y) = cos x · cos y – sin x · sin y
cos (x – y) = cos x · cos y + sin x · sin y
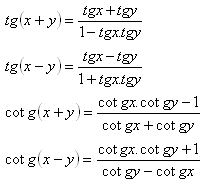
1.Vereinfachen Sie:
Lösung:
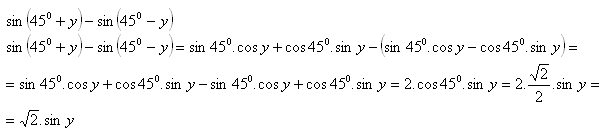
2.Berechnen Sie:
Lösung:
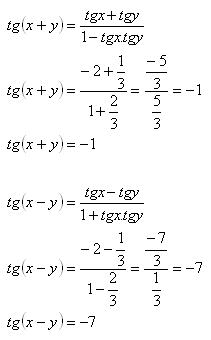
3.Beweisen Sie die Identität:
sin(x + y) + cos(x – y) = (sin x + cos x)(sin y + cos y)
Lösung:
sin(x + y) + cos(x – y) = (sin x + cos x)(sin y + cos y)
sin x · cos y + cos x – sin y + cos x · cos y + sin x · sin y = (sin x + cos x)(sin y + cos y)
sin x · (sin y + cos y) + cos x · (sin y + cos y) = (sin x + cos x)(sin y + cos y)
(sin y + cos y)(sin x + cos x) = (sin x + cos x)(sin y + cos y)
Die Identität gilt.
4.Beweisen Sie die Identität, wenn 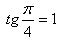 gilt:
gilt:
Lösung:
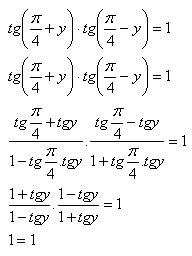
Die Identität gilt, wenn
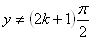
5.Schreiben Sie die Formeln für die Summe und Differenz der goniometrischen Funktionen auf:
Lösung:
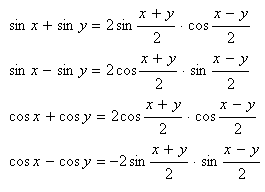
6.Vereinfachen Sie:
Lösung:
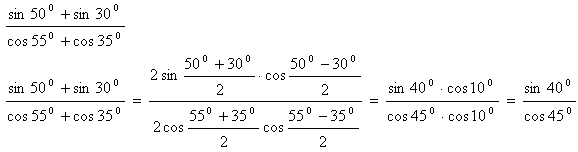
7.Beweisen Sie, dass gilt, wenn gilt: 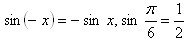
Lösung:
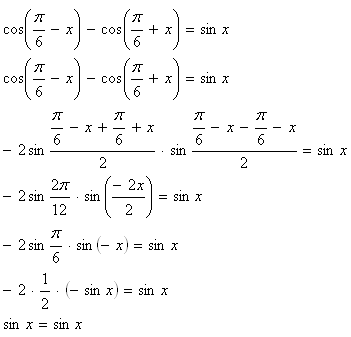
Die Identität gilt.
8.Beweisen Sie, dass gilt:
Lösung:
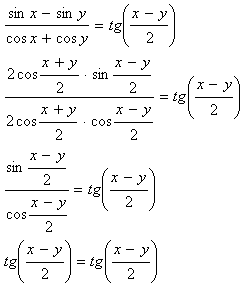
Die Identität gilt, wenn (x – y) ≠ (2k + 1)π
9.Zeigen Sie, dass die Identität gilt:
Lösung:
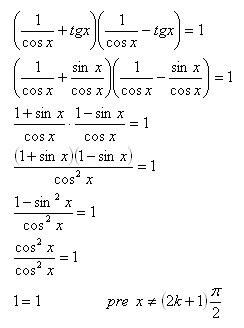
10.Zeigen Sie, dass die Identität gilt:
Lösung: