sk|cz|en|

Physik

Akustik

1.Was ist Akustik?

Lösung:

Akustik ist der Zweig der Physik, der sich mit den physikalischen Phänomenen bei der Ausbreitung von Schall befasst. Eine Schallquelle ist jeder Körper, der schwingen kann.

Schall:
a) Ton – eine regelmäßige sinusförmige Welle (menschliche Stimmbänder, Saiten, Luftsäulen, Musikinstrumente)
b) Geräusch – eine unregelmäßige Wellenform (Knallen, Rauschen, Knarren)

Schallintensität:

I=PS=Wt⋅S,[I]=W m−2I=\frac{P}{S}=\frac{W}{t\cdot S},\qquad [I]=\mathrm{W\,m^{-2}}

Hörschwelle I0=10−12 W m−2, Schmerzschwelle Ib=10 W m−2

Schallintensitätspegel:

L=10⋅log⁡ ⁣(II0),[L]=dB (Dezibel)L = 10 \cdot \log\!\left(\frac{I}{I_0}\right),\qquad [L]=\mathrm{dB}\ \text{(decibel)}

Tonhöhe – bestimmt durch die Frequenz der Schwingung

fz=v2lf_z=\frac{v}{2l}

Klangfarbe – bestimmt durch das Vorhandensein höherer Oberwellen

fk=k⋅v2lf_k = k\cdot \frac{v}{2l}

Schallgeschwindigkeit in Luft:

v=(331.8+0.61 t) m s−1v = (331.8 + 0.61\,t)\ \mathrm{m\,s^{-1}}

(wobei t tdie Temperatur in °C ist)

Saite:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Offenes Rohr:

l=kλ2  (k=1,2,3,…),fz=v2ll = k\frac{\lambda}{2}\ \ (k=1,2,3,\ldots), \qquad f_z=\frac{v}{2l}

Geschlossenes Rohr:

l=kλ4  (k=1,3,5,…),fz=v4ll = k\frac{\lambda}{4}\ \ (k=1,3,5,\ldots), \qquad f_z=\frac{v}{4l

  

2.Berechne die Schallgeschwindigkeit in Luft

  • a.) bei der Temperatur t = 0o C
  • b.) bei der Temperatur t = 15o C
  • c.) bei welcher Temperatur beträgt die Schallgeschwindigkeit in Luft v = 351.32 m·s-1? Die Schallgeschwindigkeit in Luft in Abhängigkeit von der Umgebungstemperatur ist gegeben durch v = 331.8 + 0.61·t  (m·s-1).

Lösung:

a.) t = 0oC, v0 = (331,8 + 0,61·0) m·s-1 = 331,8 m·s-1 => v0 = 331,8 m·s-1

b.) t = 15oC, v15 = (331,8 + 0,61·15oC) m·s-1 = 340 m·s-1 => v15 = 340 m·s-1

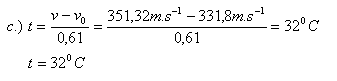
fyzika-akustika-2.gif 

Die Schallgeschwindigkeiten in Luft sind v0 = 331,8 m·s-1, v15 = 340 m·s-1.

Die Schallgeschwindigkeit in Luft v = 351,32 m·s-1 wird bei der Temperatur t = 32oC erreicht.

Die Schallgeschwindigkeit v15 = 340 m·s-1 wird beim Lösen von Aufgaben verwendet (sofern nicht anders angegeben).

3.Berechne die Wellenlängen, die den Grenzen des hörbaren Frequenzbereichs 16 Hz – 20 000 Hz entsprechen. v = 340 m·s-1.

Lösung:

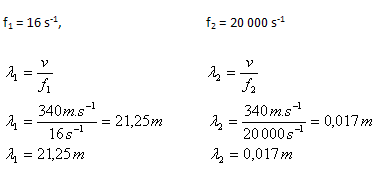
fyzika-akustika-3.gif 

Die den Hörbarkeitsgrenzen entsprechenden Wellenlängen sind 0.017 m – 21.25 m.

4.Vier Aufgaben zum Meer …

  • a.) Auf der Meeresoberfläche befinden sich zwei Boote in einem gegenseitigen Abstand von 11,6 km. Das erste sendet durch das Wasser ein Schallsignal und gleichzeitig darüber ein Lichtsignal. Das zweite Boot empfängt beide Signale, das Schallsignal 8 s später als das Licht. Bestimme die Schallgeschwindigkeit im Meerwasser.
  • b.) Ein Matrose auf einem Boot hörte den Donner 10 s, nachdem er den Blitz gesehen hatte. In welcher Entfernung schlug der Blitz ein?
  • c.) Vom Echo einer Walgruppe reflektierter Schall kehrte nach 1 Sekunde zum Boot zurück. Wie weit sind die Wale vom Boot entfernt?
  • d.) Auf einem Boot wurde die Meerestiefe mit Ultraschall gemessen. Wie groß ist die Tiefe dort, wenn das reflektierte Ultraschallsignal nach 0,8 s zum Boot zurückkehrte?

Lösung:

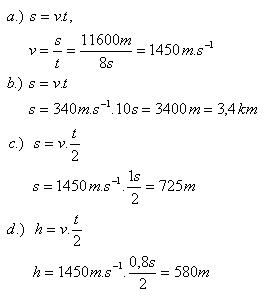
fyzika-akustika-4.gif

5.Ein Beobachter am Rand der Macocha-Schlucht ließ einen Stein hinabfallen und hörte den Aufprall nach 5,6 s. Bestimme die Tiefe der Schlucht!

t1 – Fallzeit des Steins,  t2 – Laufzeit des Schalls nach dem Aufprall am Boden

Lösung:

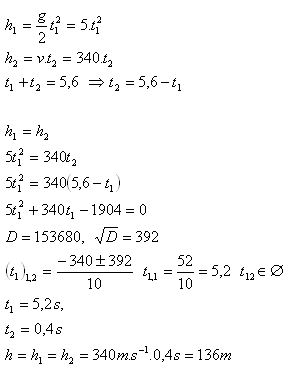
fyzika-akustika-5.gif 

Die Tiefe der Macocha-Schlucht beträgt etwa 136 m.

6.Wenn wir die Länge einer Saite (bei unveränderter Spannung) um 10 cm verkürzen, ändert sich ihre Grundfrequenz um den Faktor 1,5. Bestimme die ursprüngliche Länge der Saite l.

Lösung:

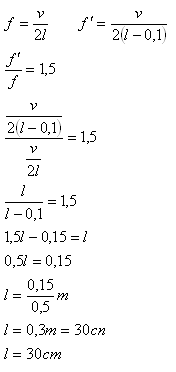
fyzika-akustika-6.gif 

Die ursprüngliche Länge der Saite war l = 30 cm.

7. Welche Länge muss

  • a.) ein offenes Rohr haben
  • b.) ein geschlossenes Rohr haben
wenn sie bei der Temperatur t = –5oC einen Ton mit der Frequenz f = 130.5 Hz erzeugen?

Lösung:

Analyse:

v = 331,8 + 0,61·t

v–5 = (331,8 + 0,61·(–5)) m·s-1 = 328,75 m·s-1 

a.) Offenes Rohr:

f=v2lf = \frac{v}{2l}l=v2f=328.75 m⋅s−12⋅130.5 s−1=1.26 ml = \frac{v}{2f} = \frac{328.75\ \mathrm{m·s^{-1}}}{2 \cdot 130.5\ \mathrm{s^{-1}}} = 1.26\ \mathrm{m}

b.) Geschlossenes Rohr:

f=v4lf = \frac{v}{4l}l=v4f=328.75 m⋅s−14⋅130.5 s−1=0.63 ml = \frac{v}{4f} = \frac{328.75\ \mathrm{m·s^{-1}}}{4 \cdot 130.5\ \mathrm{s^{-1}}} = 0.63\ \mathrm{m}

 

 Das offene Rohr muss 1.26 m lang sein, das geschlossene 0.63 m.

8.Um wie viele Dezibel steigt der Schallintensitätspegel, wenn die Schallintensität sich um das 100 000-Fache erhöht? Wie groß ist diese erhöhte Intensität?

Lösung:

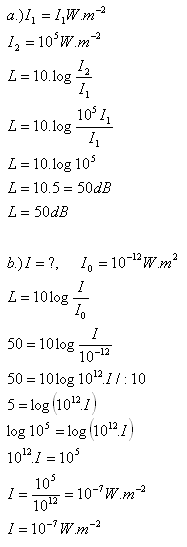
fyzika-akustika-8.gif 

Der Schallintensitätspegel steigt um 50 dB.

Die erhöhte Schallintensität beträgt I = 10-7 W·m-2.

9.Was ist das Doppler-Prinzip (Doppler-Effekt)?

Lösung:

Das Doppler-Prinzip erklärt die Änderung der beobachteten Frequenz von Schallwellen, die durch die Relativbewegung von Schallquelle und Beobachter verursacht wird.

Sei v – Schallgeschwindigkeit, u – Geschwindigkeit des Beobachters,

w – Geschwindigkeit der Schallquelle, f – von der Quelle emittierte Frequenz,

f‘ – vom Beobachter wahrgenommene Frequenz.

A.) Beobachter und Quelle bewegen sich aufeinander zu:

f′=fv+uv−wf' = f \frac{v + u}{v - w}

B.) Beobachter und Quelle entfernen sich voneinander:

f′=fv−uv+wf' = f \frac{v - u}{v + w

Hinweis: Johann Christian Doppler (1803 – 1853), österreichischer Mathematiker und Physiker. Er arbeitete in Wien, Prag und an der Bergakademie in Banská Štiavnica (1847).

10.
John steht an einer Autobahn, auf der ein Krankenwagen mit der Geschwindigkeit w = 20 m·s-1 fährt. Die Sirene des Krankenwagens sendet einen konstanten Ton mit der Frequenz 1 000 Hz aus. Welche Frequenz registriert John, wenn der Krankenwagen

  • a.) sich nähert
  • b.) sich entfernt. 
Die Lufttemperatur ist t = 20oC

Lösung:

Analyse:

v = 331,8 + 0,61·20 = 344 m·s-1, w = 20 m·s-1, f = 1 000 Hz, u = 0

a.) Der Krankenwagen nähert sich:

f′=fv+uv−w,und da u=0f' = f \frac{v + u}{v - w}, \quad \text{and since } u = 0f′=fvv−wf' = f \frac{v}{v - w}f′=1000 s−1344 ms−1(344−20) ms−1=1000 s−1×1.062=1062 s−1f' = 1000\,\text{s}^{-1} \frac{344\,\text{m·s}^{-1}}{(344 - 20)\,\text{m·s}^{-1}} = 1000\,\text{s}^{-1} \times 1.062 = 1062\,\text{s}^{-1} f′=1062 Hzf' = 1062\,\text{Hz}

b.) Der Krankenwagen entfernt sich:

f′=fvv+w,und da u=0f' = f \frac{v - u}{v + w}, \quad \text{and since } u = 0f′=fvv+wf' = f \frac{v}{v + w}f′=1000 s−1344 ms−1(344+20) ms−1=1000 s−1×0.945=945 s−1f' = 1000\,\text{s}^{-1} \frac{344\,\text{m·s}^{-1}}{(344 + 20)\,\text{m·s}^{-1}} = 1000\,\text{s}^{-1} \times 0.945 = 945\,\text{s}^{-1}f′=945 Hzf' = 945\,\text{Hz}

 


John registriert im ersten Fall eine Frequenz von 1062 Hz und im zweiten Fall 945 Hz.