sk|cz|en|

Physik

Innere Energie

1. Was ist die innere Energie eines Systems und wie kann sie verändert werden?

Lösung:

Ein thermodynamisches System ist eine Menge mikroskopischer und makroskopischer Objekte, die ein Ganzes bilden und Energie untereinander oder mit der Umgebung austauschen können. Die Gesamtenergie des Systems ist die Summe aus der gesamten kinetischen Energie der ungeordneten Bewegung der Teilchen und der gesamten potenziellen Energie der gegenseitigen Lage dieser Teilchen.

U = Ek + EP

Erster Hauptsatz der Thermodynamik:

Die Änderung der inneren Energie des Systems ΔU ist gleich der Summe aus der Arbeit W, die von äußeren, mit Kräften einwirkenden Körpern am System verrichtet wird, und der Wärme Q, die dem System von der Umgebung zugeführt wird.

ΔU = W + Q

  • a.) Das System nimmt Energie auf (Arbeit, Wärme): W > 0, Q > 0
  • b.) Das System gibt Energie ab (Arbeit, Wärme): W < 0, Q < 0

Änderung der inneren Energie durch äußere Arbeit: (Q = 0)

ΔU=Ep=m⋅g⋅h\Delta U = E_p = m \cdot g \cdot h ΔU=Ek=12mv2\Delta U = E_k = \frac{1}{2} m v^2

Änderung der inneren Energie durch Wärmeaustausch: (W = 0)

Wärmekapazität:

C=QΔt[C]=J⋅K−1C = \frac{Q}{\Delta t} \quad [C] = J \cdot K^{-1}

Spezifische Wärmekapazität (Tabellen):

c=Cm=Qm⋅Δt[c]=J⋅kg−1⋅K−1c = \frac{C}{m} = \frac{Q}{m \cdot \Delta t} \quad [c] = J \cdot kg^{-1} \cdot K^{-1}

Wärmemenge, die ein System aufnimmt (oder abgibt):

Q=m⋅c⋅(t2−t1)[Q]=JQ = m \cdot c \cdot (t_2 - t_1) \quad [Q] = J

Kalorimetrische Gleichung (Mischungsregel):

m1c1(t−t1)=m2c2(t2−t)t1<t<t2m_1 c_1 (t - t_1) = m_2 c_2 (t_2 - t) \quad t_1 < t < t_2

Mit Kalorimeter:

m1c1(t−t1)+C(t−t1)=m2c2(t2−t)m_1 c_1 (t - t_1) + C (t - t_1) = m_2 c_2 (t_2 - t)


 

2.Der englische Physiker J. P. Joule (1818 – 1889) versuchte, die spezifische Wärmekapazität von Wasser zu bestimmen. In seinem Experiment verwendete er zwei Gewichte mit je 14 kg Masse und ließ sie 12-mal hintereinander aus einer Höhe von 2 m in einen Behälter mit Wasser fallen. Der Behälter enthielt Wasser mit der Masse 6.7 kg. Während des Experiments stieg die Temperatur des Wassers um 0.24 K. Welchen Wert der spezifischen Wärmekapazität des Wassers ermittelte er?

Lösung:

Analyse:

2.m1 = 28 kg, Ep = 2.m1.g.h = 28kg.10m.s-2.2m = 560 J,

Ek = 12.Ep = 12.560J = 6720 J, m2 = 6,7kg, Δt = 0,24 K

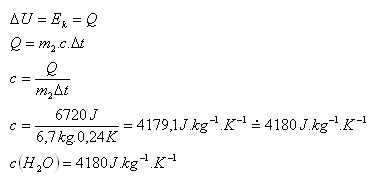
fyzika-vnutorna-energia-2.gif 

Spezifische Wärmekapazität von Wasser c(H2O) = 4180 J·kg-1·K-1

3.Denk über einen kurzen Test nach: Wenn T(K) = t(°C) + 273.15, welche Aussage ist dann richtig?

Temperatur 0oC ist

A) –100oK B) 0oK C) 273.15 K

 

2) Temperatur -273.15 ist

A) der Gefrierpunkt von Helium B) absoluter Nullpunkt C) Unsinn

 

3) Temperatur 185.2 oC ist

A) –85.2 K B) 458.35 K C) 358.35 K

 

4) Temperatur 0 K ist

A) Unsinn B) –273.15oC C) 273.150oC

 

5) Ein Schüler sagte: „Die Temperatur des Wassers stieg um 20oK.“ In Wirklichkeit stieg sie um

A) 20oC B) 293.15oC C) 253.15oC

 

6) Temperatur –1273.15oC ist

A) der Gefrierpunkt von Wasserstoff B) Unsinn C) 73.15 K

 

7) Temperatur 290 K ist

A) die Temperatur eines gesunden Menschen B) 290oC C) 16.85oC

 

8) Temperatur 373.15 K ist

A) Siedetemperatur von Wasser B) Unsinn C ) 0oC

Lösung:

1C, 2B, 3B, 4B, 5A, 6B, 7C, 8A

4.Ein Stahlstab hat die Wärmekapazität C = 1.5·103 J·K-1. Wie ändert sich seine Temperatur, wenn

  • a) er Wärme Q1= 25·103 J aufnimmt
  • b) er Wärme Q2 = 0.45·106 J abgibt

Lösung:

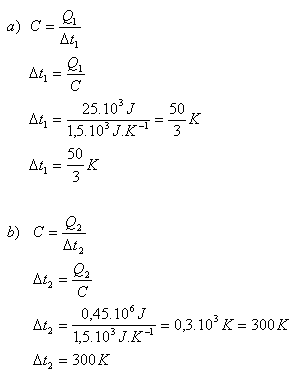
fyzika-vnutorna-energia-4.gif 

  • a) die Temperatur steigt um 50/3 K
  • b) die Temperatur sinkt um 300 K.

5.Berechne, wie lange es dauert, bis Wasser von 15oC bis zur Siedetemperatur erhitzt ist, wenn es mit einem Tauchsieder erwärmt wird und das Wasservolumen 150 cm3 beträgt. Die Leistung des Heizers ist 500 W, sein Wirkungsgrad 95%. c(H2O) = 4180 J·kg-1·K-1.

Lösung:

Analyse:

Δt = 100oC – 15oC = 85oC, V = 150·10-6 m3, Pin = 500 W, η = 0.95

c(H2O) = 4180 J·kg-1·K-1, ρ(H2O) = 103 kg·m-3

Vom Wasser aufgenommene Wärmemenge:

Q=m⋅c⋅Δt=ρ⋅V⋅c⋅ΔtQ = m \cdot c \cdot \Delta t = \rho \cdot V \cdot c \cdot \Delta t Q=103 kg.m−3⋅150⋅10−6 m3⋅4180 J.kg−1.K−1⋅85 K=5.3295⋅104 JQ = 10^3 \, \text{kg·m}^{-3} \cdot 150 \cdot 10^{-6} \, \text{m}^3 \cdot 4180 \, \text{J·kg}^{-1}\text{·K}^{-1} \cdot 85 \, K = 5.3295 \cdot 10^4 \, J Q=5.3295⋅104 JQ = 5.3295 \cdot 10^4 \, J

Erwärmungszeit des Wassers:

η=PPpP=η⋅Pp\eta = \frac{P}{P_p} \quad P = \eta \cdot P_p P=QτP = \frac{Q}{\tau} τ=QP=Qη⋅Pp\tau = \frac{Q}{P} = \frac{Q}{\eta \cdot P_p} τ=5.3295⋅104 J0.95⋅500 W=112.2 JJ/s=112.2 s=1.87 min=1 min 52 s\tau = \frac{5.3295 \cdot 10^4 \, J}{0.95 \cdot 500 \, W} = 112.2 \, \frac{J}{J/s} = 112.2 \, s = 1.87 \, min = 1 \, min \, 52 \, s τ=1.87 min=1 min 52 s\tau = 1.87 \, min = 1 \, min \, 52 \, s

Das Wasser erwärmt sich in knapp 2 Minuten.

6.Zu Wasser mit der Masse 2.5 kg und der Temperatur 15oC wurde ein Stahlzylinder mit der Masse 0.9 kg und der Temperatur 300oC gegeben. Wie hoch ist die Endtemperatur von Wasser und Zylinder nach dem Erreichen des Gleichgewichts?

Lösung:

Analyse:

m1 = 2.5 kg,  m2 = 0.9 kg,  t1 = 15oC,  t2 = 300oC
c1(H2O) = 4180 J·kg-1·K-1,  c2(Fe) = 452  J·kg-1·K-1
t = ?

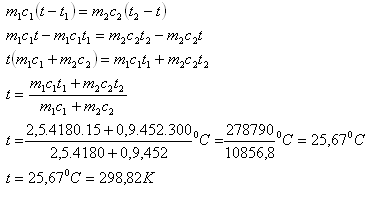
 fyzika-vnutorna-energia-6.gif

Die Endtemperatur von Wasser und Zylinder beträgt t = 25.67oC.

7.Fünf Stahlplatten mit einer Gesamtmasse von 7 kg wurden auf 910oC erhitzt und in Öl bei 10oC eingetaucht. Wie viele Liter Öl müssen wir für das Abschreckbad verwenden, damit sich die Badtemperatur bei 190oC stabilisiert?

Lösung:

Analyse:

Öl: t1 = 10oC, c1 = 1760 J·kg-1·K-1, ρ1 = 940 kg·m-3, m1 = ? V1 = ?

Platten: t2 = 910oC, c2 = 452 J·kg-1·K-1, m2 = 7 kg,

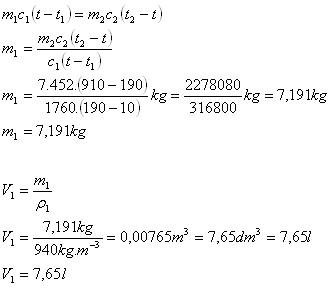
fyzika-vnutorna-energia-7.gif 

Endtemperatur t = 190oC

8.In einem Behälter befinden sich 0.42 kg Wasser bei 20oC. Gießen wir weitere 0.9 kg Wasser mit 70oC in den Behälter, so stellt sich nach dem Erreichen des Gleichgewichts eine Endtemperatur von 50oC ein. Wie groß ist die Wärmekapazität des Behälters?

Lösung:

Analyse:

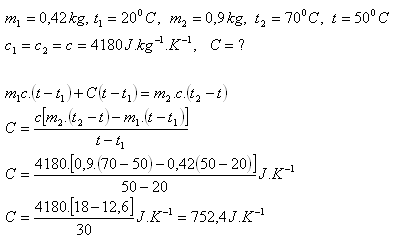
 fyzika-vnutorna-energia-8.gif

Die Wärmekapazität des Behälters beträgt C = 752.4 J·K-1

9.In einen Behälter mit C = 2 J·K-1 wurde Wasser mit der Masse 0.4 kg und der Temperatur 17oC gegossen. Ein Zylinder unbekannten Materials mit der Masse 0.124 kg und der Temperatur 64oC wurde in den Behälter gelegt. Die Systemtemperatur glich sich bei 19oC aus. Aus welchem Material besteht der Zylinder? Verwende Tabellen!

Lösung:

Analyse:

Wasser: m1 = 0.4 kg,  t1 = 17oC,  c1 = 4180 J·kg-1·K-1 Zylinder: m2 = 0.124 kg,  t2 = 64oC,  c2 = ?
Systemtemperatur: t = 19oC
Behälter: C = 2 J·K-1

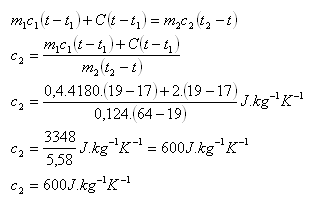
fyzika-vnutorna-energia-9.gif 

Der Zylinder besteht aus Messing. (c(Messing) = 590 J·kg-1·K-1)

10.Beim Mischen von 20 Litern Wasser bei 12oC mit 40 Litern Wasser bei 80oC entweichen 420 kJ Wärme an die Luft. Bestimme die Endtemperatur des Wassers!

Lösung:

Analyse:

m1 = 20 kg,  t1 = 12oC   m2 = 40 kg,  t2 = 80oC, Q = 420·103 J,
c1 = c2 = c = 4180 J·kg-1·K-1,  t = ?

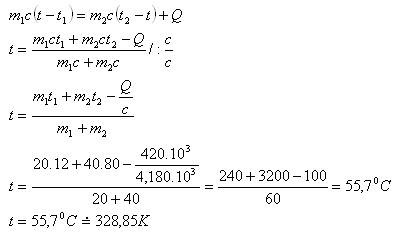
fyzika-vnutorna-energia-10.gif

Die Endtemperatur des Wassers beträgt t = 55.7oC