sk|cz|en|

Physik

Wärmeausdehnung

1. Charakterisieren Sie die Wärmeausdehnung von Festkörpern, Flüssigkeiten und Gasen!

Lösung:

Die Wärmeausdehnung ist eine Änderung der Abmessungen eines Körpers, die durch eine Änderung seiner Temperatur verursacht wird.

A.) Festkörper

1.) Lineare Ausdehnung:

l=l0(1+α⋅Δt)l = l_0 (1 + \alpha \cdot \Delta t)

α\alpha = Koeffizient der linearen Wärmeausdehnung

  • α(Cu)=1.7×10−5 K−1\alpha(\text{Cu}) = 1.7 \times 10^{-5} \, K^{-1}

  • α(Al)=2.4×10−5 K−1\alpha(\text{Al}) = 2.4 \times 10^{-5} \, K^{-1}

  • α(Fe)=1.2×10−5 K−1\alpha(\text{Fe}) = 1.2 \times 10^{-5} \, K^{-1}

Relative Längenzunahme:

ε=Δll0⋅100%\varepsilon = \frac{\Delta l}{l_0} \cdot 100 \%

Volumenausdehnung:

V=V0(1+3α⋅Δt)V = V_0 (1 + 3 \alpha \cdot \Delta t) ρ=ρ0(1−3α⋅Δt)\rho = \rho_0 (1 - 3 \alpha \cdot \Delta t)

Flüssigkeiten

Volumenausdehnung:

V=V0(1+β⋅Δt)V = V_0 (1 + \beta \cdot \Delta t)

β\beta = Koeffizient der thermischen Volumenausdehnung

  • β(H2O)=1.8×10−4 K−1\beta(\text{H}_2\text{O}) = 1.8 \times 10^{-4} \, K^{-1}

  • β(diesel)=1.1×10−3 K−1\beta(\text{diesel}) = 1.1 \times 10^{-3} \, K^{-1}

ρ=ρ0(1−β⋅Δt)\rho = \rho_0 (1 - \beta \cdot \Delta t)

Gase

1.) Volumenausdehnung:

V=V0(1+γ⋅Δt)V = V_0 (1 + \gamma \cdot \Delta t)

γ\gamma = Ausdehnungskoeffizient ist für alle Gase gleich:

γ=1273.16 K=0.00366 K−1=3.66×10−3 K−1\gamma = \frac{1}{273.16 \, K} = 0.00366 \, K^{-1} = 3.66 \times 10^{-3} \, K^{-1}


2.Ein Kupferdraht (α = 1,7·10-5K-1) hatte bei einer Temperatur von -50C eine Länge von 21,55 m. Wie groß ist seine Länge bei 300C? Um wie viele cm hat sich der Draht verlängert?

Lösung:

Analyse:

l0 = 21,55 m,  α = 1,7·10-5K-1 = 0,000017 K-1,  Δt = 300C - (-50C) = 350C

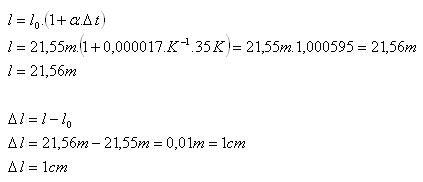
fyzika-tepelna-roztaznost-2.gif 

Nach dem Erwärmen hat der Draht eine Länge von 21,56 m. Er hat sich um 1 cm verlängert.

3.Ein Kupferdraht (α = 1,7·10-5K-1), dessen Länge bei 180C 150 cm betrug, wurde durch elektrischen Strom erhitzt und verlängerte sich um 9 mm. Auf welche Temperatur wurde der Draht erhitzt?

Lösung:

Analyse:

l0 = 150 cm = 1,5 m,   t1 = 180C,  Δl = 0,009 m,   α = 1,7·10-5K-1

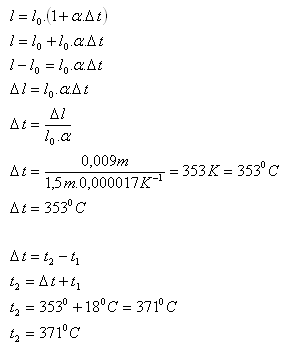
 fyzika-tepelna-roztaznost-3.gif

Der Draht wurde auf eine Temperatur von 3710C erhitzt.

4.Zwei Stäbe, einer aus Eisen (α1 = 1,2·10-5K-1) und einer aus Zink (α2 = 2,9·10-5K-1), hatten bei 00C die gleiche Länge. Bei einer Temperaturerhöhung auf 1000C beträgt der Unterschied ihrer Längen 1 cm. Wie lang waren sie ursprünglich?

Lösung:

Analyse:

α1 = 1,2·10-5K-1,  α2 = 2,9·10-5K-1,  Δt = 100 K,  Δl = 0,01 m

 fyzika-tepelna-roztaznost-4.gif

Die ursprünglichen Längen der Stäbe waren l0 = 5,88 m.

5.Ein Aluminiumbehälter (α (Al) = 24·10-6K-1) hat bei 200C ein Innenvolumen von 10 Litern. Wie ändert sich sein Innenvolumen bei 1000C?

Lösung:

Analyse:

α (Al) = 24·10-6K-1,  t1 = 200C,  t2 = 1000C,  Δt = 800C = 80 K,
V0 = 10 l = 10 dm3 = 10-2 m3

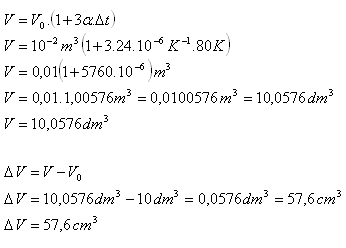
 fyzika-tepelna-roztaznost-5.gif

Das Innenvolumen des Behälters vergrößert sich um 57,6 cm3.

6.Tabellen geben an, dass Kupfer bei 200C eine Dichte von ρ20 = 8930 kg·m-3 hat. Wie groß ist die Dichte von Kupfer bei 800C?

Lösung:

Analyse:

ρ20 = 8930 kg·m-3,  t1 = 200C,  t2 = 800C,  Δt = 600C = 60 K, α(Cu) = 1,7·10-5K-1

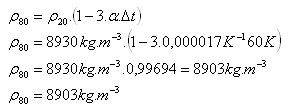
fyzika-tepelna-roztaznost-6.gif 

Die Dichte von Kupfer bei 800C beträgt ρ80 = 8903 kg·m-3.

7.Eine Bodenfliese besteht aus Marmor (α = 0,85·10-5K-1) und ist quadratisch. Die Seitenlänge der Fliese beträgt bei 00C 0,5 m. Um wie viele cm2 vergrößert sich die Fläche der Fliese, wenn ihre Temperatur auf 350C erhöht wird?

Lösung:

Analyse:

α = 0,85·10-5K-1,  a0 = 0,5 m,  Δt = 350C,  ΔS = ?

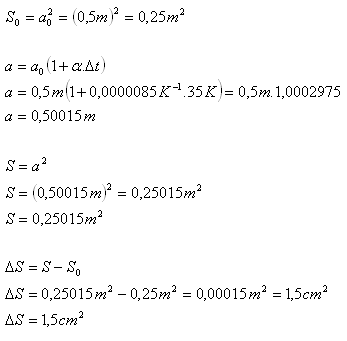
fyzika-tepelna-roztaznost-7.gif 

Die Fläche der Fliese nimmt um 1,5 cm2 zu.

8.Eine Messingkugel (α = 1,8·10-1K-1) hat bei 150C einen Radius r1 = 2 cm. Um wie viele 0C muss sie erhitzt werden, damit sie nicht mehr durch eine runde Öffnung mit dem Radius r2 = 2,02 cm passt?

Lösung:

Analyse:

α = 1,8·10-1K-1,  r1 = 2 cm,  r2 = 2,02 cm,

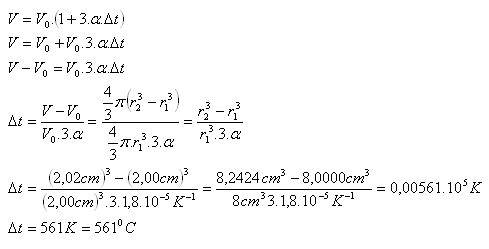
fyzika-tepelna-roztaznost-8.gif 

Die Messingkugel muss um 5610C bis 5760C erhitzt werden.

9.Ein Kesselwagen ist bis zur Öffnung mit Diesel gefüllt. (ρ = 940 kg·m-3, β = 1·10-3K-1) Bei 00C fasst der Wagen 50 Tonnen Diesel. Wie viel Diesel läuft aus der Öffnung aus, wenn die Temperatur des Diesels während der Fahrt auf 200C steigt?

Lösung:

Analyse:

ρ0 = 940 kg·m-3,  β = 1·10-3K-1, m0 = 50 000 kg,  Δt = 200C = 20 K

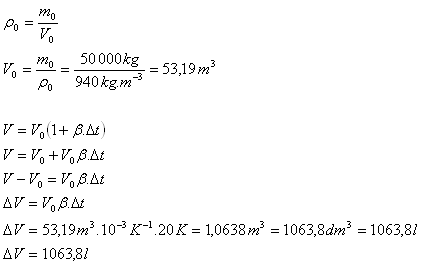
 fyzika-tepelna-roztaznost-9.gif

Es werden 1 063,8 Liter Diesel aus dem Wagen auslaufen.

10.Die Luft in einem Gefäß mit beweglichem Kolben hat bei 100C ein Volumen von 1 Liter. Wie groß ist das Luftvolumen bei 400C? Berechnen Sie außerdem die relative Volumenänderung!

Lösung:

Analyse:

V0 = 1 l = 1 dm3 = 1000 cm3,  Δt = 300C = 30 K,

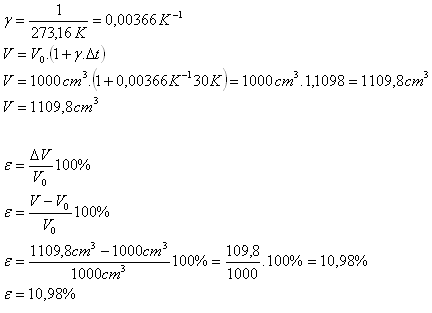
fyzika-tepelna-roztaznost-10.gif 

  • Das Volumen der Luft bei 400C ist V = 1109,8 cm3.
  • Die relative Volumenänderung ist ε = 10,98%.

11.Ein Student namens „Mistaken“ behauptete, dass aus der Beziehung l = l0(1 + αΔt) folge, dass bei hinreichend großer Abkühlung die Länge „l“ eines Stabes Null werde. Könnte er recht haben? Gegen welches wichtige Naturgesetz verstößt diese Behauptung?

Lösung:

Die Länge des Stabes ist Null, wenn:

l=0

l0(1+αΔt)=0

l0≠0⇒1+αΔt=0l_0 \neq 0 \Rightarrow 1 + \alpha \Delta t = 0

αΔt=−1\alpha \Delta t = -1

Δt=−1α\Delta t = -\dfrac{1}{\alpha}

Zum Beispiel für Kupfer (α=1.7×10−5 K−1\alpha = 1.7 \times 10^{-5}\ \text{K}^{-1}) ergibt sich:

Δt=−11.7×10−5 K=−58824 K\Delta t = -\frac{1}{1.7 \times 10^{-5}\ \text{K}^{-1}} = -58824\ \text{K

Ein Kupferstab müsste um 58 824 K abgekühlt werden. Eine so niedrige Temperatur existiert im Universum nicht. Die niedrigste mögliche Temperatur (noch nicht erreicht) ist 0 K = -273,150C — Absoluter Nullpunkt.