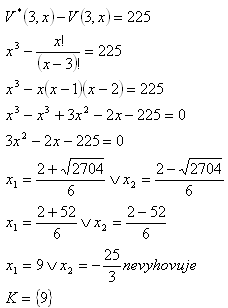Permutationen (allgemein)
1.Definieren und charakterisieren Sie Permutationen und Permutationen mit Wiederholungen.
Lösung:
Permutationen
Eine Permutation ist eine geordnete Folge von k Elementen, die aus einer gegebenen endlichen Menge von n Zahlen ohne Wiederholungen ausgewählt wird, wobei nicht unbedingt alle n Elemente der gegebenen Menge verwendet werden müssen.
Anzahl der möglichen Permutationen:
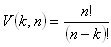
Permutationen mit Wiederholungen
Eine Permutation ist eine geordnete Folge von k Elementen, die aus einer gegebenen endlichen Menge von n Zahlen mit Wiederholungen ausgewählt wird, wobei nicht unbedingt alle n Elemente der gegebenen Menge verwendet werden müssen.
Anzahl der möglichen Permutationen mit Wiederholungen:
V*(k,n) = nk
2. Aus einer gegebenen Menge M = {a,b,c,d} alle Permutationen mit und ohne Wiederholung für k=2 auflisten. Bestimmen Sie ihre Anzahl.
Lösung:
a) Permutationen:
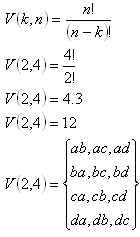
b) Permutationen mit Wiederholung:
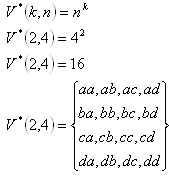
3. Es gibt 7 Mitglieder in einem Ausschuss. Auf wie viele Arten kann man einen Vorsitzenden, einen stellvertretenden Vorsitzenden, einen Sekretär und einen Kassierer wählen?
Lösung:
Permutationen, n = 7, k = 4
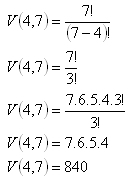
Es gibt 840 Möglichkeiten, die vier Funktionäre zu wählen.
4.Acht Schüler versprachen, sich gegenseitig eine Postkarte zu schicken. Wie viele Postkarten haben sie insgesamt verschickt?
Lösung:
Permutationen, n = 8, k = 2
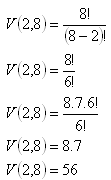
Die Schüler haben 56 Postkarten verschickt.
5.Aus wie vielen Zahlen können 240 Permutationen gebildet werden, wenn die Anzahl der zu wählenden Elemente 2 beträgt?
Lösung:
Permutationen, n = x, k = 2
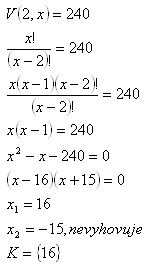
Es werden 16 Zahlen benötigt.
6.Wenn die Anzahl der Mitglieder um 2 zunimmt, steigt die Anzahl der möglichen Variationen mit k=3 um 384. Wie viele Mitglieder gibt es?
Lösung:
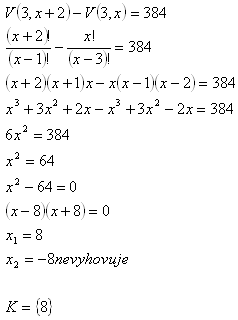
Es gibt 8 Mitglieder.
7. Sie haben 6 verschiedene Lose in Ihrer Tasche, nummeriert von 1 bis 6. Auf wie viele Arten können Sie 3 davon auswählen (unter Berücksichtigung der Reihenfolge), wenn
a) das ausgewählte Los nicht in die Tasche zurückgelegt wird.
b) das ausgewählte Los in die Tasche zurückgelegt wird.
Lösung:
a)
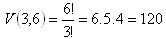
b)
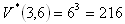
Die Lose können auf 120 bzw. 216 Arten ausgewählt werden.
8.Die Anzahl der Permutationen ohne Wiederholung mit k=3 aus x Mitgliedern ist um 225 kleiner als die Anzahl der Permutationen mit Wiederholung mit k=3 aus x Mitgliedern. Wie viele Mitglieder gibt es?
Lösung: