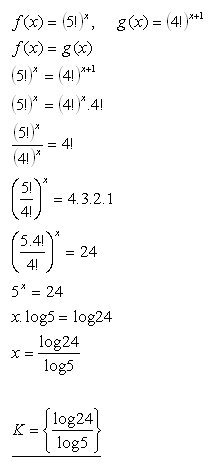Funktionsmerkmale

1. Was erinnerst du dich über die Eigenschaften von Funktionen?

Lösung:

Eine Funktion f einer reellen Variablen x ist eine Vorschrift, die jedem x ∈ R höchstens ein y ∈ R zuordnet, so dass
y = f(x)

Die Definitionsmenge der Funktion D ist die Menge aller x ∈ R, für die es genau ein y ∈ R gibt, so dass
y = f(x).

Die Wertemenge der Funktion H ist die Menge aller y ∈ R, für die es mindestens ein x ∈ R gibt, so dass
y = f(x).

$x_{2} > x_{1}, f (x_{2}) > f (x_{1})$ , dann ist die Funktion streng monoton steigend
$x_2 > x_1, f(x_2) < f(x_1)$ , dann ist die Funktion streng monoton fallend
$x_2 > x_1, f(x_2) \leq f(x_1)$ , dann ist die Funktion monoton fallend
$x_2 > x_1, f(x_2) \geq f(x_1)$ , dann ist die Funktion monoton steigend
$x_2 \neq x_1, f(x_2) \neq f(x_1)$ , dann ist die Funktion injektiv

Wenn es ein $h \in$ gibt, so dass $f (x) \leq h$ , dann ist die Funktion nach oben beschränkt
Wenn es ein $d \in$ gibt, so dass $f(x) \g$ , dann ist die Funktion nach unten beschränkt
Wenn die Funktion nach oben und nach unten beschränkt ist, ist sie beschränkt

Wenn $f(x + kp) = f(x)$ , dann ist die Funktion periodisch ( $p =$ Periode)
Wenn $f (- x) = f$ , dann ist die Funktion gerade
Wenn $f(-x) = -f(x)$ , dann ist die Funktion ungerade

Eine Funktion $f(x)$ besitzt eine Umkehrfunktion $f^{-1}(x)$ . Es gilt:
$D^{-} = H, H^{-} = D$

Zwei Funktionen sind gleich: f(x) = g(x), wenn: D(f) = D(g)

f(x) = g(x)

Welche der folgenden Graphen stellen Funktionen dar?
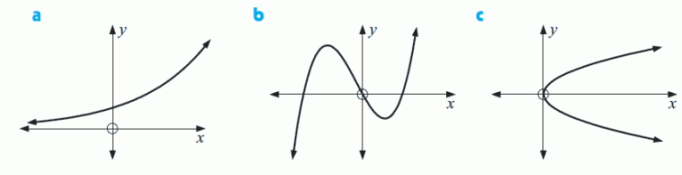
properties-of-functions-1az

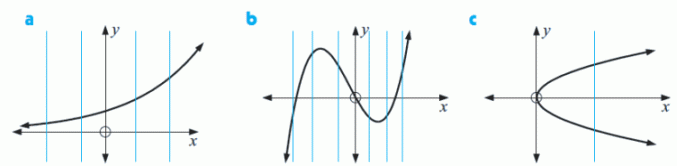
properties-of-functions-1ar

Funktion Funktion Keine Funktion

2.Bestimmen Sie, ob die folgenden Ausdrücke Funktionen sind:

Lösung:

A)
$y^2 = x \Rightarrow y = \sqrt{x}$ , Wenn $x = 1$ , dann $y_{1} = - 1$ oder $y_2 = 1$

Der Ausdruck ist keine Funktion.

B)
$y + ∣ x - 1 ∣ = 0$
$y - x + 1 = 0$ oder $y + x - 1 = 0$
$y = x - 1$ und $x \ge 1$
$y = 1 - x$ , $x \leq 1$

Der Ausdruck stellt zwei Funktionen dar.

Für $x \in (-\infty; 1]$ : $y = -x + 1$
Für $x \in (1; + \infty)$ : $y = x - 1$

C)
$∣ y - 1 ∣ + x = 0$
$y - 1 + x = 0$ oder $-y + 1 + x = 0$
$y = 1 - x$ $y = 1 + x$

Wenn $x = 5$ , dann $y_{1} = - 4$ und $y_2 = 6$
Der Ausdruck ist keine Funktion.

D)
$x y - 3 y = x^{2} - 9$
$y(x - 3) = (x - 3)(x + 3)$
$y = x + 3$ , falls $x \neq 0$ , dann $y = 3$

Der Ausdruck ist eine Funktion.

3.Entscheiden Sie, ob die folgenden Funktionen gleich sind:

Lösung:

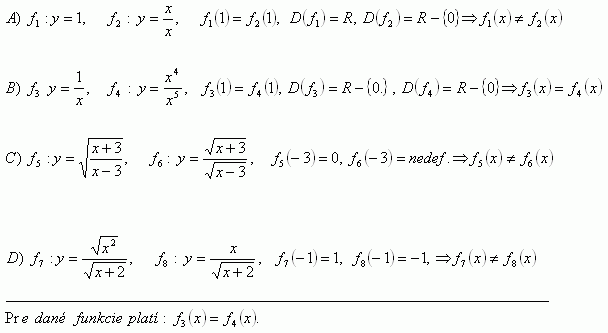
properties-of-functions-3r

Für die gegebenen Funktionen gilt: f₃(x) = F₄(X)

4.Bestimmen Sie die Geradheit oder Ungeradheit der Funktionen:

Lösung:

funktion-4-r

5. Bestimmen Sie, welche der folgenden Funktionen in der gegebenen Definitionsmenge beschränkt sind.

Lösung:

funktion-5-r-a

funktion-5-r-b

6. Bestimmen Sie für die gegebenen Funktionen die Umkehrfunktionen.

Lösung:

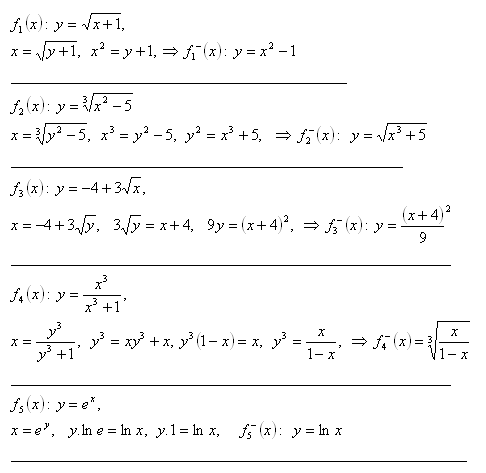
properties-of-functions-6r

7.Bestimmen Sie die Umkehrfunktion für die Funktionen:

Lösung:

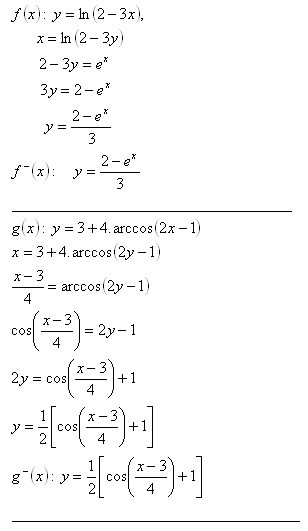
properties-of-functions-7r

8. In der Funktion f(x): y = ax² + bx + c , x ∈ R, bestimmen Sie a, b, c ∈ R, so dass f(0) = -3, f(-1) = -6, f(2) = 15.

Lösung:

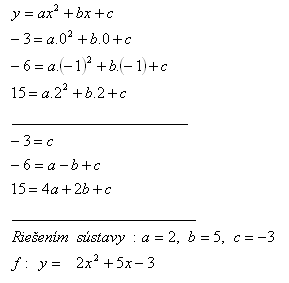
properties-of-functions-8

Die Lösung des Gleichungssystems ist a=2, b=5, c=-3

f: y=2x² + 5x -3

9. Bestimmen Sie b, d der Funktion f: y = (x + b):(x + d) so, dass f(1) = -1, f(-1) = -1/3

Lösung:

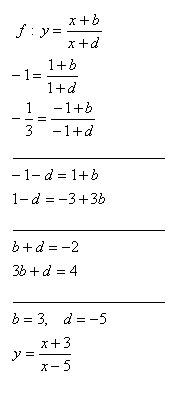
properties-of-functions-9

10.Bestimmen Sie die Menge aller Funktionen f(x), für die Folgendes gilt:

Lösung:

Die Funktion ist fallend und daher gilt

Die Menge besteht aus allen Funktionen f(x): y= 2/(x-a)

11.Die Funktion f: y= -2x +3 ist gegeben

a.) Bestimmen Sie f(0), f(-5)
b.) Für welche x gilt f(x) = 1, f(x) = -5
c.) Bestimmen Sie die Schnittpunkte des Graphen der Funktion mit den Koordinatenachsen

Lösung:

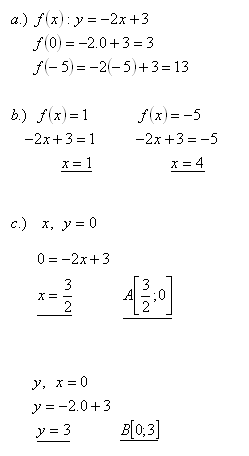
properties-of-functions-11

12.Geben Sie eine lineare Funktion an, deren Graph durch die Punkte verläuft

Lösung:

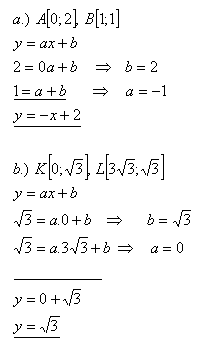
properties-of-functions-12r

Die Gleichungen der Funktionen sind: f₁: y = – x + 2 und f₂: y = √3.

13.Laut Autohersteller ist der Kraftstoffverbrauch eines Autos pro 100 km wie folgt. Bei einer Geschwindigkeit von 80 km/h verbraucht es 6 Liter Kraftstoff, bei einer Geschwindigkeit von 110 km/h verbraucht es 8,1 Liter. Bestimmen Sie den Verbrauch des Autos bei einer Geschwindigkeit von 90 km/h.

Lösung:

x = Geschwindigkeit, y = Verbrauch

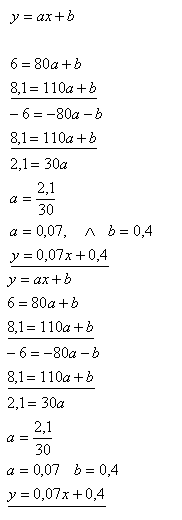
properties-of-functions-13-1

Verbrauch bei einer Geschwindigkeit von 90 km/h.

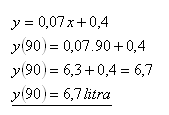
properties-of-functions-13-2

Der Kraftstoffverbrauch des Autos bei einer Geschwindigkeit von 90 km/h beträgt 6,7 Liter pro 100 Kilometer.

14.Die Funktion f: y = x² - 4x -12 ist gegeben.

a.) Bestimmen Sie, für welche x gilt, dass f(x) = 9
b.) Bestimmen Sie die Schnittpunkte des Graphen der Funktion mit den Koordinatenachsen

Lösung:

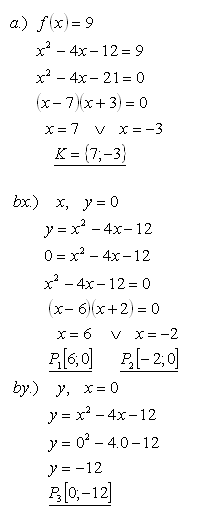
15.Geben Sie eine quadratische Funktion an, deren Elemente die geordneten Paare sind

A[0;1], B[2;-1], C[1;-1]

Lösung:

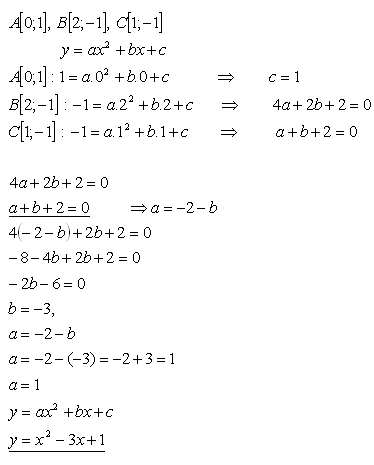
properties-of-functions-15

Die quadratische Funktion hat die Gleichung: f : y = x² - 3x +1

16.Die quadratische Funktion f: y = x² – 3x + c ist gegeben. Bestimmen Sie c so, dass die Funktion

a.) keinen gemeinsamen Punkt mit der x-Achse hat
b.) genau einen gemeinsamen Punkt mit der x-Achse hat
c.) genau zwei gemeinsame Punkte mit der x-Achse hat

Lösung:

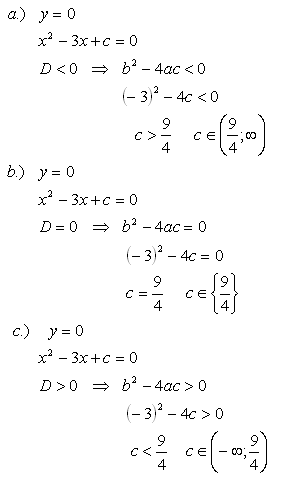
17.Die quadratische Funktion f: y = x² + 4x – 5 ist gegeben. Bestimmen Sie ihre Schnittpunkte mit den Koordinatenachsen und den Scheitelpunkt ihres Parabelgraphen.

Lösung:

Mit der x-Achse: y = 0 Mit der y-Achse : x = 0

18.Bestimmen Sie die Koeffizienten a, b, so dass der Graph der Funktion f: y = a·log x + b durch die Punkte K, L verläuft, wobei gilt:

Lösung:

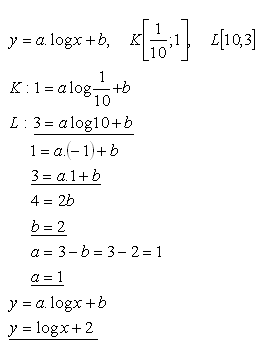
Die Gleichung der logarithmischen Funktion lautet: y = log x + 2.

19.Bestimmen Sie die Koeffizienten a, b, so dass die Funktion f: y = a^2x + b durch den Ursprung des Koordinatensystems und den Punkt M [1; 1] verläuft.

Lösung:

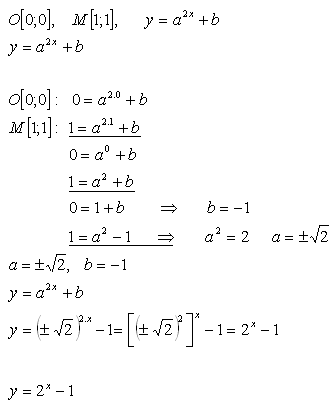
Die Funktion hat die Form f: y = 2^x − 1.

20.Für welche reellen Zahlen x nehmen die Funktionen f(x) = (5!)^x und g(x) = (4!)^x+1 dieselben Werte an?

Lösung:

Mathematik

Funktionsmerkmale

Adblock detected