sk|cz|en|

Physik

Leiterkapazität

1.Erkläre den Begriff „Leiterkapazität“!

Lösung:

Kapazität eines Leiters CC ist die Fähigkeit eines Leiters, elektrische Ladung zu binden und zu verteilen.

C=QUC = \frac{Q}{U} [C]=C⋅V−1=1F=farad[C] = C \cdot V^{-1} = 1F = farad

Q=Q = Ladung im elektrischen Feld des Leiters
U=U = Spannung des Leiters

Kapazität eines Plattenkondensators:

C=ε0⋅εr⋅SlC = \frac{\varepsilon_0 \cdot \varepsilon_r \cdot S}{l}

l=l = Abstand zwischen den Platten, S=S = wirksame Fläche der Kondensatorplatten.
ε0=8.854⋅10−12 C2⋅N−1⋅m−2 (F⋅m−1)\varepsilon_0 = 8.854 \cdot 10^{-12} \, C^2 \cdot N^{-1} \cdot m^{-2} \, (F \cdot m^{-1}), Permittivität des Vakuums.
εr=\varepsilon_r = relative Permittivität des Mediums zwischen den Kondensatorplatten.

Kapazität einer Kugel:

C=4πε0εrRC = 4 \pi \varepsilon_0 \varepsilon_r R

Energie des elektrischen Feldes eines geladenen Kondensators:

Ee=12CU2=12Q2CE_e = \frac{1}{2} C U^2 = \frac{1}{2} \frac{Q^2}{C}

Reihenschaltung von Kondensatoren:

1C=1C1+1C2+1C3+…+1Cn\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \ldots + \frac{1}{C_n}

Parallelschaltung von Kondensatoren:

C=C1+C2+C3+…+CnC = C_1 + C_2 + C_3 + \ldots + C_n

 

2.Leite die Dimension der physikalischen Einheit Farad = F her. Zeige, dass gilt: C2·N−1·m−2 = F·m−1

Lösung:

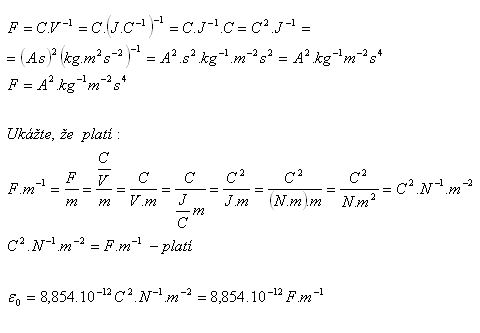
 fyzika-kapacita-vodica-2.gif

Damit ist gezeigt, dass 1 F = A2·kg−1·m−2·s4 und dass C2·N−1·m−2 = F·m−1 gilt.

3.Berechne die Kapazität eines Plattenkondensators, der aus 11 Platten mit den Abmessungen 3 cm und 2 cm besteht, wenn der Abstand zwischen den Platten 0,2 mm beträgt. Das Dielektrikum zwischen den Platten ist Glimmer mit εr = 6. Zwischen den 11 Platten befinden sich 10 Spalte.

Lösung:

Analyse:

S = a·b = 3 cm·2 cm = 6 cm2 = 6·10−4 m2,  l = 2·10−4 m,  εr = 6, ε0 = 8,854·10−12 C2·N−1·m2

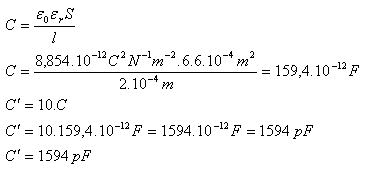
fyzika-kapacita-vodica-3.gif 

Die Kapazität des Kondensators beträgt C' = 1594 pF.

4.Wie groß ist die Spannung zwischen den Platten eines Luftkondensators mit zwei quadratischen Platten der Seitenlänge 10 cm, die durch 2 cm getrennt sind, wenn seine Ladung 8,854·10–3 μC beträgt?

Lösung:

Analyse:

S = a2 = (10 cm)2 = 100 cm2 = 10−2 m2,  l = 2·10–2 m,  Q = 8,854·10–9 C, ε0 = 8,854·10–12 F·m−1

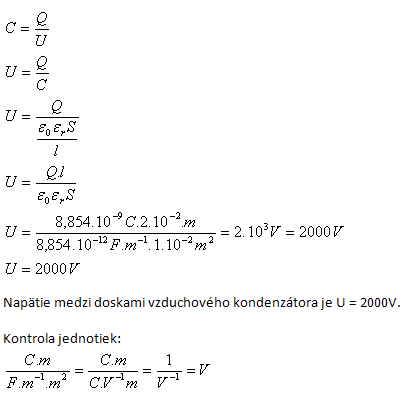
fyzika-kapacita-vodica-4.gif

5.Wie groß ist die Kapazität unserer Erde?

Lösung:

Analyse:

R = 6378 km = 6,378·106 m, ε0 = 8,854·10−12 F·m−1, εr = 1

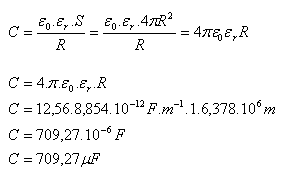
fyzika-kapacita-vodica-5.gif 

Die Kapazität der Erde ist C = 709,27 μF.