Dreieck
1.Charakterisiere ein Dreieck
Lösung:
– Innenwinkel:
α + β + γ = 180°
– Außenwinkel:
α′ + β′ + γ′ = 360°
– Innen- und Außenwinkel:
α + α′ = 180°, β + β′ = 180°, γ + γ′ = 180°
– Radius des Inkreises:
p = 4r sin(α/2) sin(β/2) sin(γ/2)
r – Radius des Inkreises
– Sinussatz:
a / sin α = b / sin β = c / sin γ = 2r, r – Radius des Inkreises
– Kosinussatz:
a² = b² + c² – 2bc cos α
b² = a² + c² – 2ac cos β
c² = a² + b² – 2ab cos γ
– Umfang:
O = a + b + c, s = (a + b + c) / 2
– Fläche:
S = (a·vₐ) / 2 = (b·v_b) / 2 = (c·v_c) / 2
S = (a·b·sin γ) / 2 = (a·c·sin β) / 2 = (b·c·sin α) / 2
S = p·s
S = (a·b·c) / (4ρ)
S = √[s(s – a)(s – b)(s – c)] (Heronsche Formel)
S = 2r²·sin(α/2)·sin(β/2)·sin(γ/2)
2.Beweise für die Außenwinkel eines Dreiecks: α*+ β*+ γ* = 360°.
Beweis:
α + α* = 180°
β + β* = 180°
γ + γ* = 180°
_____________
α + β + γ + α* + β* + γ* = 540°
α* + β* + γ* = 540° – (α + β + γ)
α* + β* + γ* = 540° - 180°
α* + β* + γ* = 360°
3. Eine Seite des Dreiecks hat die Länge c = 10 cm. Für seine Winkel gilt: α:β:γ = 3:5:10.
Bestimme:
a) Umfang
b) Fläche
Lösung:
Umfang
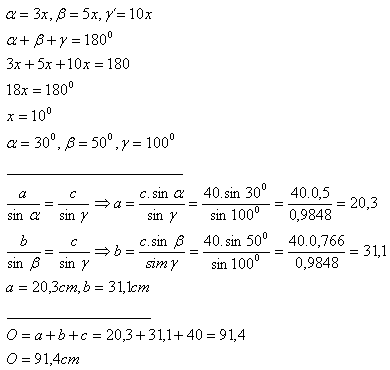
Fläche
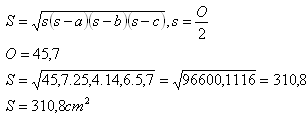
4.Die Seitenlänge eines gleichseitigen Dreiecks beträgt a = 10 cm.
Bestimme die Fläche zwischen dem Umkreis und dem Inkreis.
Lösung:
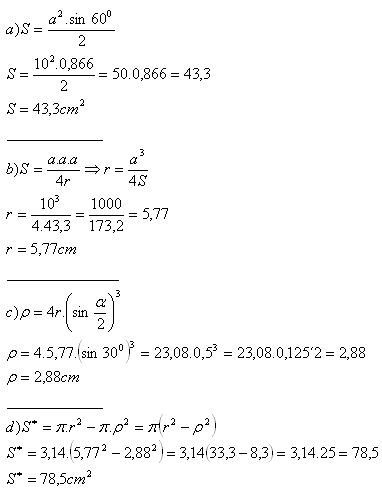
5.Johann steht 5 m und 8 m von den Enden eines Baumes entfernt. Er sieht den Baum unter einem Winkel von 60°.
Bestimme die Höhe des Baumes.
Lösung:
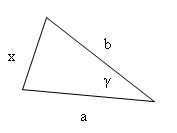
a = 5 m
b = 8 m
γ = 60°
x
2 = a
2 + b
2 -2ab·cosγ
x
2 = 5
2 + 8
2 -2·5·8·cos60°
x
2 = 25 + 64 – 80·0,5
x
2 = 25 + 64 – 40
x
2 = 49
x = 7
Der Baum ist 7 m hoch.
6.Drei Tangentialkreise mit den Radien r1 = 2 cm, r2 = 3 cm, r3 = 4 cm. Die Mittelpunkte der Kreise bilden ein Dreieck.
Bestimme die Innenwinkel des Dreiecks.
Lösung:
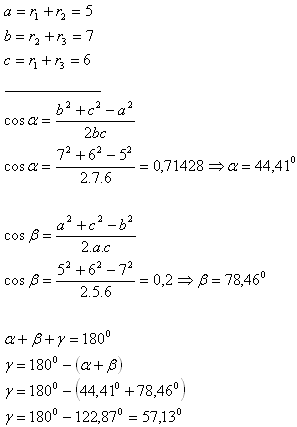
Die Innenwinkel des Dreiecks sind α = 44,41°, β = 78,46° und γ = 57,13°.
7.Zwei Züge verlassen gleichzeitig den Bahnhof auf zwei Gleisen, die den Winkel φ = 156° bilden. Ihre Geschwindigkeiten sind v1 = 13 m/s, v2 = 14,5 m/s.
Bestimme ihren Abstand nach der Zeit t = 5 min.
Lösung:
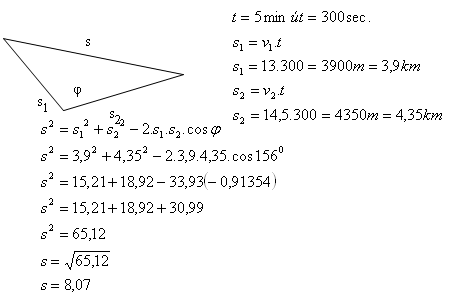
Der Abstand zwischen den Zügen nach 5 Minuten beträgt 8,07 km.
8.Die Kräfte F1, F2 greifen im selben Punkt an. Der Winkel zwischen den Kräften beträgt φ = 60°.
Bestimme die Größe der resultierenden Kraft, wenn F1 = 42 N, F2 = 35 N.
Bestimme die Winkel zwischen den Kräften F1, F2 und der resultierenden Kraft.
Lösung:
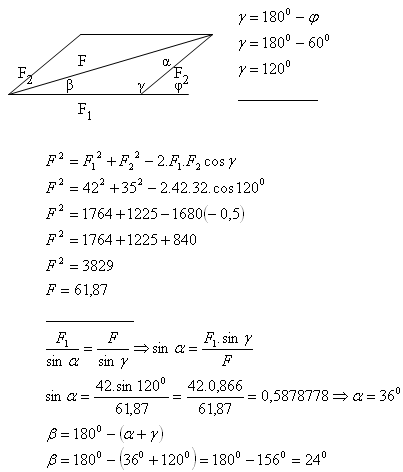
Die resultierende Kraft beträgt F = 61,87 N.
Die Winkel sind α = 36° und β = 24°.
9.Der Winkel zwischen den Ufern eines Flusses, beobachtet von einem 20 m hohen Turm, der 20 m vom Fluss entfernt steht, beträgt 15°.
Bestimme die Breite des Flusses.
Lösung:
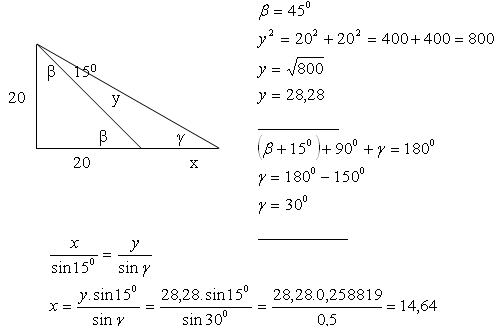
Die Breite des Flusses beträgt x = 14,64 m.
10. Ein Körper mit der Masse m = 1563 kg hängt an einem waagerechten Träger. Er ist mit zwei unterschiedlich langen Seilen befestigt. Die Winkel zwischen den Seilen und dem Träger betragen α = 48°, β = 62°.
Bestimme die Kräfte, die auf die Seile wirken. (F = 15630 N)
Lösung:
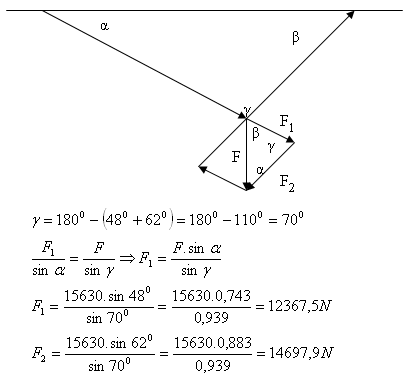
Die Kräfte, die auf die Seile wirken, sind F
1 = 12367,5 N und F
2 = 14697,9 N.