sk|cz|en|

Physik

Arbeiten in einem elektrischen Feld

1. Charakterisieren Sie die physikalischen Größen: Arbeit im elektrischen Feld, elektrisches Potenzial und elektrische Spannung.

Lösung:

A)
Die Arbeit im elektrischen Feld ist die Arbeit äußerer Kräfte beim Bewegen einer Ladung im elektrischen Feld.

W=E⋅Q0⋅dW = E \cdot Q_0 \cdot d

E=E = elektrische Feldstärke, Q0=Q_0 = verschobene Ladung,
d=d = Wegstrecke, um die die Ladung bewegt wird

[W]=1J[W] = 1J

B)
Das elektrische Potenzial an einem gegebenen Punkt im elektrischen Feld ist das Verhältnis der von den elektrischen Kräften des Feldes verrichteten Arbeit beim Transport eines Teilchens mit der Ladung Q0Q_0 von diesem Punkt zum Punkt des Nullpotenzials zur Ladung Q0Q_0.

φ=WQ0=EyQ=k⋅Qr=E⋅d\varphi = \frac{W}{Q_0} = \frac{E_y}{Q} = \frac{k \cdot Q}{r} = E \cdot d [φ]=1J⋅C−1=1V=volt[\varphi] = 1J \cdot C^{-1} = 1V = volt

C)
Die elektrische Spannung zwischen zwei verschiedenen Punkten des elektrischen Feldes ist gleich dem Betrag der Differenz der Potenziale zwischen diesen Punkten des elektrischen Feldes.

U=∣φ1−φ2∣=WQ0=E⋅dU = |\varphi_1 - \varphi_2| = \frac{W}{Q_0} = E \cdot d [U]=1V[U] = 1V

 

2.Welche Arbeit verrichtet ein elektrisches Feld mit der Feldstärke 104N·C-1, wenn es eine Ladung von 20 μC entlang der Feldlinie über eine Strecke von 10 cm bewegt?

Lösung:

Analyse:

E = 104N·C-1,  Q0 = 20 μC  = 20·10-6C,  d = 10 cm = 10-1m

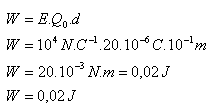
fyzika-praca-v-elektrickom-poli-2.gif 

Das elektrische Feld verrichtet die Arbeit W = 0,02 J.

3.Welches Potenzial hat ein Leiter, wenn für das Überführen einer Ladung von 50 μC von einem Punkt mit Nullpotenzial auf seine Oberfläche eine Arbeit von 0,2 J erforderlich war?

Lösung:

Analyse:

Q0 = 50·10-6C, W = 2·10-1J,  φ = ?

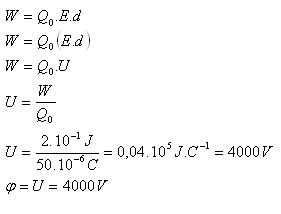
fyzika-praca-v-elektrickom-poli-3.gif 

Der Leiter hat das Potenzial φ = 4000 V.

4.In einem homogenen elektrischen Feld mit der Feldstärke 1 kV·m-1 bewegt sich ein Teilchen mit der Ladung 25·10-9C entlang eines Weges von 2 m.

  • a) Welche Arbeit verrichten die Kräfte des elektrischen Feldes beim Bewegen des Teilchens?
  • b) Wie groß ist die elektrische Spannung zwischen Start- und Endpunkt der Verschiebung?

Lösung:

Analyse:

E = 103 V·m-1,  Q0 = 25·10-9C,  d = 2 m ,  W = ?  U = ?

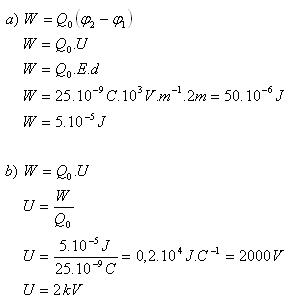
fyzika-praca-v-elektrickom-poli-4.gif 

  • Die Feldkräfte verrichten die Arbeit W = 5·10-5J.
  • Die Spannung zwischen Start- und Endpunkt der Verschiebung beträgt U = 2 kV.

5.Welche Geschwindigkeit erreicht ein Elektron (Qe= 1,602·10-19C, me = 9,1·10-31kg), wenn es eine Potentialdifferenz von 100 V durchläuft?

Lösung:

Analyse:

Qe= 1,602·10-19C, me = 9,1·10-31kg,  Δφ = U = 100 V = 102V

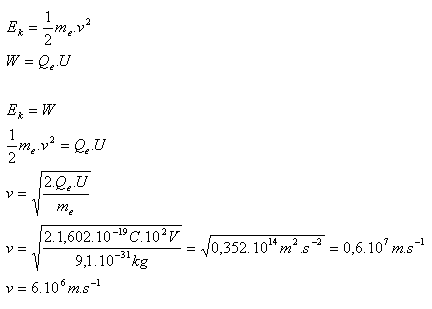
fyzika-praca-v-elektrickom-poli-5.gif 

Das Elektron erreicht die Geschwindigkeit v = 6·106 m·s-1.

6.Bestimmen Sie die elektrische Feldstärke zwischen zwei parallelen Leitplatten, die 5 cm voneinander entfernt sind, wenn die Spannung zwischen ihnen 150 V beträgt. Welche Arbeit verrichten die Feldkräfte beim Überführen einer Ladung von 1 μC von der einen Platte zur anderen?

Lösung:

Analyse:

d = 5 cm = 5·10-2m,  U = 150 V,  Q0 = 1 μC = 10-6C,  E = ?,  W = ?

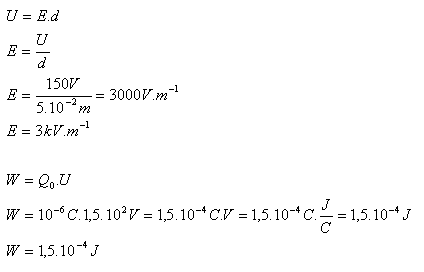
fyzika-praca-v-elektrickom-poli-6.gif 

Die elektrische Feldstärke zwischen den beiden parallelen Leitplatten ist E = 3 kV·m-1. Die Feldkräfte verrichten die Arbeit W = 1,5·10-4J.

7.Ein Alphateilchen ( mα = 6,7·10-27kg, Q0α = 3,2·10-19C) trat mit der Geschwindigkeit 2·106 m·s-1 in ein homogenes elektrisches Feld ein. Das Teilchen kam nach 2 m zum Stillstand.

  • Welche Potentialdifferenz hat das Teilchen durchlaufen?
  • Wie groß ist die elektrische Feldstärke?

Lösung:

Analyse:

mα = 6,7·10-27kg, Q0α = 3,2·10-19C,  v = 2·106 m·s-1,  d = 2 m,  U = ?, E = ?

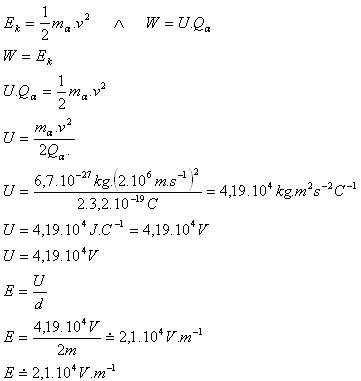
fyzika-praca-v-elektrickom-poli-7.gif 

  • Das Teilchen hat die Potentialdifferenz Δφ = U = 4,19·104 V durchlaufen.
  • Die elektrische Feldstärke ist E = 2,1·104 V·m-1.

8.Welche elektrische Ladung hat ein mikroskopischer Öltropfen der Masse 6,4·10-16kg, wenn er zwischen den Platten eines geladenen Kondensators schwebt? Die Kondensatorplatten sind 1 cm voneinander entfernt und die Spannung zwischen ihnen beträgt 400 V. (Experiment R.A. Millikan)

Lösung:

Analyse:

m = 6,4·10-16kg,  d = 1 cm = 10-2m,  U = 4·102V,  g = 10 m·s-2,  Q = ?

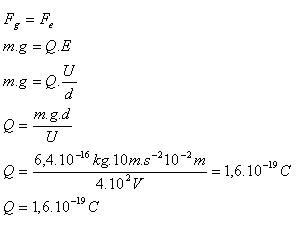
fyzika-praca-v-elektrickom-poli-8.gif 

Die elektrische Ladung des Öltropfens ist die Elementarladung Q = 1,6·10-19C.

9.Welche Arbeit verrichten die Kräfte des elektrischen Feldes, das durch die Ladung Q = 2 μC erzeugt wird, wenn die Ladung Q0 = 1 nC von einem Punkt im Abstand 10 cm von Q zu einem Punkt im Abstand 20 cm von Q bewegt wird?

Lösung:

Analyse:

Q = 2 μC = 2·10-6C,  Q0 = 1 nC = 10·10-9C,  r1 = 0,1 m,  r2 = 0,2 m, k = 9·109 N·m2·C-2

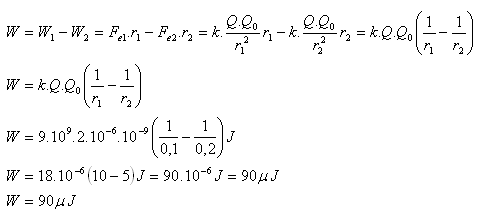
fyzika-praca-v-elektrickom-poli-9.gif 

Die Kräfte des elektrischen Feldes verrichten die Arbeit W = 90 μJ.

10.Ein Elektron (e = 1,602·10-19C) bewegt sich in einem homogenen elektrischen Feld von einem Potentialniveau von 200 V auf ein Niveau von 300 V. Die Anfangsgeschwindigkeit ist null, die Endgeschwindigkeit beträgt 5,93·106 m·s-1. Bestimmen Sie:

  • die Zunahme der Energie des Elektrons beim Durchgang zwischen den beiden Potentialniveaus
  • die Masse des Elektrons

Lösung:

Analyse:

e = 1,602·10-19C,  U = Δφ = 100 V,  v0 = 0,  v = 5,93·106 m·s-1

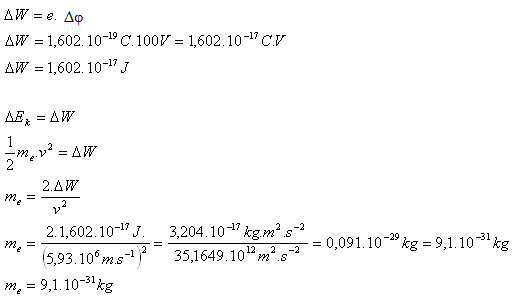
fyzika-praca-v-elektrickom-poli-10.gif 

  • Die Zunahme der Energie des Elektrons beträgt ΔW = 1,602·10-17J.
  • Die Masse des Elektrons ist me = 9,1·10-31kg.