Viereck
1. Charakterisiere die Vierecke:
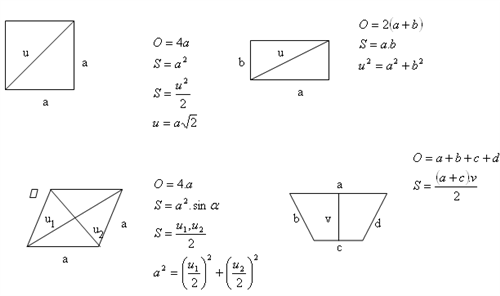
- Quadrat
- Rechteck
- Rhombus
- Trapez
Lösung:
2. In einem Rhombus mit der Fläche S = 864 cm2 ist eine Diagonale 12 cm kürzer als die andere.
Bestimme die Längen der Diagonalen und die Seite des Rhombus.
Lösung:
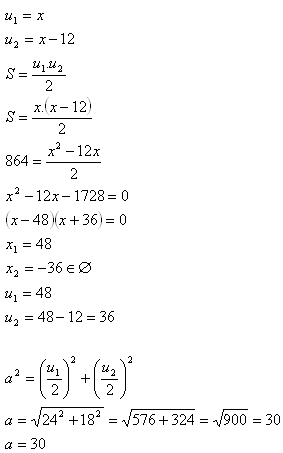
Im Rhombus sind die Diagonalen u
1 = 48 cm, u
2 = 36 cm.
Seite a = 30 cm.
3. Ein Rechteck hat einen Umfang O = 46 cm und eine Diagonale u = 17 cm.
Berechne seine Fläche.
Lösung:
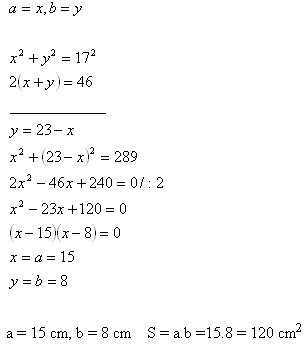
4. Ein Rhombus hat die Diagonalen u1 = 6 cm, u2 = 8 cm.
Berechne seine Innenwinkel.
Lösung:
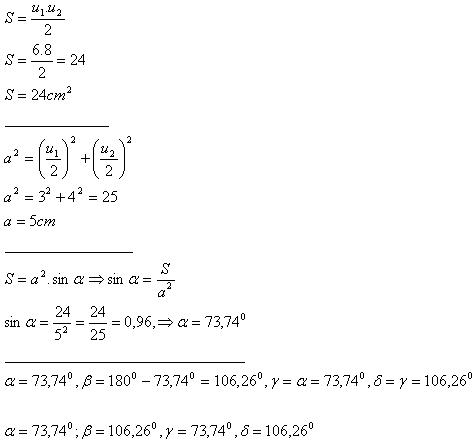
5. Ein regelmäßiges Sechseck ist in einen Kreis mit Radius r eingeschrieben.
Leite die Formel für den Umfang und die Fläche eines regelmäßigen Sechsecks her. (r = a)
Wie lang ist die Seite eines regelmäßigen Sechsecks mit der Fläche S = 93,42 cm2?
Lösung:
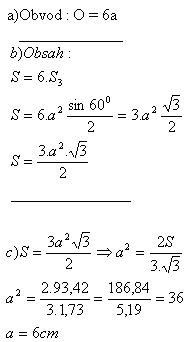
Die Seite des regelmäßigen Sechsecks ist a = 6 cm.
6. Ein gleichschenkliges Trapez hat die untere Basis c = 2,9 cm, die Höhe v = 7,5 cm und den Winkel α = 35°.
Berechne seine Fläche und seinen Umfang.
Lösung:
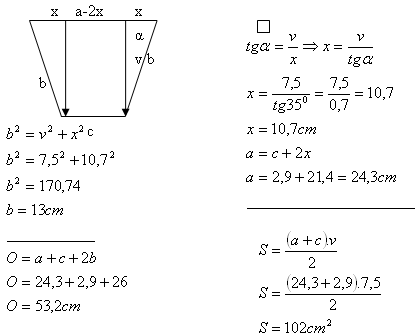
Der Umfang des gleichschenkligen Trapezes beträgt 53,2 cm und die Fläche beträgt 102 cm
2.
7. Das Trapez ABCD hat eine Fläche S = 7,2 cm2, Basen AB = 1,4 cm, CD = 0,6 cm.
Berechne die Fläche des Dreiecks ΔACD.
Lösung:
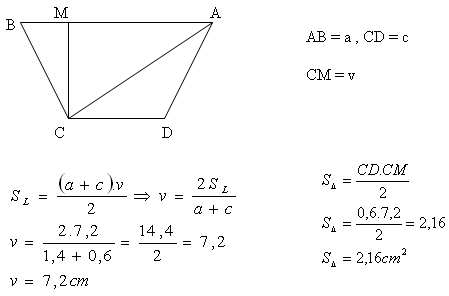
Die Fläche des Dreiecks ΔABC ist S = 21,6 cm
2.
8. Die Höhe und die parallelen Seiten eines Trapezes stehen im Verhältnis v:a:c = 2:3:5, und seine Fläche beträgt S = 512 cm2.
Berechne die Höhe und die parallelen Seiten.
Lösung:
v = 2x = 2·8 = 16
a = 3x = 3·8 = 24
c = 5x = 5·8 = 40
v = 16 cm, a = 24 cm, c = 40 cm
9. Ein Rechteck hat eine Diagonale u = 34 cm. Wenn jede seiner Seiten um 4 cm verlängert wird, vergrößert sich seine Fläche um 200 cm2.
Bestimme die Abmessungen des Rechtecks.
Lösung:
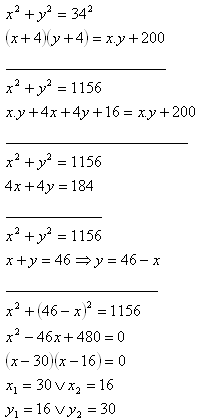
Die Abmessungen des Rechtecks sind a = 30 cm, b = 16 cm.
10. Ein Trapez hat eine obere Basis c = 33 cm und eine Höhe v = 15 cm. Die anderen drei Seiten sind gleich lang.
Berechne den Umfang des Trapezes.
Lösung:
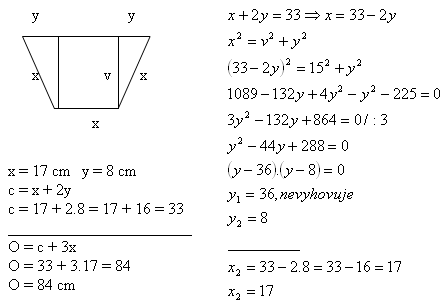
Der Umfang des Trapezes beträgt O = 84 cm.