Elektrischer Strom in Halbleitern
1. Der Thermistor hat einen Widerstand von 50 kΏ bei einer Temperatur von 200C und bei einer Temperatur von 250C verringert sich sein Widerstand auf 42,5 kΏ. Bestimmen Sie den durchschnittlichen Wert des Temperaturkoeffizienten des Widerstands in diesem Temperaturintervall.
Lösung:
Analyse:
Δt = 50C = 5 K, R20 = 50 000 Ώ, R25 = 42 500 Ώ, α = ?
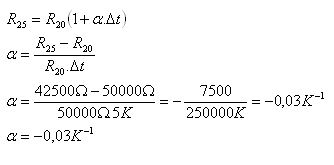
Der Temperaturkoeffizient des Widerstands des Thermistors beträgt α = –0,03 K–1
2.Der durchschnittliche Wert des Temperaturkoeffizienten des Widerstands eines Thermistors beträgt α = –0,05 K–1. Um wie viel muss sich die Temperatur des Thermistors erhöhen, damit sein Widerstand auf die Hälfte sinkt?
Lösung:
Analyse:
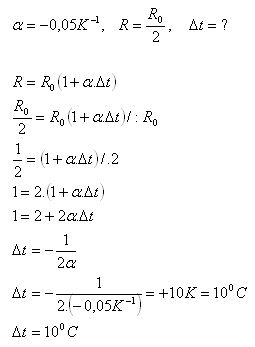
Die Temperatur des Thermistors muss um 100C steigen.
3.Ein in einem Stromkreis angeschlossener Thermistor wird durch die Flamme eines Gasbrenners erhitzt. Die Abhängigkeit des Widerstands des Thermistors von der Temperatur ist durch eine Tabelle gegeben. Wie hoch ist die Temperatur des Thermistors, wenn das Voltmeter 3 V und das Amperemeter 15 mA anzeigt?
Lösung:
Analyse:
U = 3 V, I = 15·10–3 A

Laut Tabelle hat der Thermistor einen Widerstand von 200 Ώ, wenn er auf eine Temperatur von 3000C erhitzt wird.
4.Ein NPN-Transistor ist in einem elektrischen Stromkreis angeschlossen. Wenn sich der Basisstrom von 0,2 mA auf 0,3 mA ändert, ändert sich der Kollektorstrom bei konstanter Kollektorspannung von 4,5 V von 5 mA auf 20 mA. Bestimmen Sie den Stromverstärkungsfaktor β des Transistors.
Lösung:
Analyse:
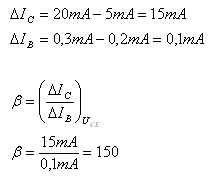
Der Stromverstärkungsfaktor des Transistors bei einer Spannung von 4,5 V beträgt β = 150.
5.Eine aus einem Silizium-Einkristall geschnittene Halbleiterprobe hat die Form eines Quaders mit einer Länge von 5 mm und einer Grundfläche von 4 mm2. Auf zwei gegenüberliegenden Flächen mit einer Fläche von 4 mm2 werden metallische Kontakte angebracht. Wenn zwischen den Kontakten eine Spannung von 4,5 V angelegt wird, fließt bei einer Temperatur von 200C ein Strom von 1,2 mA durch die Probe. Nach dem Erhitzen der Probe auf 3000C steigt der Strom auf 2,16 mA. Wie groß ist der spezifische Widerstand von Silizium bei 200C und 3000C? Bestimmen Sie auch den Temperaturkoeffizienten des elektrischen Widerstands α.
Lösung:
Analyse:
l = 5·10–3 m, S = 4·10–6 m2, U = 4,5 V, I20 = 1,2·10–3 A, I300 = 2,16·10–3 A, ρ20 = ?, ρ300 = ?
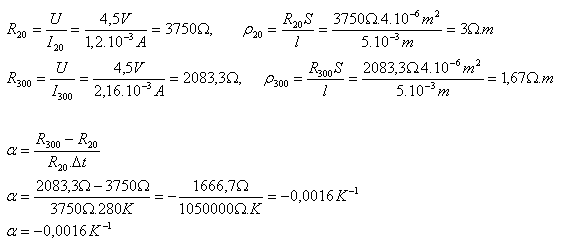
Der spezifische Widerstand von Silizium beträgt ρ20 = 3 Ώ·m und ρ300 = 1,67 Ώ·m.
Der Temperaturkoeffizient des elektrischen Widerstands von Silizium beträgt α = –0,0016 K–1