Würfel, Quader, Prisma und Zylinder
1. Gib die Grundformeln zur Berechnung von Volumen und Oberfläche an:
- Würfel
- Quader (Rechteckprisma)
- Prisma
- Zylinder
Lösung:
Würfel
a – Kante des Würfels
Volumen V = a
3
Oberfläche S = 6a
2
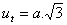 Quader
Quader
a, b, c – Kanten des Quaders
Volumen V = a·b·c
Oberfläche S = 2(ab+ac+bc)
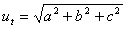 Prisma
Prisma
S
p – Grundfläche
Q – Mantelfläche
v – Höhe des Prismas
Volumen V = S
p·v
Oberfläche S = 2S
p + Q
Zylinder
r – Radius der Grundfläche
v – Höhe des Zylinders
Volumen V = π·r
2·v
Oberfläche S = 2πr(r+v)
Q = 2πrv
2. Zwei würfelförmige Kisten mit Kanten a = 70 cm, b = 90 cm sollen durch eine würfelförmige Kiste ersetzt werden.
Wie lang wird ihre Kante sein?
Lösung:
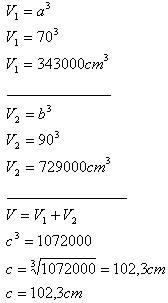
Die Kante des Ersatzwürfels beträgt c = 102,3 cm.
3. Die Kante des zweiten Würfels ist 2 cm länger als die des ersten. Der Unterschied ihrer Volumina beträgt 728 cm3.
Berechne die Kantenlängen beider Würfel.
Lösung:
Kante des ersten Würfels: x
Kante des zweiten Würfels: x + 2
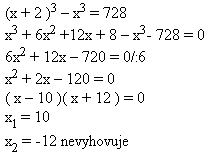
Die Kante des ersten Würfels ist 10 cm, die des zweiten 12 cm.
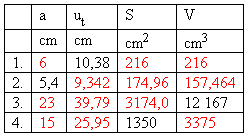
4. Ein Würfel mit der Kante a ist gegeben. Bekannte Werte stehen in der Tabelle.
Vervollständige die Tabelle!
Lösung:
5. Die Kanten zweier Würfel unterscheiden sich um 22 cm. Ihre Oberflächen unterscheiden sich um 19.272 cm2.
Bestimme die Kanten beider Würfel.
Lösung:
x – Kante des ersten Würfels
y – Kante des zweiten Würfels
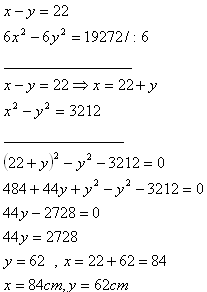
Die Kanten der Würfel sind x = 84 cm und y = 62 cm.
6. Ein Quader hat die Maße a = 4 cm, b = 3 cm, c = 5 cm.
Berechne den Winkel α zwischen der Basisdiagonale und der Raumdiagonale.
Lösung:
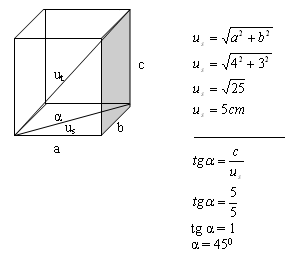
Der Winkel zwischen den Diagonalen beträgt α = 45°.
7. Die Oberfläche eines Quaders beträgt S = 376 cm2. Seine Kanten stehen im Verhältnis a:b:c = 3:4:5.
Berechne das Volumen dieses Quaders.
Lösung:
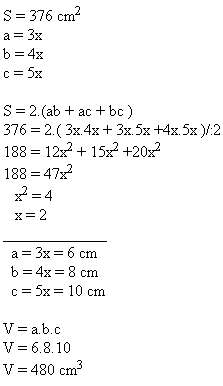
Das Volumen des Quaders beträgt V = 480 cm
3.
8. Ein Wasserbehälter in Form eines Quaders enthält 1500 hl Wasser; die Wasserhöhe beträgt 2,5 m.
Bestimme die Grundflächenabmessungen, wenn eine Seite 4 m länger als die andere ist.
Lösung:
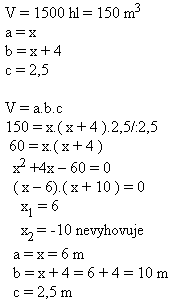
Die Grundmaße des Behälters sind a = 6 m, b = 10 m.
9. Berechne das Volumen eines Quaders, wenn seine Grundfläche S1 = 272 cm2 und seine Seitenflächen S2 = 240 cm2, S3 = 255 cm2 betragen.
Lösung:
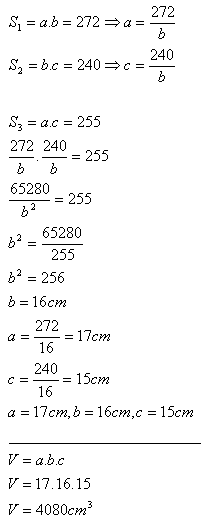
Das Volumen des Quaders beträgt 4080 cm
3.
10. Wie groß ist die Masse einer Eisenstange (ρ = 7800 kg·m-3), die 1,5 m lang ist und einen quadratischen Querschnitt mit der Seite a = 45 mm hat?
Lösung:
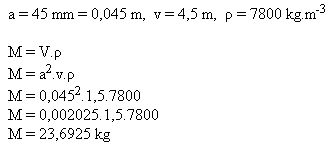
Die Masse der Eisenstange beträgt etwa M = 23,7 kg.
11. Die Basis eines geraden dreieckigen Prismas ist ein rechtwinkliges Dreieck mit Katheten a = 9 cm, b = 12 cm. Die Höhe des Prismas ist doppelt so groß wie die Hypotenuse der Basis.
Berechne das Volumen und die Oberfläche des Prismas.
Lösung:
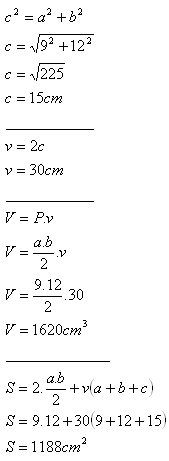
Das Prisma hat das Volumen V = 1620 cm
3 und die Oberfläche S = 1188 cm
2.
12. Wie viel Erde muss bewegt werden, wenn ein gerader Graben von 170 m Länge mit einem gleichschenkligen Trapezquerschnitt (Basen a = 150 cm, c = 80 cm und Höhe v = 83 cm) ausgehoben wird?
Lösung:
l = 170 m = 17000 cm
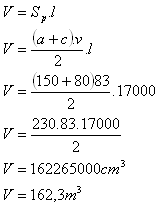
Es müssen etwa 162,3 m
3 Erde bewegt werden.
13. Berechne das Volumen und die Oberfläche eines Prismas, dessen Basis eine Raute mit Diagonalen u1 = 12 cm, u2 = 16 cm ist. Die Höhe des Prismas entspricht dem Doppelten der Basisseite.
Lösung:
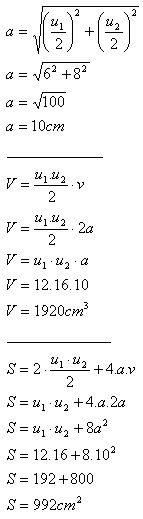
Das Volumen des Prismas beträgt V = 1920 cm
3 und seine Oberfläche S = 992 cm
2.
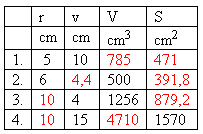
14. Die Tabelle enthält Größen, die verschiedene Zylinder kennzeichnen.
Vervollständige die Tabelle!
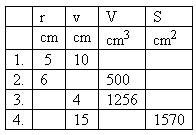
Lösung:
15. Die Mantelfläche eines geraden Kreiszylinders, auf die in der Ebene abgerollt, ein Quadrat mit der Fläche a2 = 81 cm2 ergibt.
Bestimme den Grundradius r, die Höhe v und das Volumen V des Zylinders.
Lösung:
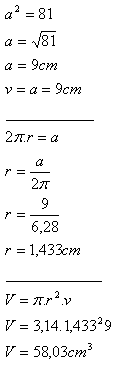
Der Zylinder hat den Grundradius r = 1,433 cm, die Höhe v = 9 cm und das Volumen V = 58,03 cm
3.
16. Ein gleichseitiger Zylinder (v = 2r) hat das Volumen V = 250 cm3.
Berechne die Oberfläche dieses Körpers.
Lösung:
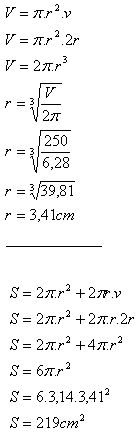
Die Oberfläche dieses Zylinders beträgt S = 219 cm
2.
17. Ein Aluminiumdraht (ρ = 2,7 g·cm-3) mit dem Durchmesser d = 3 mm hat eine Gesamtmasse von m = 1,909 kg.
Bestimme die Länge des Drahts l.
Lösung:
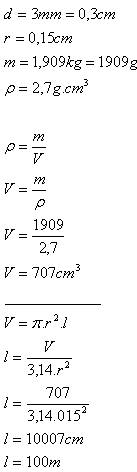
Die Länge des Aluminiumdrahts beträgt ungefähr 100 m.
18. Der äußere Umfang eines Messingrohrs (ρ = 8,5 g·cm-3) beträgt 31,4 cm. Seine Masse ist 3,14 kg und seine Länge 60 cm.
Wie dick ist die Wand des Rohrs?
Lösung:
O = 31,4 cm
v = 60 cm
m = 3140 g
ρ = 8,5 g·cm
-3
Wandstärke = x
In dieser Aufgabe handelt es sich um das Volumen eines hohlen Zylinders mit einem Kreisring als Basis.
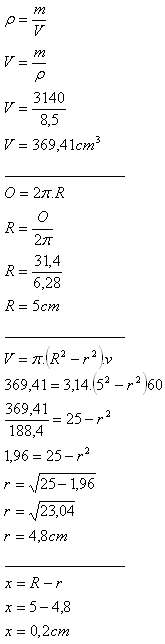
Die Wandstärke des Rohrs beträgt x = 0,2 cm.