Pyramide und Kegel

1. Charakterisiere die Berechnung von Volumen und Oberfläche für:

Pyramide
abgeschnittene Pyramide
Kegel
abgeschnittener Kegel

Lösung:

Pyramide (Sₚ = Grundfläche, v = Höhe, Q = Mantelfläche)

V = \frac{1}{3} S_{p} \cdot v, S = S_{p} + Q

Abgeschnittene Pyramide (Sₚ₁, Sₚ₂ = untere und obere Grundfläche, v = Höhe, Q = Mantelfläche)

V = \frac{1}{3} v (\sqrt{S_{p 1}} + \sqrt{S_{p 2}})^{2}, S = S_{p 1} + S_{p 2} + Q

Kegel (r = Radius der Grundfläche, v = Höhe des Körpers, s = Mantellinie, Q = Mantelfläche)

V = \frac{1}{3} π r^{2} v, S = π r (r + s), Q = π r s

Abgeschnittener Kegel (r₁, r₂ = Radien der Grundflächen, v = Höhe des Körpers, s = Mantellinie)

V = \frac{1}{3} π v (r_{1}^{2} + r_{1} r_{2} + r_{2}^{2}), S = π (r_{1}^{2} + r_{2}^{2}) + Q, Q = π s (r_{1} + r_{2})

2. Eine regelmäßige quadratische Pyramide ist gegeben (die Grundfläche ist ein Quadrat mit der Seite a).

Fülle die fehlenden Werte in der Tabelle aus.

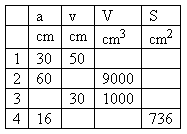
pyramid-cone-2

Lösung:

Für die Seitenhöhe gilt:
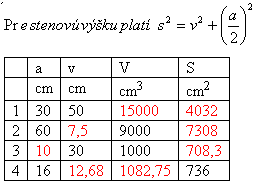
pyramid-cone-2r

3. Über jeder Fläche eines Würfels mit Kantenlänge a = 30 cm wird eine regelmäßige quadratische Pyramide mit der Höhe 15 cm errichtet.

Berechne das Volumen des auf diese Weise gebildeten Körpers, wenn die Spitzen der Pyramiden:
a) außerhalb des Würfels liegen
b) innerhalb des Würfels liegen

Lösung:

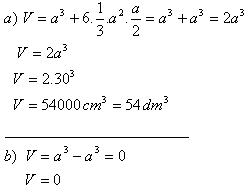
Das Volumen des Körpers beträgt im ersten Fall V = 54 dm³, im zweiten Fall ist es null.

4. Berechne das Volumen einer Pyramide, deren Seitenkante von 5 cm Länge mit der quadratischen Grundfläche einen Winkel α = 60° bildet. (Der Winkel α ist der Winkel zwischen der Kante und der Diagonale der Grundfläche.)

Lösung:

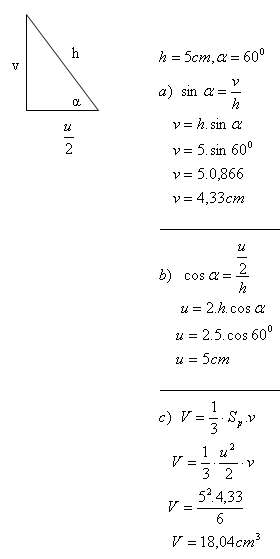
Das Volumen der Pyramide beträgt V = 18,04 cm³.

5. Bestimme die Masse einer Betonsäule (ρ = 2,2 g.cm^-3) in Form eines regelmäßigen quadratischen Pyramidenstumpfes, wenn ihre quadratischen Grundflächen die Seiten a = 45 cm, b = 25 cm und die Höhe v = 33 cm haben.

Lösung:

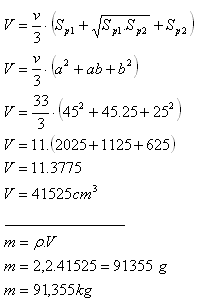
Die Masse der Betonsäule beträgt m = 91,355 kg.

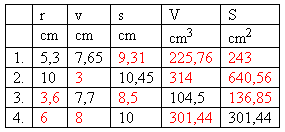
6. Ein Kegel mit in der Tabelle angegebenen Abmessungen ist gegeben.

Fülle die Tabelle aus.

pyramid-cone-6

Lösung:

7. Ein rechtwinkliges Dreieck mit den Katheten a = 3 cm, b = 4 cm rotiert um die längere Kathete.

Berechne das Volumen und die Oberfläche des entstehenden Kegels.

Lösung:

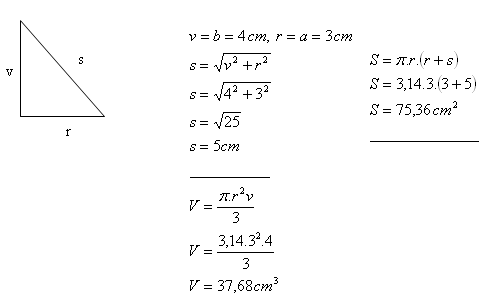
Der Kegel hat das Volumen V = 37,68 cm³ und die Oberfläche S = 75,36 cm².

8. Die Oberfläche eines Kegels beträgt S = 235,5 cm². Der Axialschnitt des Kegels ist ein gleichseitiges Dreieck.

Berechne das Volumen des Kegels.

Lösung:

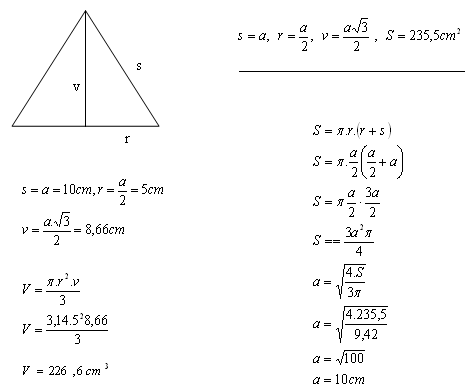
Das Volumen des Kegels beträgt 226,6 cm³.

9. Die Mantelfläche eines Kegels, die in der Ebene ausgebreitet ist, hat die Form eines Kreissektors mit dem Mittelpunktswinkel α = 150° und der Fläche S = 523,4 cm².

Berechne die Abmessungen dieses Kegels und sein Volumen.

Lösung:

S = 523,4 cm² – Fläche des Kreissektors mit Radius R – Mantelfläche mit Radius r
o = R · Bogenα – Kreisbogen, der dem Sektor entspricht
O = 2πr – Umfang der Grundfläche des Kegels

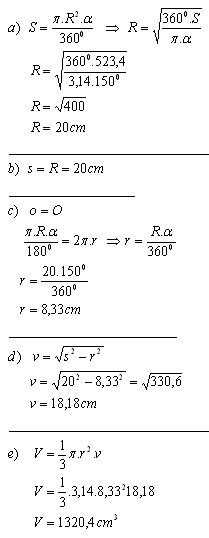
pyramid-cone-9

Die Abmessungen des Kegels sind r = 8,33 cm, s = 20 cm, v = 18,18 cm und das Volumen V = 1320,4 cm³.

10. Die Oberfläche eines abgeschnittenen Kegels beträgt 7693 cm², die Radien der Grundflächen sind 28 cm und 21 cm.

Berechne die Höhe des Kegels und sein Volumen.

Lösung:

S = 7693 cm²
R = 28 cm
r = 21 cm

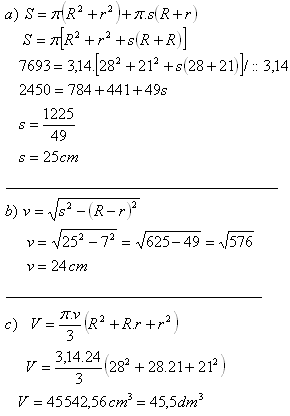
pyramid-cone-10

Die Höhe des Kegels beträgt v = 24 cm, sein Volumen V = 45,5 dm³.

11. Das Volumen eines abgeschnittenen Kegels beträgt V = 38 000π cm³. Der Radius der unteren Grundfläche ist um 10 cm größer als der Radius der oberen Grundfläche.

Bestimme die Radien der Grundflächen, wenn v = 60 cm.

Lösung:

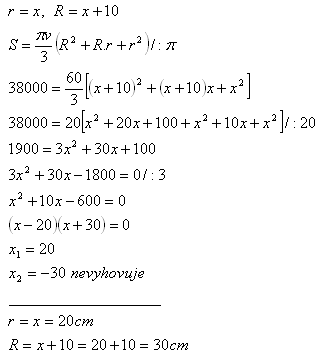
Die Radien der Grundflächen des abgeschnittenen Kegels sind R = 30 cm und r = 20 cm.

12. Ein abgeschnittener Kegel mit den Radien x = 15 cm, y = 13 cm und der Höhe v = 9 cm wurde zu einem Zylinder mit dem Radius r = 7,67 cm aufgerollt.

Wie lang ist dieser Zylinder?

Lösung:

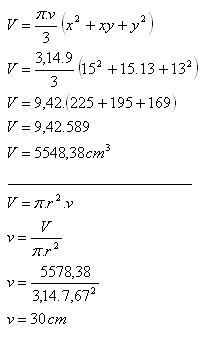
Die Länge / Höhe des Zylinders beträgt 30 cm.

Mathematik

Pyramide und Kegel

Adblock detected