Statistik

1. Erkläre die folgenden Begriffe:

Lösung:

Verteilungskennwerte

a) Arithmetisches Mittel:


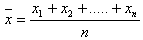
b) Geometrisches Mittel:


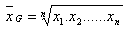
c) Harmonisches Mittel:


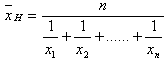
d) Modus mod(x) ist der Wert, der in einer Datenreihe oder Wahrscheinlichkeitsverteilung am häufigsten vorkommt.

e) Median med(x) ist:

• der mittlere Wert einer der Größe nach geordneten Datenreihe mit ungerader Anzahl von Elementen
• das arithmetische Mittel der beiden mittleren Werte einer der Größe nach geordneten Datenreihe mit gerader Anzahl von Elementen

Streuungskennwerte

a) Spannweite  

R = x_max - x_min

b) Varianz (Streuung)


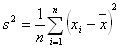
c) Standardabweichung  

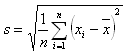
2. Folgende Werte wurden im Labor gemessen (in Millimetern):
{302;310;312;310;313;318;305;309;310;309}

Lösung:

Sortierte Werte:
{302;305;309;309;310;310;310;312;313;318}

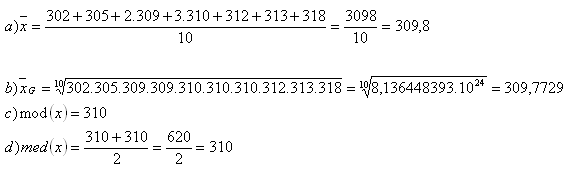
3.Ein Auto fuhr in der ersten Hälfte der Strecke mit einer Durchschnittsgeschwindigkeit von v₁ = 20 km/h und in der zweiten Hälfte mit v₂ = 80 km/h. Bestimme die Durchschnittsgeschwindigkeit des Autos.

Lösung:

Das Auto fuhr mit unterschiedlichen Geschwindigkeiten, daher legte es jede Hälfte der Strecke in unterschiedlicher Zeit zurück.
Die Durchschnittsgeschwindigkeit entspricht dem harmonischen Mittel von v₁ und v₂.



Die Durchschnittsgeschwindigkeit des Autos betrug 32 km/h.

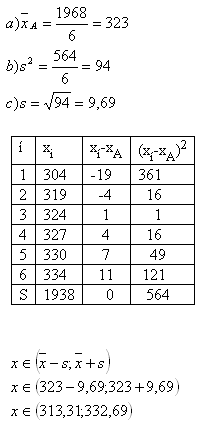
4.Folgende Werte wurden zur Bestimmung des Gewichts eines Zahnrads gemessen. Finde das Intervall, das den tatsächlichen Gewichtswert mit einer Wahrscheinlichkeit von 68 % enthält.

Lösung:

5. Die Schützen A und B treten im Zielschießen gegeneinander an. Wer war präziser und gewann den Wettbewerb?

Lösung:

Schütze A


Schütze B


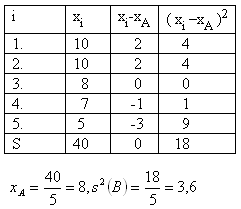
Die Varianz von Schütze A beträgt s²(A) = 0,4, die Varianz von Schütze B beträgt s²(B) = 3,6. Es gilt s²(A) < s²(B).
Schütze A gewann den Wettbewerb.