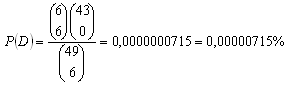Wahrscheinlichkeit
1.Definiere und charakterisiere Wahrscheinlichkeit.
Lösung:
a)
Standarddefinition der Wahrscheinlichkeit
Ein zufälliges Ereignis erfülle die folgenden Bedingungen:
- Die Anzahl der Ereignisse ist endlich
- Alle Ereignisse haben die gleiche Wahrscheinlichkeit, einzutreten
- Keine zwei Ereignisse können gleichzeitig eintreten
Die Wahrscheinlichkeit eines Ereignisses A ist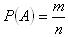 
, n = Anzahl aller möglichen Ereignisse, m = Anzahl der für A günstigen Fälle
Es gilt: 0 ≤ P(A) ≤ 1
Wahrscheinlichkeit eines unmöglichen Ereignisses: P(A) = 0
Wahrscheinlichkeit eines sicheren Ereignisses: P(A) = 1
b) Bedingte Wahrscheinlichkeit eines Ereignisses A unter der Bedingung, dass ein anderes Ereignis B eingetreten ist:
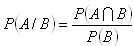
c) Wahrscheinlichkeit zweier unabhängiger Ereignisse:
P(A∩B) = P(A)P(B)
d) Wahrscheinlichkeit zweier sich gegenseitig ausschließender Ereignisse:
P(AUB) = P(A) + P(B)
e) Binomialverteilung der Wahrscheinlichkeit:
Tritt ein Ereignis A mit der Wahrscheinlichkeit P ein, so gilt: Die Wahrscheinlichkeit, dass das Ereignis A in n Versuchen genau k-mal eintritt, ist:
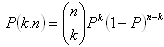
f) Hypergeometrische Wahrscheinlichkeit:
Eine Menge V von N Elementen hat eine Eigenschaft p; folglich haben N-V Elemente die Eigenschaft p nicht.
Die Wahrscheinlichkeit, dass unter n zufällig ausgewählten Elementen k die Eigenschaft p besitzen, ist::
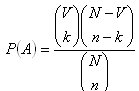
2.Es gibt 18 Lose mit den Nummern 1 bis 18. Wie groß ist die Wahrscheinlichkeit, ein Los mit der folgenden Eigenschaft zu ziehen:
a) gerade Zahl
b) durch 3 teilbare Zahl
c) Primzahl
d) durch 6 teilbare Zahl
Lösung:
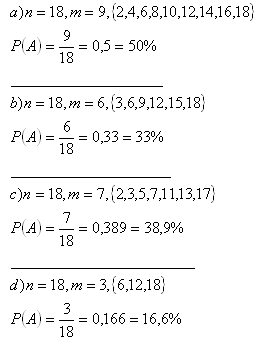
3.Bestimme die Wahrscheinlichkeit folgender Ergebnisse beim Werfen von 2 Spielwürfeln (ein roter und ein blauer):
a) Summe = 8
b) Summe durch 5 teilbar
c) gerade Summe
Lösung:
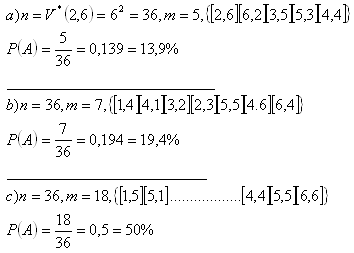
4.Ein Spieler, der mit 3 Würfeln spielt, möchte wissen, ob er auf die Summe 11 oder 12 setzen soll. Welche Summe tritt wahrscheinlicher auf?
Lösung:
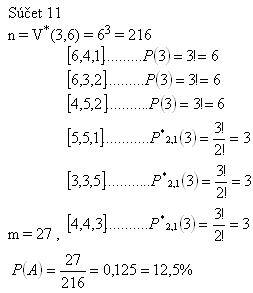
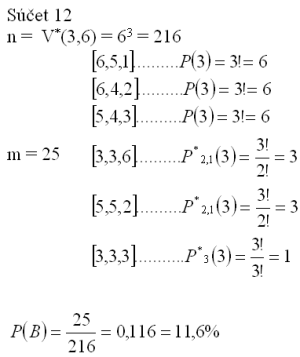
Der Spieler sollte auf 11 setzen, da P(11) > P(12).
5.82 170 von 100 000 Kindern leben 40 Jahre und 37 930 von 100 000 Kindern leben 70 Jahre. Bestimme die Wahrscheinlichkeit, dass eine 40-jährige Person 70 Jahre alt wird.
Lösung:
(Bedingte Wahrscheinlichkeit)
A – lebt 70 Jahre, P(A) = 0,3793
B – lebt 40 Jahre, P(B) = 0,8217
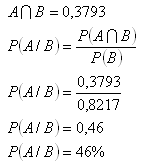
Die Wahrscheinlichkeit beträgt 46%.
6.In einer Stadt gibt es 4 Kreuzungen mit Ampeln. Jede Ampel zeigt mit gleicher Wahrscheinlichkeit Grün oder Rot (0,5). Bestimme die Wahrscheinlichkeit für:
a) ein Auto überquert die erste Kreuzung ohne anzuhalten
b) ein Auto überquert die ersten zwei Kreuzungen ohne anzuhalten
c) ein Auto überquert alle 4 Kreuzungen ohne anzuhalten
Lösung:
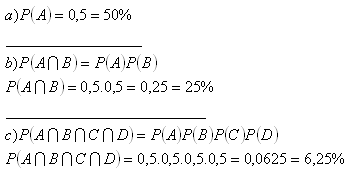
7.Ein Kartenspiel mit 32 Karten enthält 4 Asse und 12 Bildkarten. Bestimme die Wahrscheinlichkeit, dass eine zufällig gezogene Karte ein Ass oder eine Bildkarte ist.
Lösung:
Wahrscheinlichkeit zweier sich gegenseitig ausschließender Ereignisse
A – gezogene Karte ist ein Ass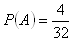 
B - gezogene Karte ist eine Bildkarte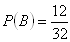 
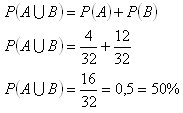
Die Wahrscheinlichkeit, ein Ass oder eine Bildkarte zu ziehen, beträgt 50%.
8.Bestimme die Wahrscheinlichkeit, dass von 5 geborenen Kindern 3 Jungen sind, wenn die Wahrscheinlichkeit, dass ein Kind ein Junge ist, P(A) = 0,51 beträgt.
Lösung:
Binomialverteilung.
n = 5, k = 3, P = 0,51
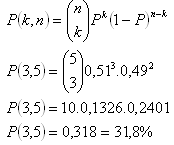
Die Wahrscheinlichkeit beträgt 31,8 %.
9. Auf dem Tisch stehen 16 Colaflaschen. 10 davon sind mit Coca-Cola und 6 mit Pepsi gefüllt. Bestimme die Wahrscheinlichkeit, dass unter 4 zufällig ausgewählten Flaschen 2 Coca-Cola und 2 Pepsi sind.
Lösung:
Hypergeometrische Wahrscheinlichkeit.
N = 16 (Gesamtzahl der Flaschen)
V = 10 (Anzahl Coca-Cola)
N-V = 6 (Anzahl Pepsi)
n = 4 (Anzahl der zufällig ausgewählten Flaschen)
k = 2 (Anzahl ausgewählter Coca-Cola)
n – k = 2 (Anzahl ausgewählter Pepsi)
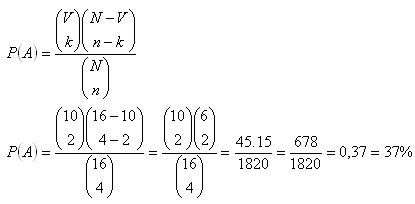
Die Wahrscheinlichkeit beträgt P(A) = 37 %.
10.In einem Glücksspiel sind 6 von 49 Zahlen die Gewinnzahlen. Bestimme die Wahrscheinlichkeit für:
a) 3 von 6 Treffer
b) 4 von 6 Treffer
c) 5 von 6 Treffer
d) 6 von 6 Treffer
Lösung:
a) 3 von 6 Treffer
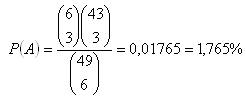
b) 4 von 6 Treffer
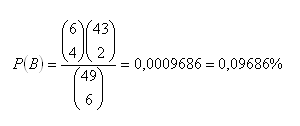
c) 5 von 6 Treffer
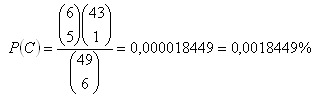
d) 6 von 6 Treffer
