Kirchhoffsche Gesetze

1.Erläutern Sie die Anwendung der Kirchhoffschen Gesetze in der Elektrotechnik.

Lösung:

Die Kirchhoffschen Gesetze werden verwendet, um ein verzweigtes elektrisches Netzwerk zu lösen – also ein elektrisches System, das mehrere Spannungsquellen und Widerstände enthält, die auf verschiedene Weise miteinander verbunden sind. Ein Knoten ist ein Punkt im Stromkreis, an dem sich mindestens drei Leiter treffen. Ein Zweig ist ein Teil des Stromkreises zwischen zwei Knoten.

1. Kirchhoffsches Gesetz:
$I_{1} + I_{2} + \dots + I_{k} = 0$
In einem elektrischen Netzwerk mit stationären Strömen ist die algebraische Summe der Ströme an jedem Knoten gleich null.

2. Kirchhoffsches Gesetz:
$U_{0} + U_{0} + \dots + U_{0 k} = R I_{1} + \dots + R_{k k}$
In einem elektrischen Netzwerk mit stationären Strömen ist die algebraische Summe der von Quellen erzeugten elektromotorischen Spannungen gleich der Summe der Spannungsabfälle über den einzelnen Widerständen.
Vereinfacht:
$I_{1} + I_{2} = I \land R_{1} I_{1} = R I_{2, 2}$

Strommessung:
Wir erweitern den Messbereich eines Amperemeters, indem wir einen Nebenschluss parallel zum Amperemeter anschließen.

R_b = \frac{R A}{n - 1}

Spannungsmessung:
Wir erweitern den Messbereich eines Voltmeters durch einen in Reihe geschalteten Widerstand.

2.Ein Strom von 1,5A teilt sich auf zwei parallel geschaltete Widerstände auf, R₁ = 4Ώ und R₂ = 6Ώ. Wie groß ist der Strom in jedem Widerstand?

Lösung:

Analyse:

I = 1,5A, R₁ = 4Ώ , R₂ = 6Ώ, I₁ = ?, I₂ = ?

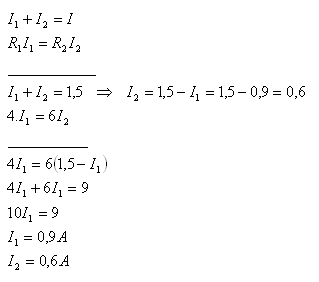
Die Ströme durch die Widerstände sind I₁ = 0,9A und I₂ = 0,6A.

3.Zwei Geräte mit den Widerständen R₁ = 400Ώ und R₂ = 600Ώ sind parallel geschaltet und werden mit einer Spannung von 300V versorgt. Bestimmen Sie die elektrischen Ströme durch die Geräte.

Lösung:

Analyse:

R₁ = 400Ώ, R₂ = 600Ώ, U = 300V, R = ?, I = ?, I₁ = ?, I₂ = ?

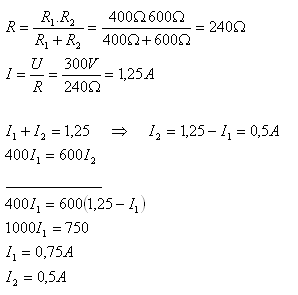
Die Ströme durch die Geräte sind I₁ = 0,75A und I₂ = 0,5A.

4.Ein Amperemeter hat einen Messbereich von 1,2A und einen Widerstand von 0,02Ώ. Wie groß muss der Nebenschlusswiderstand sein, damit Ströme bis 6A gemessen werden können?

Lösung:

Analyse:

I = 1,2A, R_A = 0,02Ώ, I‘ = 6A, R_b = ?

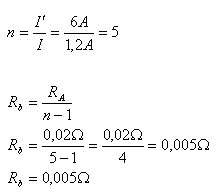
Der Nebenschlusswiderstand muss R_b = 0,005Ώ betragen.

5.Das Voltmeter ist für eine maximale Spannung von 10V ausgelegt, und wir möchten Spannungen bis zu 100V messen. Wie groß ist der Serienwiderstand, wenn R_V = 1kΏ ist?

Lösung:

Analyse:

U‘ = 100V, U = 10V, R_V = 1000Ώ, R_p = ?

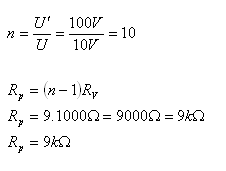
Der Serienwiderstand beträgt R_p = 9kΏ.

Physik

Kirchhoffsche Gesetze

Adblock detected