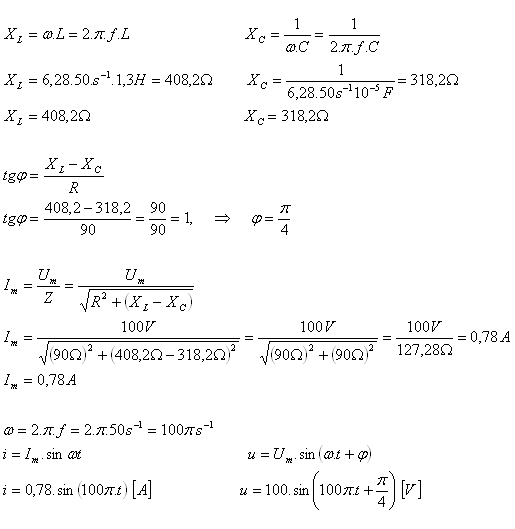Wechselstromkreise

1. Charakterisiere Wechselstrom und Wechselstromschaltungen.

Lösung:

Wechselstrom (AC) ist ein zeitlich veränderlicher, periodisch sich ändernder elektrischer Strom. Sowohl der Betrag als auch die Richtung des Stromes ändern sich. Wechselstrom wird auf Grundlage des Gesetzes der elektromagnetischen Induktion erzeugt: Wenn ein Leiter (eine Spule) sich in einem homogenen Magnetfeld dreht, wird in dem Leiter eine Wechselspannung und ein Wechselstrom induziert.

Wechselstromschaltungen:

1) Schaltung mit Widerstand (Resistor) R

$u = U_{m} \sin ω t, i = I_{m} \cos ω t$

Der momentane Strom und die momentane Spannung sind in Phase.

Ohmscher Blindwiderstand:

X_R = \frac{U_m}{I_m} = R,\quad [X_R] = 1\,\Omega

2) Schaltung mit Induktivität (Spule) L

$u = U_m \sin \omega t,\quad i = I_m \sin(\omega t - \pi/2)$

Der Strom eilt der Spannung nach.

Induktiver Blindwiderstand:

X_L = \frac{U_m}{I_m} = \omega L,\quad [X_L] = 1\,\Omeg

3) Schaltung mit Kapazität (Kondensator) C

$u = U_{m} \sin ω t, i = I_{m} \sin (ω t + π / 2)$

Der Strom eilt der Spannung voraus.

Kapazitiver Blindwiderstand:

X_C = \frac{U_m}{I_m} = \frac{1}{\omega C},\quad [X_C] = 1\,\Omega

4) Reihenschaltungen RLC, RL, RC, LC

Impedanz:

Z = \frac{U_m}{I_m},\quad [Z] = 1\,\Omega

RLC:

Z = \sqrt{R^2 + (X_L - X_C)^2},\quad \tan\varphi = \frac{X_L - X_C}{R}

RL:

Z = \sqrt{R^2 + X_L^2},\quad \tan\varphi = \frac{X_L}{R}

RC:

Z = \sqrt{R^2 + X_C^2},\quad \tan\varphi = -\frac{X_C}{R}

LC:

Z = X_L - X_

Bedingung: Bei Resonanz gilt

Z = 0 \Rightarrow X_L = X_C

2.Eine Wechselspannung mit der Frequenz f = 50 Hz hat die Amplitude U_m = 200 V. Schreibe die Gleichung der Wechselspannung. Bestimme den momentanen Spannungswert zum Zeitpunkt t = 4 ms.

Lösung:

Analyse:

U_m = 200 V, f = 50 Hz, t = 4 ms, u = ?

u = U_m·sin(ωt)
u = U_m·sin(2·π·f·t)
u = 200 V·sin(2·π·50·t)
u = 200·sin(100·π·t)

u = 200 V·sin(100·π·50·s^-1·4·10^-3s) = 200 V·sin(72°)
u = 200 V·0.951 = 190.2 V
u = 190.2 V

Die Gleichung der Wechselspannung lautet u = 200·sin(100·π·t).
Der momentane Spannungswert zum Zeitpunkt t = 4 ms ist u = 190.2 V.

3.Der Wechselstrom in einem elektrischen Stromkreis wird durch die Gleichung i = 5·sin(200·π·t) [A] beschrieben. Bestimme die Stromamplitude, die Frequenz und die Periodendauer des Stromes. Bestimme außerdem den momentanen Stromwert zum Zeitpunkt t = 1.25·10^–3 s.

Lösung:

i = 5·sin(200·π·t) [A]
i = I_m·sin(ω·t)

I_m = 5 A,

ω·t = 200·π·t,    2·π·f = 200·π,   2·f = 200 s^-1, f = 100 Hz

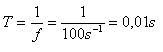
i = 5·sin(200·π·t) [A]
i = 5·sin(200·π·1.25·10^-3 s) [A]
i = 5·sin(45°) = 5·0.707 A = 3.54 A
i = 3.54 A

I_m = 5 A,   f = 100 Hz, T = 0.01 s, i = 3.54 A.

4.Bestimme den Blindwiderstand einer Spule mit Induktivität 500 mH in einem Wechselstromkreis mit der Frequenz 50 Hz. Berechne die Stromamplitude, wenn die Spannungsamplitude 314 V beträgt.

Lösung:

Analyse:

L = 500·10^-3 H, f = 50 s^-1, U_m = 314 V, X_L = ?, I_m = ?

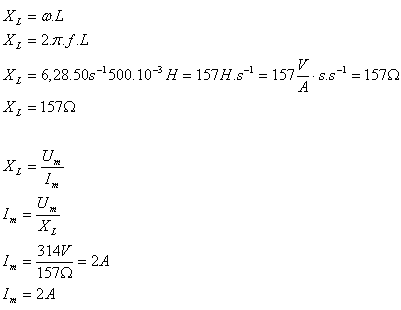
Der induktive Blindwiderstand der Spule beträgt X_L = 157 Ω, die Stromamplitude beträgt I_m = 2 A.

5. Bestimme den Blindwiderstand eines Kondensators mit Kapazität 20 μF in einem Wechselstromkreis mit der Frequenz 50 Hz. Berechne außerdem die Spannungsamplitude, wenn die Stromamplitude 2 A beträgt.

Lösung:

Analyse:

C = 20 μF = 20·10^-6 F, f = 50 s^-1, I_m = 2 A, X_C = ?, U_m = ?

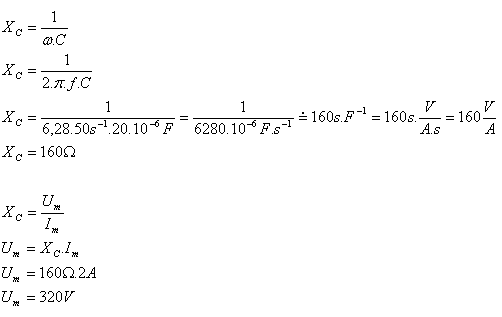
Der kapazitive Blindwiderstand beträgt X_C = 160 Ω, die Spannungsamplitude beträgt U_m = 320 V.

6.Eine Spule mit Induktivität 2 H und Wicklungswiderstand 20 Ω wird zunächst an eine Gleichspannungsquelle mit U = 20 V und anschließend an eine Wechselspannungsquelle mit demselben Effektivwert und der Frequenz 50 Hz angeschlossen. Bestimme den Strom im Stromkreis in beiden Fällen.

Lösung:

Analyse:

L = 2 H, R = 20 Ω, U = 20 V, f = 50 s^-1, I₁ = ?, I₂ = ?

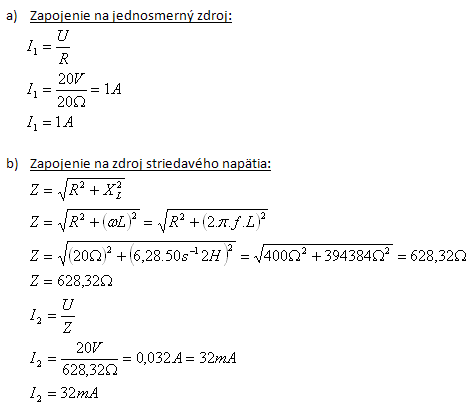
a) Beim Anschluss der Spule an die Gleichspannungsquelle fließt durch sie der Strom I₁ = 1 A,
b) beim Anschluss an die Wechselspannungsquelle fließt der Strom I₂ = 32 mA.

7. Ein Wechselstromkreis mit Effektivspannung 200 V und Frequenz 50 Hz ist an eine Serienschaltung aus einem Kondensator mit Kapazität 16 μF und einem Widerstand mit R = 150 Ω angeschlossen. Bestimme die Impedanz des Stromkreises, den Strom im Stromkreis sowie die Spannungen am Kondensator und am Widerstand.

Lösung:

Analyse:

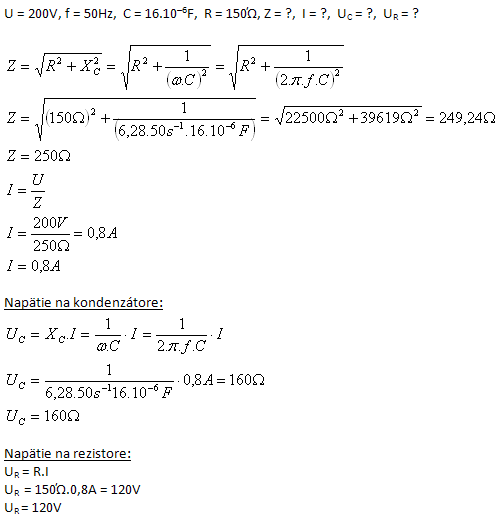
Spannung am Kondensator
Spannung am Widerstand

Die Impedanz des Stromkreises beträgt Z = 250 Ω, der Strom im Stromkreis ist I = 0.8 A, die Spannung am Kondensator ist U_C = 160 V und am Widerstand U_R = 120 V.

8.Ein Schwingkreis besteht aus einer Spule mit Induktivität 0.1 mH und einem Kondensator mit Kapazität 100 pF. Bestimme die Resonanzfrequenz.

Lösung:

Analyse:

L = 0.1 mH = 10^-4 H, C = 10^-10 F, f = ?

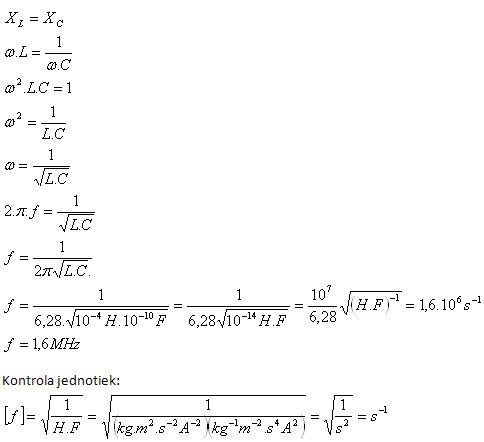
Die Resonanzfrequenz beträgt f = 1.6 MHz.

9.Eine Spule mit L = 5·10^–2 H und Wicklungswiderstand R = 10 Ω ist in Reihe mit einem Kondensator C = 2·10^–6 F geschaltet. In dem Stromkreis fließt ein Wechselstrom mit Amplitude I_m = 0.1 A und f = 500 Hz. Bestimme die Impedanz Z des Stromkreises und die Spannungsamplitude U_m.

Lösung:

Analyse:

L = 5·10^-2 H, R = 10 Ω, C = 2·10^-6 F, I_m = 0.1 A f = 500 Hz, Z = ?, U_m = ?

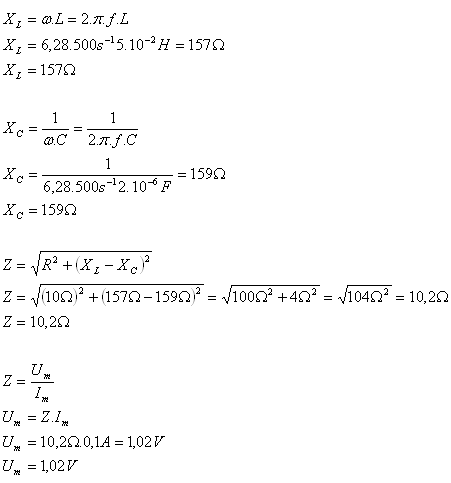
Die Impedanz des Stromkreises beträgt Z = 10.2 Ω, die Spannungsamplitude beträgt U_m = 1.02 V.

10. Ein Serienwechselstromkreis besteht aus einem Widerstand mit R = 90 Ω, einer Spule mit Induktivität L = 1.3 H und einem Kondensator mit Kapazität C = 10^–5 F. Der Stromkreis ist an eine Wechselspannungsquelle mit Amplitude U_m = 100 V und Frequenz f = 50 Hz angeschlossen. Schreibe die Gleichungen für die momentanen Werte von Spannung und Strom im Stromkreis.

Lösung:

Analyse:

R = 90 Ω, L = 1.3 H, C = 10^-5 F, U_m = 100 V, f = 50 Hz

Physik

Wechselstromkreise

RLC:

RL:

RC:

LC:

Adblock detected