Punkt, Gerade und Ebene

1. Erläutere, in welchen gegenseitigen Lagen Folgendes sein kann:

a) ein Punkt und eine Ebene

b) eine Gerade und eine Ebene

Lösung:

Punkt und Ebene.

Der Punkt A[a1; a2; a3] liegt in der Ebene ρ: a.x + by + cz + d = 0, wenn seine Koordinaten die Gleichung der Ebene ρ erfüllen.

Der Punkt A[a1; a2; a3] liegt nicht in der Ebene ρ: ax + by + cz + d = 0, wenn seine Koordinaten die Gleichung der Ebene ρ nicht erfüllen.

Der Abstand des Punktes A[a1; a2; a3] von der Ebene ρ: ax + by + cz + d = 0 ist gegeben durch:

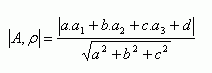
bod-priamka-rovina/bod-priamka-rovina-1

Gerade und Ebene.

Sei $\vec{u} = (u_1, u_2, u_3)$ der Richtungsvektor einer Geraden und $\vec{n} = (a, b, c)$ der Normalenvektor einer Ebene. Dann gilt:

Wenn $\vec{u} \cdot \vec{n} \neq 0$ , schneidet die Gerade die Ebene — sie sind nicht parallel, und ihr Schnittpunkt ist
$p \cap \rho = \{P\}$ .
Wenn $\vec{u} \cdot \vec{n} = 0$ , ist die Gerade parallel zur Ebene — entweder ist $p \cap \rho = \varnothing$ , oder die Gerade liegt in der Ebene, $p \cap \rho = \{P\}$ .

Der Neigungswinkel $\alpha$ der Geraden gegenüber der Ebene ist gegeben durch:

\sin \alpha = \frac{ |\,u_1 n_1 + u_2 n_2 + u_3 n_3\,| }{ |\vec{u}|\,|\vec{n}| }

2. Welche der Punkte A [3;2;7], B[0;2;1], C[-8;-2;-1] liegen in der Ebene τ : 2x – 3y – 2z + 8 = 0? Welchen Wert muss x haben, damit der Punkt M[x;-6;2] ebenfalls in der gegebenen Ebene liegt?

Lösung:

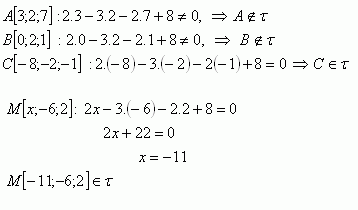
bod-priamka-rovina-2

Die Punkte C [-8;-2;-1] und M [-11;-6;2] liegen in der Ebene τ.

3. Bestimme, ob der Punkt A[9;-2;0] in der Ebene ξ: 3x + 2y – 6z + 26 = 0 liegt. Falls er nicht darauf liegt, berechne seinen Abstand von der gegebenen Ebene.

Lösung:

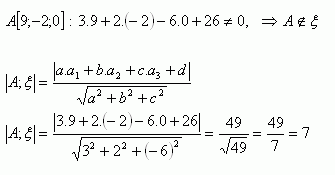
bod-priamka-rovina-3

Der Punkt A liegt nicht in der Ebene ξ. Sein Abstand von dieser Ebene beträgt 7 Einheiten.

4. Berechne den Abstand des Ursprungs des Koordinatensystems von der Ebene:

Lösung:

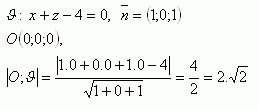
bod-priamka-rovina-4r

Der Abstand des Ursprungs des Koordinatensystems von der Ebene υ beträgt ungefähr 2,828 Einheiten.

5. Bestimme die gegenseitige Lage der Ebenen ρ und τ. Falls sie parallel und verschieden sind, bestimme außerdem ihren Abstand. Die Gleichungen der Ebenen lauten:

Lösung:

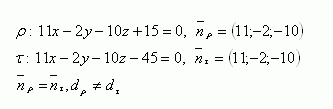
bod-priamka-rovina-5r1

Die Ebenen ρ und τ sind parallel, aber verschieden.

Bestimmung des Abstands zwischen den Ebenen.

In der Ebene ρ suchen wir einen beliebigen Punkt A und bestimmen seinen Abstand von der Ebene τ. Punkt A: wähle x = 1, z = 0, 11.1 - 2y - z.0 + 15 = 0 , 2y = 26, y = 13 → A[1; 13; 0]:

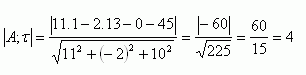
bod-priamka-rovina-5r2

Die Ebenen sind parallel, aber verschieden. Ihr gegenseitiger Abstand beträgt 4 Einheiten.

6. Was muss für die y-Koordinate des Punktes A [1;y;0] gelten, damit sein Abstand von der Ebene τ: 3x – 2y – 6z = 0 gleich 5 Einheiten ist?

Lösung:

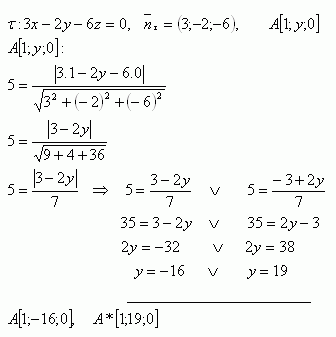
bod-priamka-rovina-6

Die Punkte, die die Bedingungen erfüllen, sind A[1;-16;0] und A*[1;19;0]

7. Bestimme die gegenseitige Lage und den Schnittpunkt der Geraden und der Ebene, falls sie nicht parallel sind.

Ebene:

τ: x + y + z + 1

Gerade:

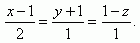
bod-priamka-rovina-7z

Lösung:

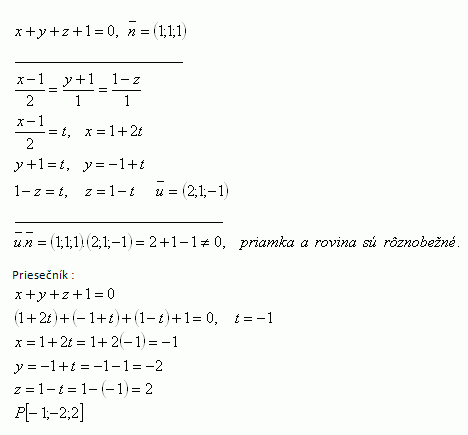
bod-priamka-rovina-7r

Die Gerade schneidet die Ebene im Punkt P [-1; -2; 2].

8. Gegeben sind eine Gerade p und eine Ebene ρ. Bestimme ihren gemeinsamen Punkt und den Winkel zwischen der Geraden und der Ebene. Ihre Gleichungen lauten:

Lösung:

Schnitt der Geraden mit der Ebene: Winkel zwischen der Geraden und der Ebene:

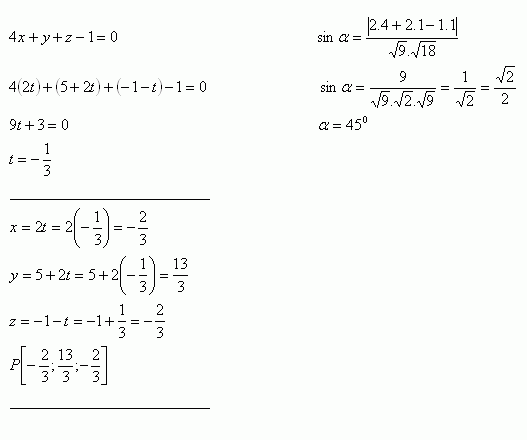
bod-priamka-rovina-8r

9. Bestimme die gegenseitige Lage der Ebenen ρ und π, deren Gleichungen sind:

Lösung:

bod-priamka-rovina-9r

10. Berechne den Winkel zwischen zwei nicht parallelen Ebenen:

Lösung:

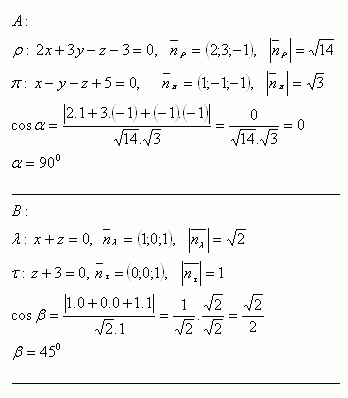
bod-priamka-rovina-10r

11. Bestimme den gemeinsamen Punkt der Geraden p und der Ebene τ, falls gilt:

Lösung:

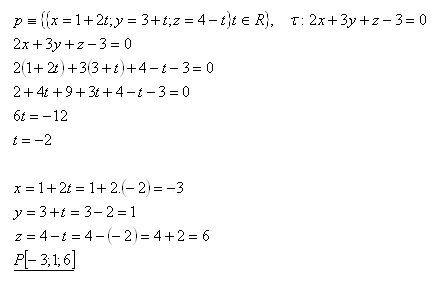
bod-priamka-rovina-11r

Der gemeinsame Punkt der Geraden p und der Ebene τ ist P[-3; 1; 6].

12. Der Abstand des Punktes A von der Ebene σ stellt die Seitenlänge des Quadrats ABCD dar. Berechne den Flächeninhalt dieses Quadrats, falls gilt:

Lösung:

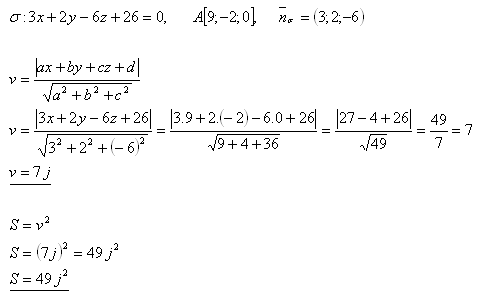
bod-priamka-rovina-12r

Der Flächeninhalt des Quadrats ABCD ist S = 49 j².

13. Berechne den Abstand zweier paralleler Ebenen σ und τ, falls gilt:

Lösung:

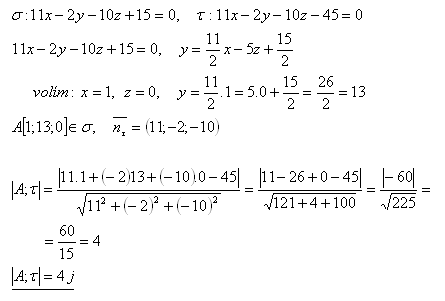
bod-priamka-rovina-13r

Der Abstand der beiden parallelen Ebenen σ und τ beträgt 4 j.

14. Berechne die Länge der Höhe, die vom Scheitelpunkt V im Tetraeder ABCV gefällt ist, falls gilt:

Lösung:

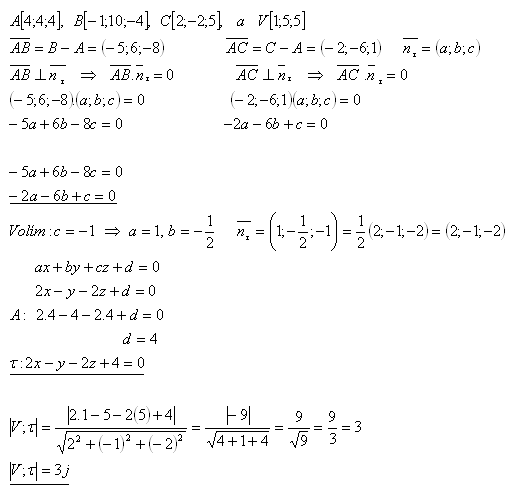
bod-priamka-rovina-14r

Die Höhe des Tetraeders ABCV beträgt 3 Einheiten.

15. Bestimme die reellen Zahlen a, b so, dass die Ebenen π und τ parallel sind, wenn gilt:

Lösung:

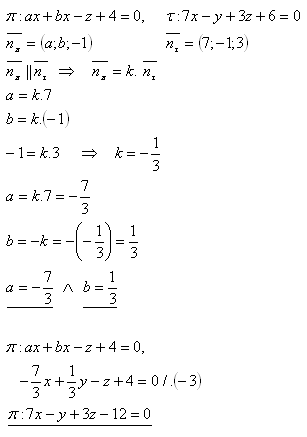
bod-priamka-rovina-15r

16. Bestimme die gegenseitige Lage der Ebenen σ und η, falls gilt:

Lösung:

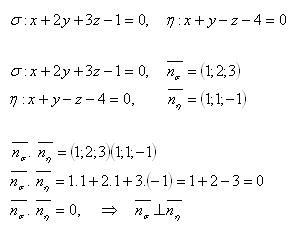
bod-priamka-rovina-16r

Die Ebenen σ und η stehen senkrecht aufeinander.

17. Zeige, dass die Koordinatenebenen xy und yz senkrecht aufeinander stehen.

Lösung:

Koordinatenebene xy = ρ

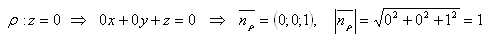
bod-priamka-rovina-17z1

Koordinatenebene yz = λ

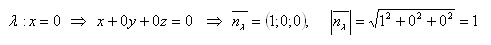
bod-priamka-rovina-17z2

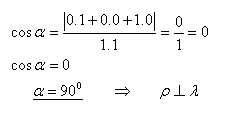
bod-priamka-rovina-17r

Die Koordinatenebenen xy und yz stehen senkrecht aufeinander.

18. Bestimme den Winkel zwischen der Geraden p und der Ebene μ, falls gilt:

Lösung:

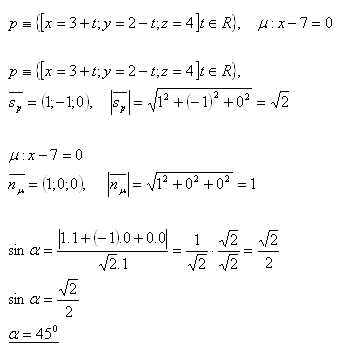
bod-priamka-rovina-18r

Der Winkel zwischen der Geraden p und der Ebene μ ist α = 45⁰.

19. Die Eckpunkte des Tetraeders sind die Punkte A, B, C, D. Bestimme den Winkel zwischen der Kante AD und der Ebene ρ = ABC, falls gilt:

Lösung:

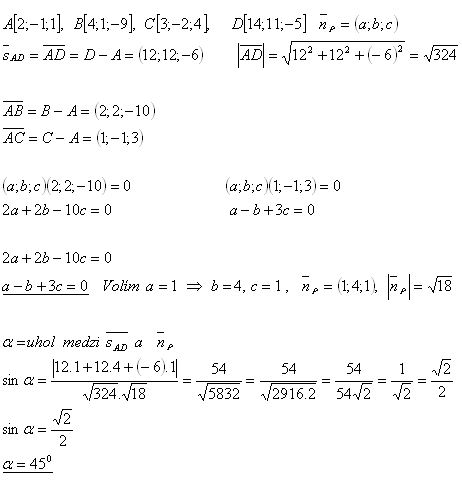
bod-priamka-rovina-19r

Der Winkel zwischen der Kante AD und der Ebene ρ ist α = 45⁰.

20. Bestimme die gegenseitige Lage der drei Ebenen, falls gilt:

Lösung:

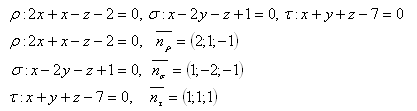
bod-priamka-rovina-20r1

Die Normalenvektoren der gegebenen Ebenen sind unabhängig. Die Ebenen sind nicht parallel.

Schnittpunkt der Ebenen P [x; y; z]:

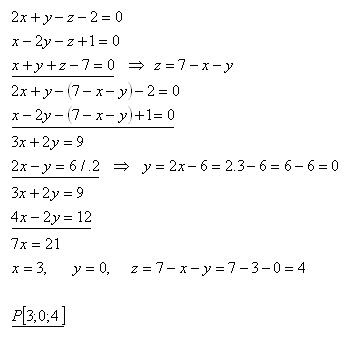
bod-priamka-rovina-20r2

Die Ebenen ρ, σ, τ sind nicht parallel. Sie schneiden sich im Punkt P[3; 0; 4].

Mathematik

Punkt, Gerade und Ebene

Adblock detected