Kegelschnitte
1. Was weißt du über Kegelschnitte:
Lösung:
Kreis ist die Menge aller Punkte in der Ebene, die vom festen Punkt S in der Ebene den gleichen Abstand r haben. S[m ; n] ist der Mittelpunkt und r ist der Radius des Kreises.
Ellipse ist die Menge aller Punkte in der Ebene, für die die Summe der Abstände von den Punkten F1, F2 der Ebene gleich 2a ist. Die Punkte F1[-e;0], F2[e;0] sind die Brennpunkte, Exzentrizität e2 = a2 - b2, a – große Halbachse, b – kleine Halbachse.
Hyperbel ist die Menge aller Punkte in der Ebene, für die der Betrag der Differenz der Abstände von den Punkten F1, F2 der Ebene gleich 2a ist. Die Punkte F1[-e;0], F2[e;0] sind die Brennpunkte, Exzentrizität e2 = a2 + b2. a – reelle, b – imaginäre Halbachse. Gleichungen der Asymptoten der Hyperbel: ( o || x ) : 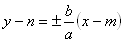
Parabel ist die Menge aller Punkte in der Ebene, deren Abstand von einem Punkt F in der Ebene und von einer in der Ebene liegenden Geraden d gleich ist. Punkt F heißt Brennpunkt der Parabel, d – die Leitgerade. Der Punkt F liegt nicht auf d. Der Wert p ist der Parameter der Parabel.
Die Lage eines Kegelschnitts und einer Geraden bestimmen wir durch Lösen des Gleichungssystems, was auf eine quadratische Gleichung führt. Ist D > 0, so ist die Gerade eine Sekante; ist D = 0, eine Tangente; ist D < 0, so schneidet die Gerade nicht.
| Kurve |
Gleichung S[m;n] |
Zentralform S[0;0] |
Allgemeine Form |
| Kreis |
(x − m)² + (y − n)² = r² |
x² + y² = r² |
x² + y² + Ax + By + C = 0 |
| Ellipse |
((x − m)² / a²) + ((y − n)² / b²) = 1 |
(x² / a²) + (y² / b²) = 1 |
Ax² + By² + Cx + Dy + E = 0, A·B > 0 |
| Hyperbel (o ∥ x) |
((x − m)² / a²) − ((y − n)² / b²) = 1 |
(x² / a²) − (y² / b²) = 1 |
Ax² + By² + Cx + Dy + E = 0, A·B < 0 |
| Parabel (o ∥ y) |
(x − m)² = 2p(y − n) |
x² = 2py |
x² + Ax + By + C = 0 |
| Parabel (o ∥ x) |
(y − n)² = 2p(x − m) |
y² = 2px |
x² + Ax + By + C = 0 |
2.Gib die Gleichung eines Kreises an, der den Radius r = 8 hat und beide Koordinatenachsen berührt.
Lösung:
S [8; 8], r = 8
Die Gleichung des Kreises lautet
3.Bestimme die Gleichung des Kreises, dessen Durchmesser die Strecke AB ist, gegeben A [-1 ; 4 ], B [ 5 ; 6 ].
Lösung:
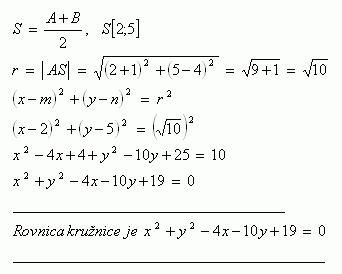
Die Gleichung des Kreises ist
4.Zeige, dass die Gleichungen k: x2 + y2 + 2x + 4y + 1 = 0 und k2: x2 + y2 - 8x + 6y + 9 = 0 Kreise darstellen. Bestimme die Gleichung der Geraden, die durch die Mittelpunkte dieser Kreise verläuft.
Lösung:
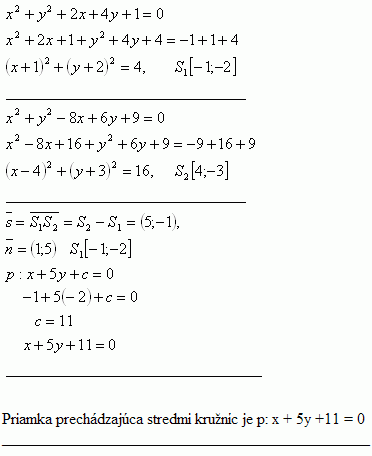
Die durch die Mittelpunkte der Kreise verlaufende Gerade ist
5.Es gibt einen Kreis durch den Punkt A [4; 2], der die Koordinatenachsen berührt. Gib die Gleichung dieses Kreises an.
Lösung:
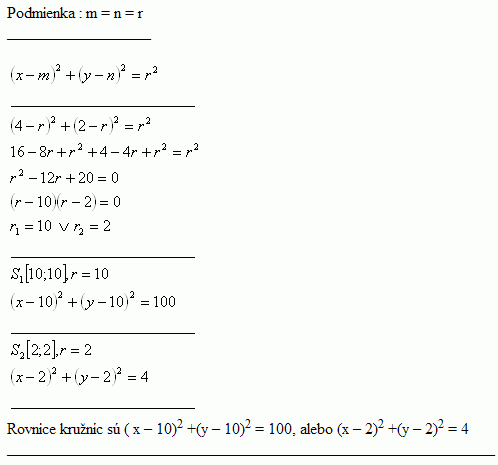
Die Gleichungen der Kreise lauten
6.Der Punkt A [-4 ; 5] ist ein Eckpunkt eines Quadrats, dessen Diagonale auf der Geraden p : [ 7x – y + 8 = 0 ] liegt. Bestimme die Gleichung des Umkreises des Quadrats.
Lösung:
a) Umkreis eines Quadrats:
Die Gleichung des Kreises lautet:
7.Bestimme die Gleichung des Kreises, dessen Mittelpunkt S auf der Geraden p :[ x – y – 1 = 0 ] liegt und der außerdem durch die Punkte A [ -1; -1 ] und B [ 0; 6 ] geht.
Lösung:
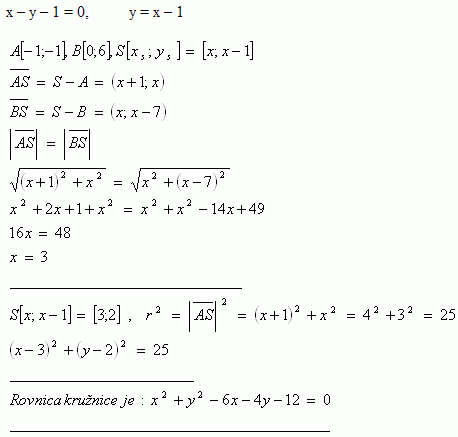
Die Gleichung des Kreises ist
8.Bestimme die Gleichung des Kreises, der durch die Punkte K [2;-1], L [5;-2], M [10;3] geht.
Lösung:
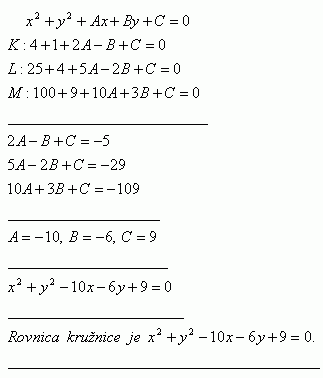
Die Gleichung des Kreises lautet
9.Untersuche die Lagebeziehung der Geraden p: [2x – y – 6 = 0] und des Kreises k: [x2 + y2 – 4x -5y -1 = 0]
Lösung:

Die Gerade ist eine Sekante des Kreises und schneidet ihn in den Punkten
10.Bestimme die Gleichung des Kreises, der zum Kreis k1: ( x – 1 )2 + ( y – 2 )2 = 1 bezüglich der Geraden p: x – y – 3 = 0 symmetrisch ist.
Lösung:
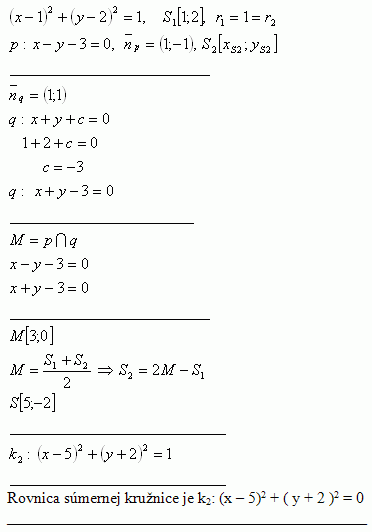
Die Gleichung des Kreises lautet
11.Zwei Eckpunkte einer Raute liegen in den Brennpunkten der Ellipse 9x2 + 25y2 - 225 = 0, die anderen beiden an den Ellipsenendpunkten auf ihrer Nebenachse. Berechne den Flächeninhalt der Raute.
Lösung:
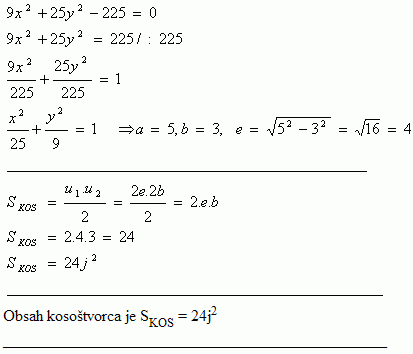
Flächeninhalt der Raute
12.Bestimme die Gleichung der Ellipse in Zentralform mit S [0;0], die durch die Punkte A [8;3] und [6;4] geht.
Lösung:
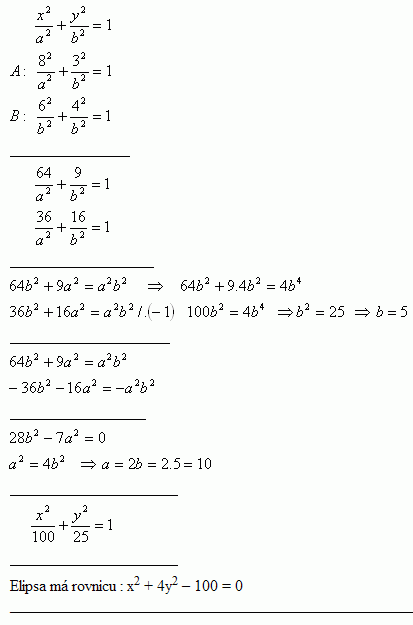
Die Ellipse hat die Gleichung
13.Gib die Gleichung der Geraden an, die durch den Punkt A [1;5] und den Mittelpunkt der Ellipse 4x2 + 9y2 - 24x + 36y +36 = 0 verläuft.
Lösung:
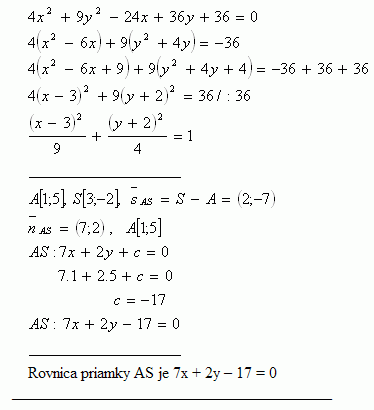
Gleichung einer Geraden
14.In die Ellipse 2x2 + y2 – 4x + 4y – 108 = 0 ist ein Quadrat ABCD eingeschrieben. Finde seinen Umfang und seine Fläche.
Lösung:
2x2 + y2 – 4x + 4y – 108 = 0
(2x2-4x) + (y2+4y) = 108
2(x2-2x+1) +(y2+4y+4) = 108+2+4
2(x-1)2 + ( y+2)2 =114 y = x
2(x2- 2x+1 ) + ( x2 +4x +4 ) = 114
3x2 – 108 = 0
3x2 = 108
x2 = 36
x = ±6
X = (1+x ; -2+x )
A [7; 4 ] B [-5; 4] C [ -5; -8] D [ 7 ; -8]
a = | AB| = |BC| = |CD| = |DA| = 12
a = 12 j
P = 4a , S = a2
P = 4·12 S = 122
P = 48 j S = 144 j2
Der Umfang des Quadrats beträgt P = 48 j, seine Fläche S = 144 j2.
15.Finde den Abstand vom Mittelpunkt der Ellipse 4x2 + 9y2 -16x + 36y + 16 = 0 zur Geraden 5x - 12y + 5 = 0
Lösung:
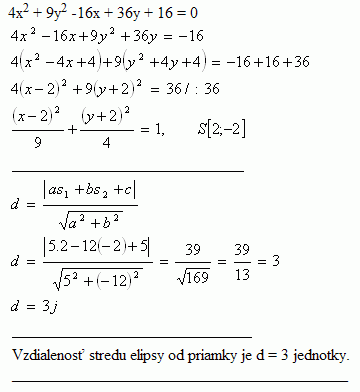
Der Abstand zwischen dem Mittelpunkt der Ellipse und der Geraden beträgt d = 3 Einheiten.
16.Auf einer Ellipse mit Mittelpunkt S [3; 2], Halbachse b = 4, Exzentrizität e = 3 finde den Punkt mit y-Koordinate y = 2.
Lösung:
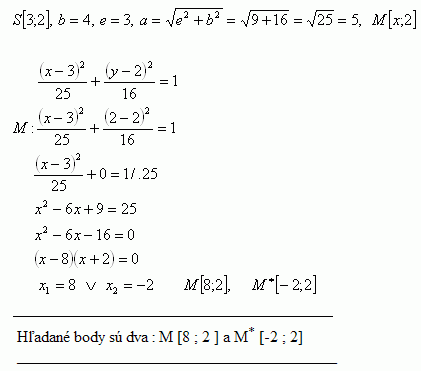
Es sind zwei Punkte zu bestimmen
17.Gegeben ist das Dreieck ΔABC mit Seitenlängen |AB| = 6, |AC| = 7, |BC| = 3. Bestimme die Gleichung der Ellipse, deren Brennpunkte in zwei Eckpunkten des Dreiecks liegen und die durch den dritten Eckpunkt geht.
Lösung:

Die Ellipse hat die Gleichung
18.Bestimme und untersuche den Kegelschnitt, der durch die Punkte geht: K[0;0], L[8;0], M[0;6], N[8;6]. O[2;-2]
Lösung:
Ax2 + By2 + Cx + Dy + E = 0
Löse das Gleichungssystem:
K: 0 + 0 + 0 + E = 0
L: 64A + 0 + 8C + 0 + E = 0
M: 0 + 36B + 0 + 6D + E = 0
N: 64A + 36B + 8C + 6D + E = 0
O: 4A + 4B + 2C – 2D + E = 0
A = 4, B = 3, C = -32, D = -18, E = 0
4x2 + 3y2 – 32x -18y = 0 .
Der Kegelschnitt ist eine Ellipse mit der Gleichung 4x2 + 3y2 -32x -18y = 0
19.Berechne die Länge der Sehne, die die Gerade 2x + y – 14 = 0 aus der Ellipse 4x2 + y2 -100 = 0 ausschneidet.
Lösung:
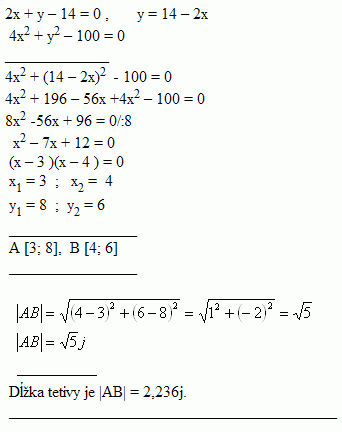
Die Länge der Sehne ist
20.Gib die Gleichung einer Ellipse an, wenn der gegebene Punkt M [3;-1] Endpunkt der kleinen Halbachse b ist und die Brennpunkte auf der Geraden p: y + 6 = 0 liegen. Für die Exzentrizität der Ellipse gilt:
Lösung:
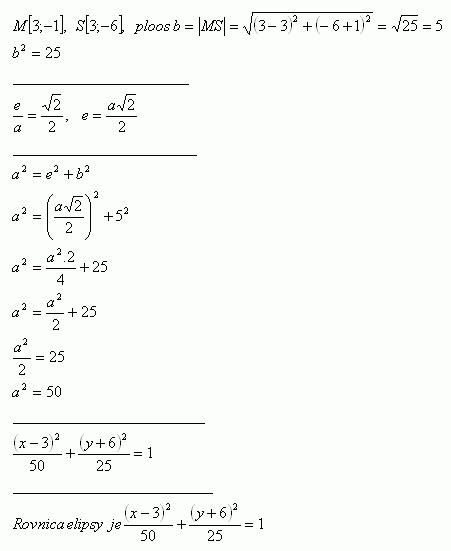
Die Ellipse hat die Gleichung
21.Bestimme den Mittelpunkt und die Halbachsen der Hyperbel 9x2 -16y2 -36x + 32y – 124 = 0. Bestimme außerdem die Gleichungen ihrer Asymptoten.
Lösung:
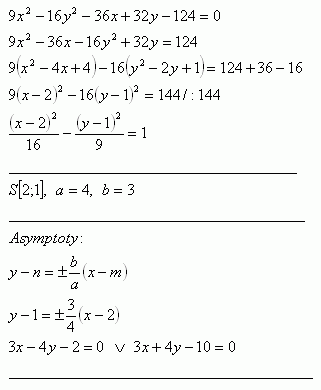
22.Bestimme die Gleichung der Hyperbel, wenn ihre Brennpunkte F1 [-10;2], F2 [16;2] sind. Reelle Achse 2a = 24
Lösung:
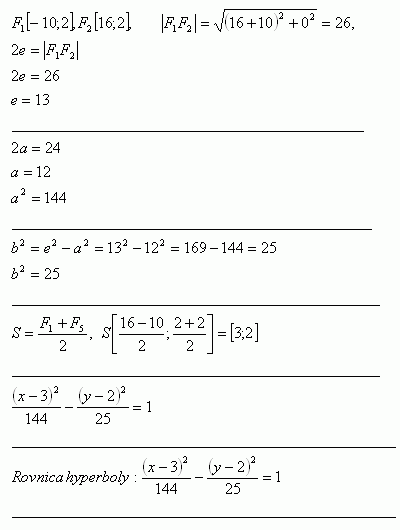
Die Hyperbel hat die Gleichung
23.Bestimme die Gleichung der Geraden, auf der die Symmetrieachse des Segments liegt, das die Mittelpunkte der Hyperbeln x2 – y2 + 6x - 8y – 107 = 0 und 16x2 -9y2 -160x + 36y +220 = 0 verbindet.
Lösung:
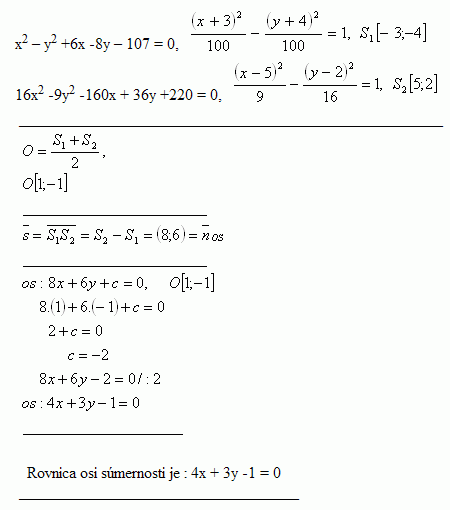
Gleichung der Symmetrieachse
24.Gegeben ist die Hyperbel 16x2 – 25y2 – 400 = 0. Bestimme: a) die Gleichungen der Asymptoten, b) den Winkel zwischen den Asymptoten
Lösung:
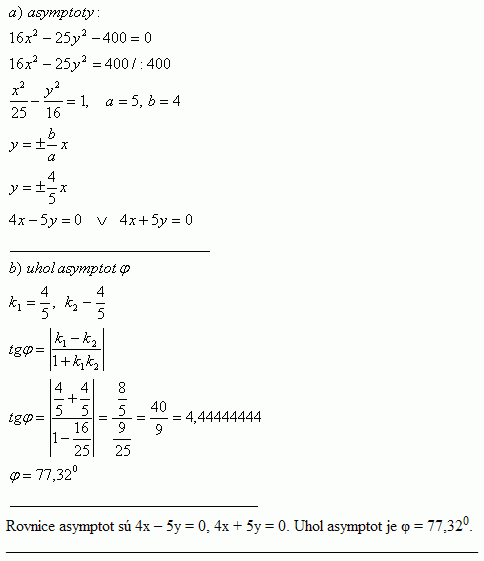
Gleichungen der Asymptoten und Winkel zwischen den Asymptoten
25.Schreibe die Zentralgleichung der Hyperbel, die durch die Punkte geht:
Lösung:
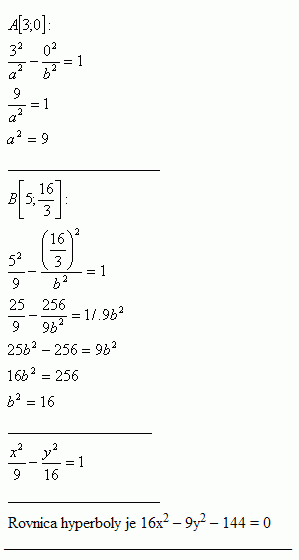
Die Gleichung der Hyperbel lautet
26.Beweise, dass das Produkt der Abstände eines beliebigen Punktes M der Hyperbel 2x2 – y2 – 2 = 0 von ihren Asymptoten konstant ist und gleich 2 : 3.
Lösung:

Die Behauptung ist bewiesen
27.Finde die Menge aller Punkte in der Ebene, deren Verhältnis der Abstände zum Punkt M [-5;0] und zur Geraden p: 5x + 16 = 0 konstant 5 : 4 ist.
Lösung:
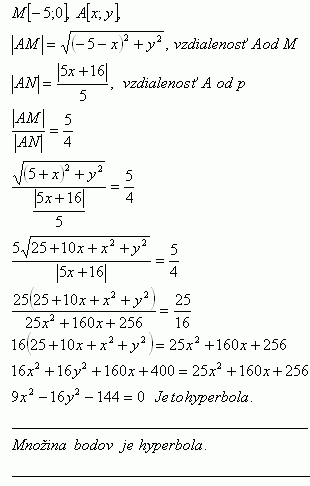
Die Punktmenge ist eine Hyperbel
28.Schreibe die Gleichung der Hyperbel, deren Scheitel in den Brennpunkten der Ellipse x2 + 2y2 – 18 = 0 liegen und deren Brennpunkte in den Scheiteln dieser Ellipse.
Lösung:
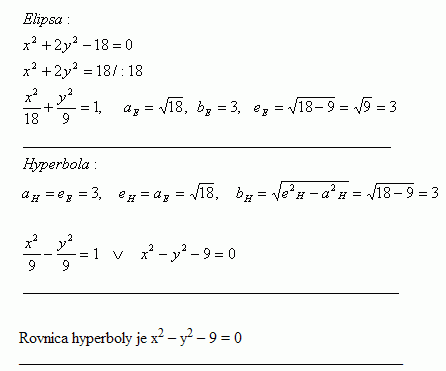
Gleichung der Hyperbel
29.Schreibe die Gleichung der Geraden, die durch den Punkt M [5 ; 4] und den Scheitel V der Parabel y2 - 6x + 10y + 31 = 0 verläuft.
Lösung:
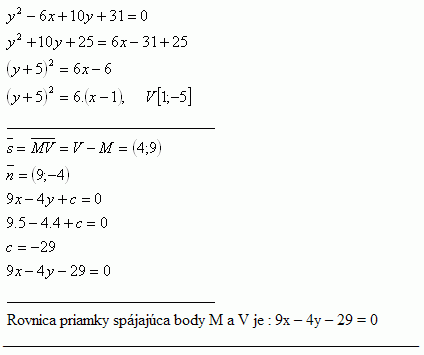
Gleichung der Verbindungsgeraden
30.Gegeben sind die Parabeln x2 - 8x - 3y + 10 = 0 und x2 + 14x - 4y + 61 = 0. Berechne den Abstand ihrer Scheitel |V1V2|
Lösung:
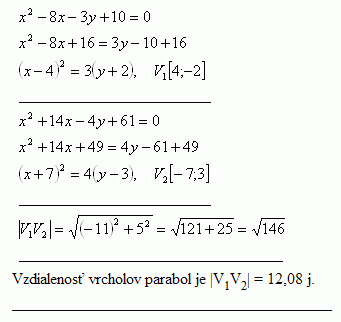
Abstand zwischen den Scheiteln der Parabeln
31.Bestimme die Gleichung einer Parabel (Öffnung parallel zur y-Achse), die durch die Punkte K[1;2], L[3;1], M[7;5] geht.
Lösung:
x2 + Ax + By + C = 0
K: 1 + A + 2B + C = 0
L: 9 + 3A + B + C = 0
M: 49 + 7A + 5B + C = 0
A = -6, B = -4, C = 13,
x2 – 6x – 4y + 13 = 0
x2 – 6x – 4y + 13 = 0
x2 – 6x + 9 = 4y - 13 + 9
(x – 3)2 = 4y – 4
(x – 3)2 = 4·(y – 1)
Die Gleichung der Parabel lautet (x – 3)2 = 4(y – 1).
32.Auf welcher Kurve liegen die Punkte der Ebene, deren Summe der Abstände von der x-Achse und vom Punkt B[8;0] konstant und gleich 24 ist.
Lösung:
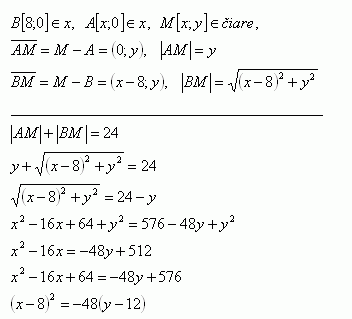
Die Kurve ist die Parabel (x-8)2 = -48(y-12), die sich in negativer y-Richtung öffnet.
33.Die Parabel hat die Gleichung p: y2 = 8x. Berechne die Koordinaten des Quadrats ABCD, wenn A mit dem Scheitel der Parabel zusammenfällt, C auf der x-Achse liegt und die Punkte B, D auf der Parabel.
Lösung:
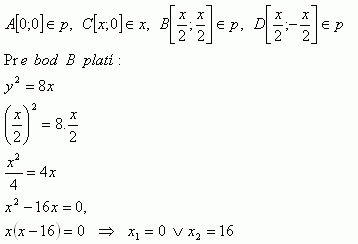
Die Eckpunkte des Quadrats sind: A[0;0], B[8;8], C[16;0], D[8;-8]
34.Bestimme die Seitenlänge eines gleichseitigen Dreiecks ΔABC, das in die Parabel y2 = 5x eingeschrieben ist.
Lösung:
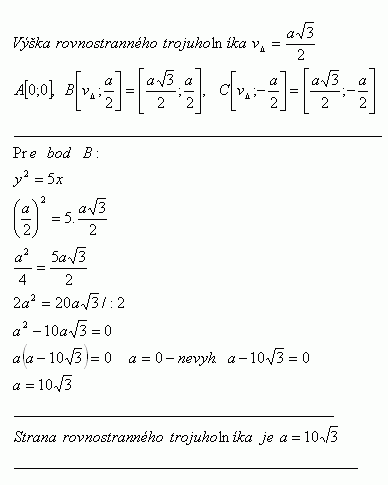
Die Seitenlänge des gleichseitigen Dreiecks ist
35.Berechne die Länge der Sehne, die die Parabel y2 = 2x aus der Ellipse 4x2 + 9y2 – 400 = 0 ausschneidet.
Lösung:
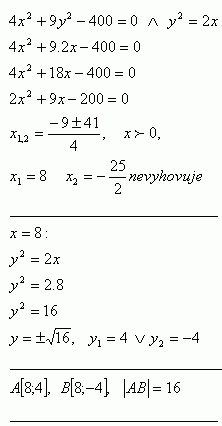
Die Länge der Sehne ist |AB| = 16 j.
36.Bestimme die Lagen der Punkte A, B, C, D, in denen die Ellipse x2 + 2y2 -18 = 0 die Hyperbel x2 – y2 – 9 = 0 schneidet.
Lösung:
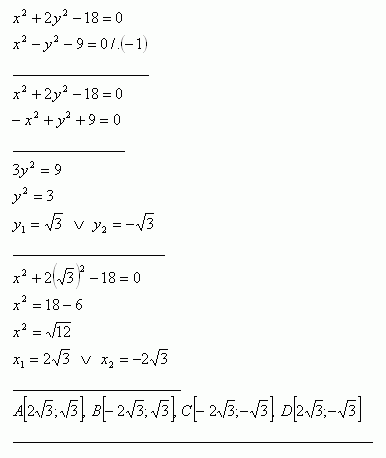
37.Finde auf der Ellipse die Punkte, die vom rechten Brennpunkt den Abstand r = 14 haben (e > 0). Ellipsengleichung:
Lösung:
Ellipse : a2 = 100, b2 = 36, e2 = a2 – b2 = 100 – 36 = 64, e = 8
Kreis : Mittelpunkt = F2[8;0], r = 14
( x – 8 )2 + y2 = 142
x2 – 16x + 64 + y2 – 196 = 0 ⇒ y2 = -x2 + 16x + 132
Ellipse :
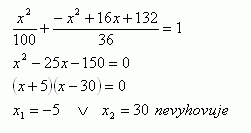
Die gesuchten Punkte:
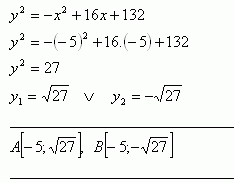
38.Berechne den Umfang des Rechtecks ABCD, dessen Eckpunkte die Schnittpunkte des Kreises k: x2 + y2 = 50 und der Hyperbel h: x2 – y2 = 48 sind.
Lösung:
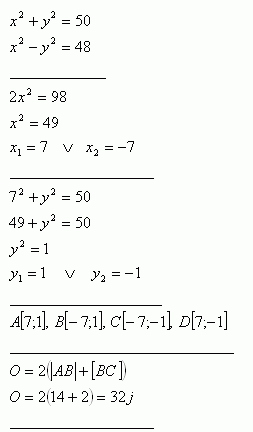
Der Umfang des Rechtecks beträgt P = 32 j