Linie in einer Ebene
1. Erkläre die verschiedenen Arten von Geradengleichungen in einer Ebene.
- Parameterform
- Allgemeine Form
- Steigungsform
- Abstand eines Punktes von einer Geraden
Lösung:
a) Parameterform:

2. Schreibe die Gleichung der Geraden, die durch die Punkte A[2;7] und B[5;1] verläuft, in der Form:
a) Parameterform
b) Allgemeine Form
c) Steigungsform
Lösung:
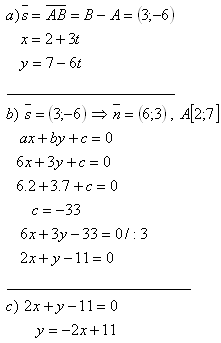
3. Schreibe die Gleichung der Geraden, auf der der Mittelpunkt der Strecke AB liegt, wenn A[1;5] und B[7;3].
Lösung:
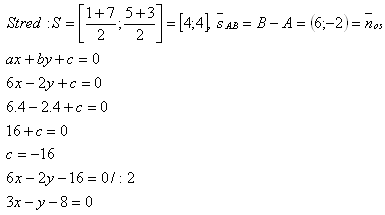
4. Schreibe die Gleichung der Geraden, auf der die Höhe vc im Dreieck A[5;6], B[-2;4] und C[6;-1] liegt.
Lösung:
a) vc: C senkrecht zu AB
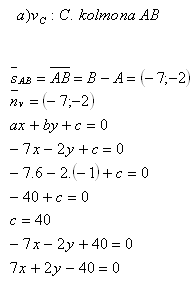
5. Die Gerade (2–m)x + 3my + (2m-6) = 0 ist gegeben.
Bestimme m so, dass:
a) die Gerade durch den Ursprung verläuft
b) die Gerade parallel zur x-Achse ist
c) die Gerade parallel zur y-Achse ist
Lösung:
a)
c = 0
2m – 6 = 0
m = 3
(2–3)x + 3·3y = 0
-x + 9y = 0
x – 9y =0
b)
a = 0
2 – m = 0
m = 2
3·2y + 2·2 – 6 =0
6y -2 = 0/:2
3y – 1 =0
c)
b = 0
2m = 0
m = 0
(2-0)x +(2·0 – 6) = 0
2x – 6 = 0/:2
x – 3 = 0
6. Die Gerade ist gegeben durch p: 4x – 3y +6 = 0
a) Finde heraus, welcher der Punkte A[0;2] und B[-3;5] auf der Geraden liegt
b) wandle sie in die Parameterform um
c) berechne den Abstand des Punktes, der nicht auf der Geraden liegt, von der Geraden
Lösung:
a) A[0;2] liegt auf der Geraden p, weil:
4x -3y +6 = 0
4·0 -3·2 +6 = 0
0 = 0
Punkt B[-3;5] liegt nicht auf der Geraden p, weil:
4x -3y + 6 =0
4·(-3) -3·5 +6 = -21
–21 ≠ 0
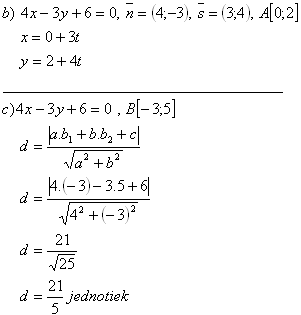
7. Schreibe die Gleichung einer Geraden, die parallel zur Geraden p: 5x +12y -1 = 0 ist und in einem Abstand d = 5 Einheiten von ihr liegt.
Lösung:
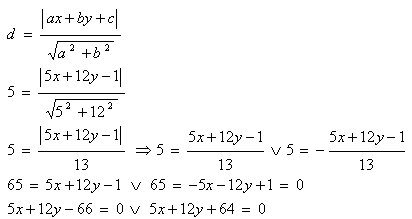
Die gesuchten Geradengleichungen sind q1: 5x + 12y - 66 = 0 und q2: 5x + 12y + 64 = 0
8. Das Dreieck hat die Eckpunkte A[-1;-5], B[9;-1] und C[1;7].
Schreibe:
a) Gleichung der Seite c = AB
b) Gleichung der Medianen tc
c) Gleichung der Höhe auf Seite c, vc
Lösung:
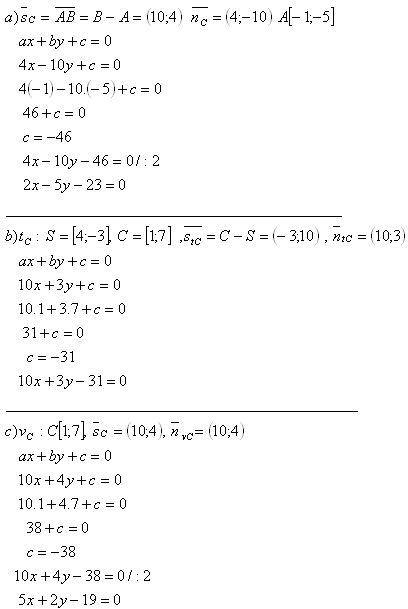
9. Schreibe die Gleichung der Geraden, die mit der x-Achse einen Winkel φ = 135° bildet und durch den Punkt A[3;-1] verläuft.
Bestimme das Segment, das die Gerade auf der y-Achse abschneidet.
Lösung:
A[3;-1]
φ = 135° = 3π/4
Steigung k = tanφ = -1
y = kx + q
-1 = -1·3 + q
q = 2
y = -x + 2
10. Ein Lichtstrahl stammt aus der Quelle A[-1;-5], reflektiert sich an der x-Achse wie an einem Spiegel und verläuft durch den Punkt B[9;-5].
Schreibe die Gleichungen des einfallenden und reflektierten Strahls.
Lösung:

Gleichung des einfallenden Strahls: x – y – 4 = 0
Gleichung des reflektierten Strahls: x + y – 4 = 0
11. Die Scheitelpunkte eines Dreiecks A und B sowie der Schnittpunkt der Höhen Q sind gegeben. Bestimme die Koordinaten des Scheitelpunkts C des Dreiecks, wenn
Lösung:
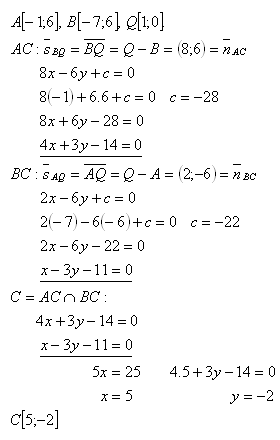
Der Scheitelpunkt C hat die Koordinaten C [5;-2].
12. Finde auf der Geraden p den Punkt C, der von den Punkten A und B gleich weit entfernt ist.
Lösung:
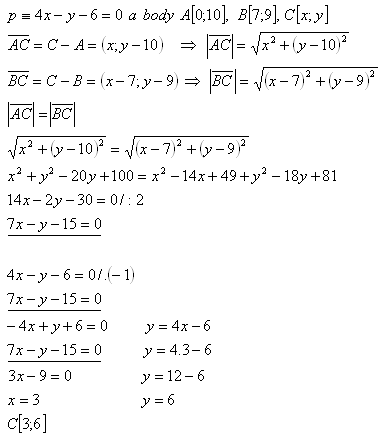
Der Punkt C[3;6] liegt auf der Geraden p.
13. Berechne die Länge der Höhe va im Dreieck ABC, wenn seine Seiten die folgenden Gleichungen haben:
Lösung:
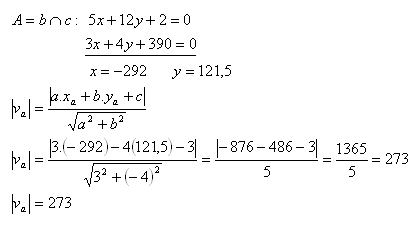
14. Gegenüberliegende Seiten des Quadrats ABCD liegen auf parallelen Geraden.
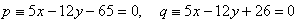
Berechne den Umfang und die Fläche dieses Quadrats.
Lösung:
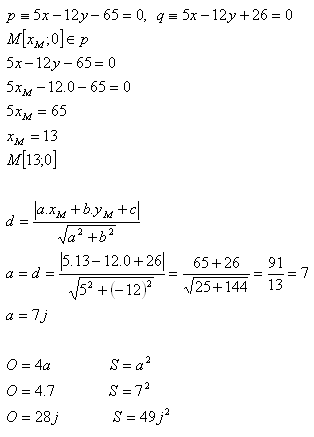
Der Umfang des Quadrats ABCD beträgt 28 Einheiten, seine Fläche beträgt 49 Einheiten2.
15. Bestimme den Umfang und die Fläche des rechtwinkligen Dreiecks, das durch die Gerade 3x + 4y –12 = 0 auf den Koordinatenachsen ausgeschnitten wird.
Lösung:
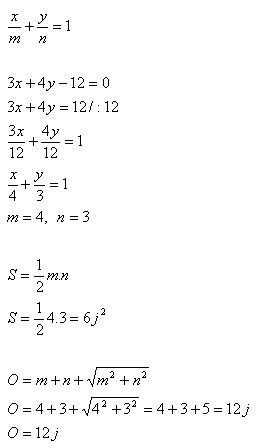
16. Schreibe die Gleichung einer Geraden, die zu 5x + 12y -1 =0 parallel ist und im Abstand d = 5 liegt.
Lösung:
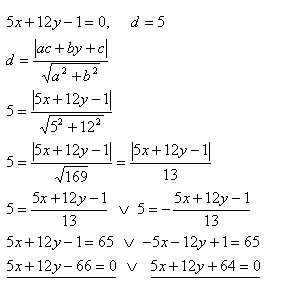
Die gesuchten Gleichungen sind 5x +12y - 66 = 0 und 5x +12y + 64 = 0.
17. Berechne den Abstand des Punktes A[2;-4] von der Geraden 3x + 4y = 0.
Lösung:
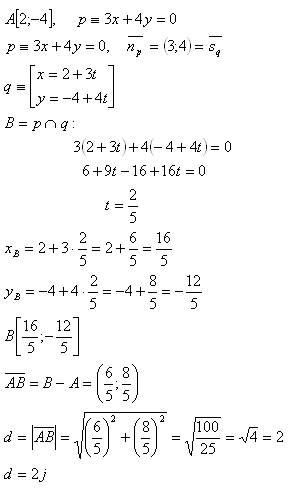
Der Abstand des Punktes A von der Geraden p beträgt d = 2 Einheiten.
18. Die Diagonalen einer Raute u1 = 4, u2 = 6 liegen auf den Koordinatenachsen (u1 auf der x-Achse). Schreibe die Gleichungen der Geraden, auf denen die Seiten der Raute liegen.
Lösung:
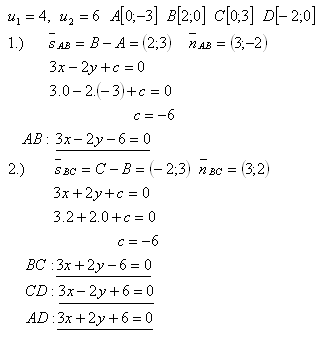
Die Gleichungen der Seiten der Raute sind:
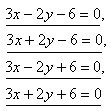
19. Bestimme die Gleichung einer Geraden, die durch den Punkt [2;3] verläuft, so dass das Segment auf der x-Achse halb so lang ist wie das Segment auf der y-Achse.
Lösung:
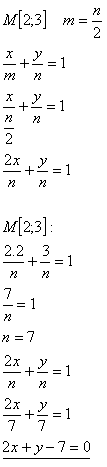
20. Gegeben sind die Punkte A[3;-2], B[1;4], C[-1;-3]. Bestimme den Punkt D so, dass die Gerade CD das Segment AB in seinem Mittelpunkt S schneidet und CD = 3·|CS| gilt.
Lösung:
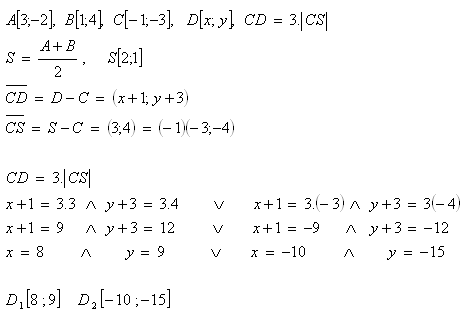
Die Bedingung wird von zwei Punkten erfüllt: D1[8 ; 9] und D2[-10 ; -15].
⁞