Zwei Linien in einer Ebene
1. Charakterisiere die Eigenschaften von zwei Geraden in einer Ebene.
Lösung:
Zwei Geraden p, q in einer Ebene sind:
a) verschiedene parallele Geraden
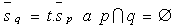
b) identische parallele Geraden
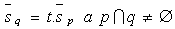
c) sich schneidende Geraden
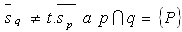
Der Schnittpunkt P zweier sich schneidender Geraden wird durch das Lösen ihres Gleichungssystems bestimmt.
Der Winkel φ zwischen zwei Geraden wird als der Winkel zwischen ihren Richtungs- (oder Normal-)vektoren oder über ihre Steigungen kp, kq bestimmt.
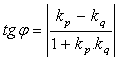
Der Abstand d zwischen zwei parallelen Geraden wird als der Abstand eines Punktes (der zu einer Geraden gehört) zur anderen Geraden bestimmt.
Die Winkelhalbierende zwischen zwei sich schneidenden Geraden ist die Gerade, deren Punkte von beiden Geraden gleich weit entfernt sind. (d
p = d
q)
2. Bestimme die gegenseitige Lage der Geraden p und q, gegeben:
Lösung:
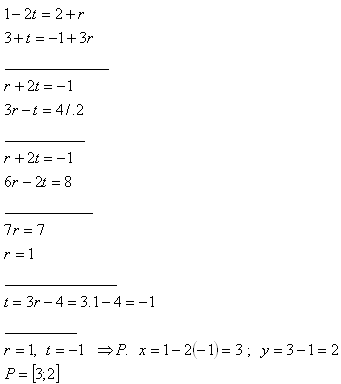
Die Geraden p, q schneiden sich im Punkt P[3;2].
3. Bestimme die gegenseitige Lage der Geraden p und q, gegeben:
Lösung:
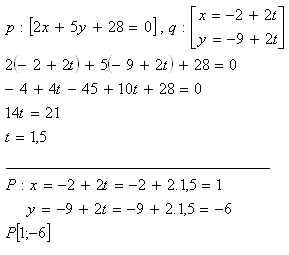
Die Geraden schneiden sich im Punkt P[1;-6].
4. Die Gleichungen der Seiten des Dreiecks ΔABC sind:
a: [x – y + 1 = 0]
b: [2x + 7y – 70 = 0]
c: [7x + 2y -20 = 0]
Berechne die Eckpunkte dieses Dreiecks.
Lösung:
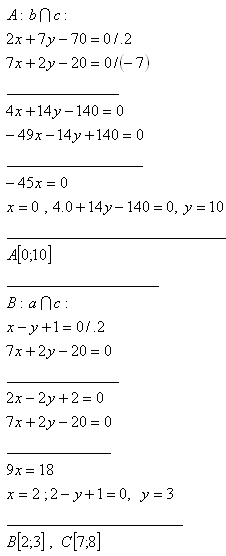
Die Eckpunkte des Dreiecks sind A[0;10], B[2;6] und C[7;8].
5. Gegenüberliegende Seiten eines Quadrats liegen auf parallelen Geraden:
p: [5x - 12y - 65 = 0]
q: [5x - 12y + 26 = 0]
Bestimme die Fläche des Quadrats.
Lösung:
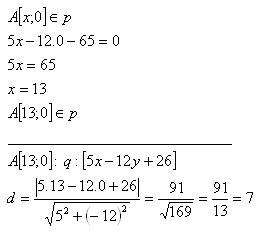
Die Seitenlänge des Quadrats ist d = 7 Einheiten.
S = d2
S = 72
S = 49 E2
Die Fläche des Quadrats beträgt S = 49 E
2.
6. Das Dreieck ΔABC ist durch die Seiten definiert:
a: [x + 3y – 7 = 0]
b: [x – y – 3 = 0]
c: [x – 2y + 3 = 0]
Bestimme:
a) die Eckpunkte des Dreiecks
b) den Mittelpunkt und den Radius des Umkreises des Dreiecks
Lösung:
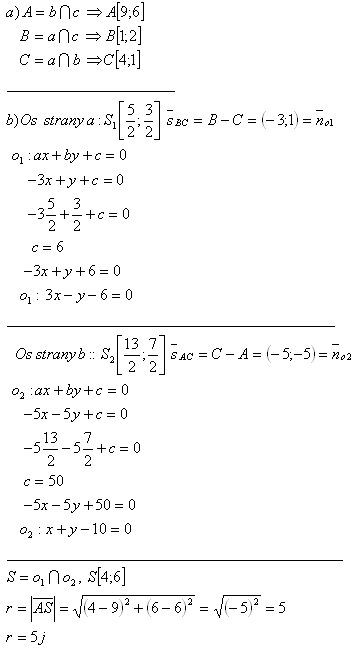
7. Für den Punkt M [1;2], finde den Punkt N [x;y], der symmetrisch zur Geraden p:[x – y - 1 = 0] liegt.
Lösung:
Der gesuchte Punkt N liegt auf der Geraden q, die durch den Punkt M verläuft und senkrecht zu p steht.
Die Punkte M und N sind von der Geraden p gleich weit entfernt.
Es gilt:
p∩q = S, MS = SN
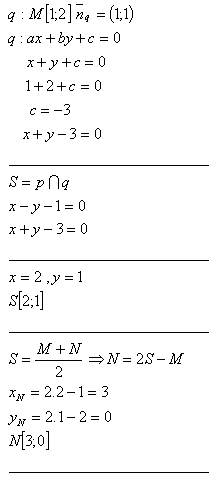
Der gesuchte Punkt ist N[3;0].
8. Schreibe die Gleichung der Winkelhalbierenden der Geraden:
p: [3x – 4y – 2 = 0]
q: [5x – 12y + 26 = 0]
Lösung:
Die Winkelhalbierende der Geraden p und q ist die Gerade, deren Punkte von beiden Geraden gleich weit entfernt sind.
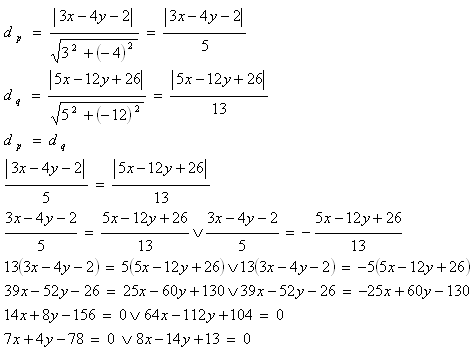
Es gibt zwei Winkelhalbierende (senkrecht zueinander):
o1: [7x + 4y - 78 = 0]
o2: [8x - 14y + 13 = 0]
9. Schreibe die Gleichung der Geraden q, die durch den Punkt M [1;3] verläuft und mit der Geraden p: [2x – y + 5 = 0] einen Winkel φ = 45° bildet.
Lösung:
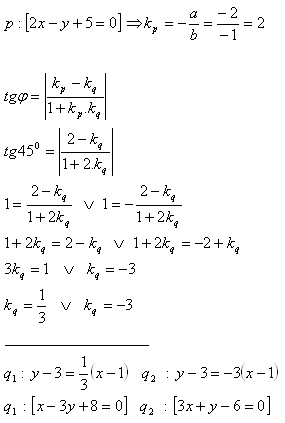
Die gesuchten Geraden sind zwei:
q1: [x – 3y + 8 = 0]
q2: [3x + y – 6 = 0]
10. Drei benachbarte Dörfer haben folgende Positionen auf der Karte:
A[2;-1]
B[5;-2]
C[10;3]
Wo soll das gemeinsame Gemeindezentrum liegen, das von allen drei Dörfern gleich weit entfernt ist?
Lösung:
Die Lage des Gemeindezentrums wird als Schnittpunkt der Mittelsenkrechten der Seiten des Dreiecks ΔABC bestimmt.
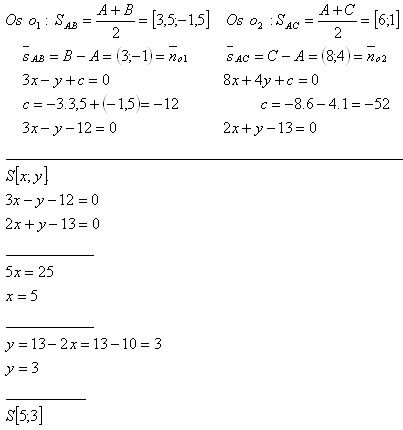
Das Gemeindezentrum liegt im Punkt S[5;3].
11. Finde die Menge aller Punkte in der Ebene, die von den parallelen Geraden gleich weit entfernt sind:
p: [2x – 3y + 10 = 0]
q: [4x – 6y + 5 = 0]
Lösung:
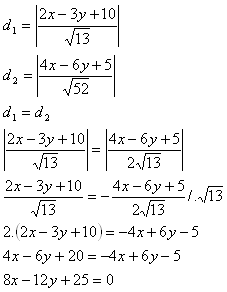
Die gesuchte Menge ist die Gerade o: [8x – 12y + 25 = 0].
12. Auf der Geraden p: [5x – 4y - 28 = 0], bestimme den Punkt, der von den Punkten M [1;5] und N [7;-3] gleich weit entfernt ist.
Lösung:
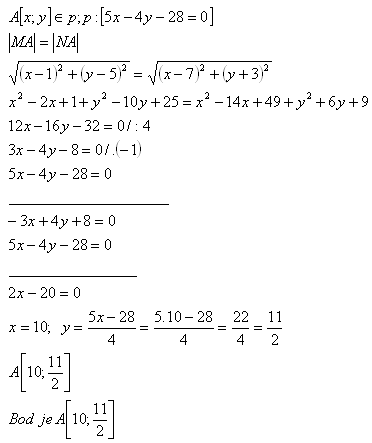
13. Bestimme die Koordinaten des Mittelpunkts des Quadrats ABCD, wenn ein Scheitelpunkt A[-3;-4] gegeben ist und die Diagonale BD auf der Geraden p: [3x +4y – 25 = 0] liegt.
Aufgabenbild
Lösung:
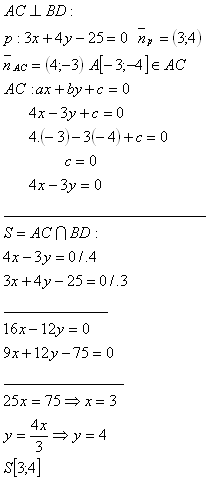
Die Koordinaten des Mittelpunkts des Quadrats ABCD sind S[3;4].
14. Bestimme den geometrischen Ort der Punkte, deren Abstände von den Geraden:
p: [3x + 4y - 23 = 0]
q: [12x – 5y – 13 = 0]
im Verhältnis dp:dq = 2:3 stehen.
Lösung:
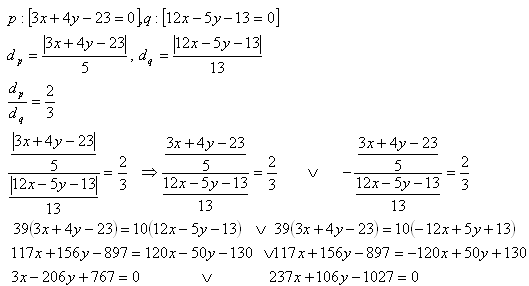
Die geometrischen Orte der Punkte sind die Geraden 3x - 206y + 737 = 0 und 237x + 106y - 1027 = 0.