Molmasse
1. Berechne die Masse in Gramm eines Wasserstoffmoleküls und eines Wasserstoffatoms.
Lösung:
Die molare Masse von molekularem Wasserstoff (H2) beträgt 2,016 g·mol-1. Durch Einsetzen in die Gleichung zur Berechnung der Masse pro Molekül erhält man:
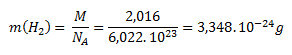
Die molare Masse von atomarem Wasserstoff (H) beträgt 1,008 g·mol-1. Die Masse eines einzelnen Wasserstoffatoms wird analog zum Molekül berechnet:
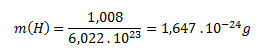
Die Masse eines Wasserstoffmoleküls beträgt 3,348 × 10-24 g und die eines Wasserstoffatoms 1,647 × 10-24 g.
2. Für ein Experiment benötigst du genau 0,1 mol Zink. Welche Masse an Zink muss abgewogen werden?
Lösung:
Wir beginnen mit der Beziehung für die molare Masse. Die molare Masse von Zink aus Tabellen beträgt 65,38 g·mol-1.
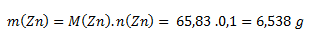
Man muss 6,538 g Zink abwiegen.
3. Kupfer ist ein Gemisch der isotopen Nuklide 63Cu und 65Cu. Die Atommassen dieser Nuklide sind: 63Cu = 62,929 u und 65Cu = 64,928 u (u bezeichnet atomare Masseneinheiten – der Zahlenwert der relativen Atommasse eines Elements und die Masse eines Atoms dieses Elements in u sind gleich). Wenn die relative Atommasse von Kupfer 63,546 beträgt, wie groß ist die prozentuale Häufigkeit der beiden Nuklide im Gemisch?
Lösung:
Die gegebene relative Atommasse von Kupfer ist der gewichtete Mittelwert und hängt von den prozentualen Häufigkeiten der beiden Nuklide im Gemisch ab. Wenn wir die prozentualen Häufigkeiten mit x und y bezeichnen, gelten folgende Gleichungen:
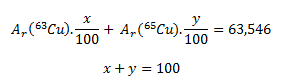
Da die Zahlenwerte der Atommassen in u gleich den relativen Atommassen sind, gilt Ar(63Cu) = 62,929 und Ar(65Cu) = 64,928. Durch Einsetzen dieser Werte erhält man:
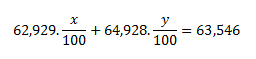
Setze y = 100 − x
0,62929x + 0,64928(100 − x) = 63,546
Die Lösung der Gleichung ergibt die prozentuale Häufigkeit des Nuklids 63Cu:
x = 69,13%
Häufigkeit des Nuklids 65Cu:
y = 100 − x = 100 − 69,13 = 30,87%
Das Gemisch enthält 69,13% 63Cu und 30,87% 65Cu.
4. Berechne die Anzahl der Teilchen des Wirkstoffs in einem homöopathischen Präparat, das durch die Hahnemannsche Centesimalverdünnung C12 hergestellt wird. Dabei wird aus der Urtinktur 1 Teil Lösung entnommen, 99 Teile reines Lösungsmittel hinzugefügt, gemischt und dies insgesamt zwölfmal wiederholt (Verdünnung C12). Die Urtinktur enthält 1 g NaCl in 1 Liter destilliertem Wasser.
Lösung:
Wir beginnen mit den Gleichungen für Stoffmenge und molare Masse.
Die Urtinktur enthält in 1 Liter Salz mit der Masse m0 = 1 g; nach der ersten Verdünnung m1 = 0,01m0; nach der zweiten m2 = 0,012m0; und nach der i-ten Verdünnung mi = 0,01im0. Die Anzahl der NaCl-„Moleküle“ Ni nach der i-ten Verdünnung ist:
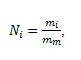 ,
,
wobei mm die Masse eines „Moleküls“ NaCl ist. Der Begriff Molekül ist hier ungenau, da NaCl aufgrund der Ionenbindung in Lösung als Ionen vorliegt.
Nach dem Einsetzen:
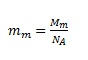
in die erste Gleichung ergibt sich:
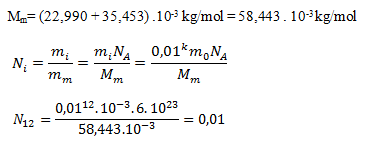
Beim Verdünnungsgrad C12 befinden sich 0,01 Natriumkationen pro Liter Wasser. Bei homöopathischen Behandlungen ist dies üblich – im Wesentlichen handelt es sich um ein Placebo ohne Wirkstoff; jede „Wirkung“ ist psychologisch.
5. Bestimme das chemische Äquivalent von Kupfer in einem Oxid, in dem Kupfer mit Sauerstoff im Massenverhältnis 3,971 : 1,000 verbunden ist.
Lösung:
Das chemische Äquivalent eines Elements hängt von der Oxidationszahl seines Atoms in der Verbindung ab. Aus dem Massenverhältnis von Kupfer und Sauerstoff berechnen wir die Stoffmengen:
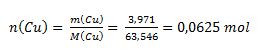
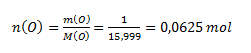
Da n(Cu) : n(O) = 1 : 1, hat das Oxid die Zusammensetzung CuO — Kupfer(II)-oxid. Das Cu-Atom hat die Oxidationszahl II und könnte daher zwei Wasserstoffatome binden. Ein Wasserstoffatom entspricht ½ Atom Kupfer; daher beträgt das chemische Äquivalent des Kupfers im betrachteten Oxid ½ Atom.
6. Wie groß muss die Masse von Calcium sein, damit die Probe die gleiche Anzahl Atome enthält wie 10,00 g Zink?
Lösung:
Vorgehen wie in Beispiel 2.
Ergebnis: 3,44 × 10-22 g
7. Natürliches Lithium ist ein Gemisch der Nuklide 6Li und 7Li mit prozentualen Häufigkeiten von 7,54% und 92,46%. Berechne die relative Atommasse des Nuklids 7Li, gegeben dass die relative Atommasse von 6Li 6,016 beträgt und die durchschnittliche relative Atommasse von natürlichem Li 6,941 ist.
Lösung:
Vorgehen ähnlich wie in Beispiel 3.
Ergebnis: 7,0142
8. Die Masse eines Atoms eines bestimmten Elements beträgt 3,158 × 10-22 g. Berechne die relative Atommasse (d.h. molare Masse) des Elements und bestimme, um welches Element es sich handelt.
Lösung:
Multipliziere die Atommasse mit der Avogadro-Konstanten, um die Masse eines Mols Atome zu erhalten, also die molare Masse des Elements. Das Ergebnis ist 190,21; aus dem Periodensystem lesen wir, dass es sich um Os (Osmium) handelt.
9. Berechne die Stoffmenge des Kristallwassers in 50,4 g Eisen(II)-sulfat-Heptahydrat.
Lösung:
Die molare Masse von Wasser beträgt 18 g/mol; für sieben Wassermoleküle 7 × 18 = 126 g/mol. Die molare Masse von Eisen(II)-sulfat-Heptahydrat beträgt 277,909 g/mol.
In 277,909 g Eisen(II)-sulfat-Heptahydrat ................ 126 g Kristallwasser
In 50,4 g Heptahydrat ................................................................. x g Wasser
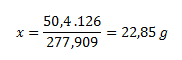
Daraus berechnen wir die Stoffmenge:
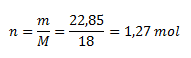
Die Stoffmenge des Wassers im Eisen(II)-sulfat-Heptahydrat beträgt 1,27 mol.
10. Berechne die Stoffmenge:
- a) 5,32 × 1021 Atome Quecksilber (wie in Beispiel 2)
- b) 50 g Quecksilber (wie in Beispiel 2)
- c) wasserfreies Calciumsulfat in 100 g Calciumsulfat-Dihydrat (wie in Beispiel 9)
Lösung:
- a) 8,83 mmol
- b) 0,249 mol
- c) 0,581 mol