Gerade und Kegelschnitt
1. Was weißt du über die gegenseitige Lage einer Geraden und eines Kegelschnitts?
Lösung:
Die gegenseitige Lage einer Geraden und eines Kegelschnitts wird durch das Lösen ihres Gleichungssystems bestimmt, was zum Lösen einer quadratischen Gleichung führt. Wenn
D > 0 ist die Gerade eine Sekante
D = 0 ist die Gerade eine Tangente
D < 0 ist die Gerade keine Sekante
Wenn der Punkt T[xT; yT] der Berührungspunkt ist, der sowohl auf dem Kegelschnitt als auch auf der Geraden liegt, dann gilt:
Gleichungen der Tangenten:

2. Bestimme die gegenseitige Lage der Geraden 2x + y – 8 = 0 und der Parabel x2 + 8y = 0
Lösung:

Die Gerade ist eine Tangente. Sie berührt die Parabel.
3. Bestimme die gegenseitige Lage der Geraden x + y – 10 = 0 und der Ellipse x2 + 3y2 – 3 = 0
Lösung:

Die Gerade ist eine nicht schneidende Gerade.
4. Untersuche die gegenseitige Lage des Kreises k: x2 + y2 -25 = 0 und der Geraden p:
Lösung:
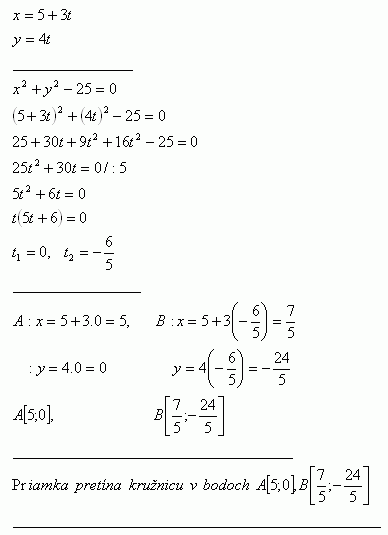
Die Gerade schneidet den Kreis in den Punkten
5. Bestimme c so, dass die Gerade x – y + c = 0 Tangente an die Parabel y2 = 6x ist
Lösung:
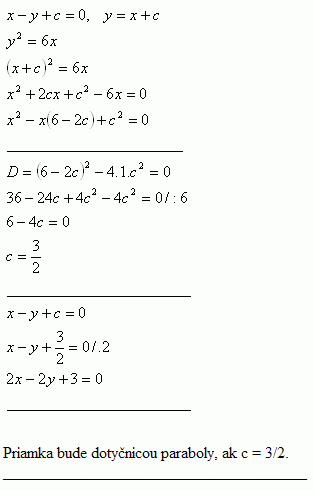
Die Gerade ist eine Tangente der Parabel, wenn
6. Bestimme k so, dass die Gerade y = kx + 3 Tangente an die Hyperbel 16x2 – 25y2 - 400 = 0 ist
Lösung:

Die Tangenten einer Hyperbel haben die Gleichungen
7. Schreibe die Gleichungen der Tangenten an den Kreis x2 + y2 = 25 in seinem Berührungspunkt T [3;y]. Bestimme auch den Winkel φ zwischen den Tangenten.
Lösung:
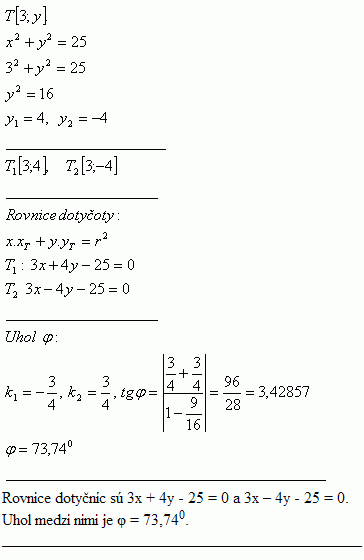
Die Gleichungen der Tangenten sind
Der Winkel zwischen ihnen beträgt
8. Schreibe die Gleichung der Tangente an die Parabel y2 = 18x, die parallel zur Geraden p : 3x – 4y + 69 = 0 ist
Lösung:
Berührungspunkt T [xT ; yT]:
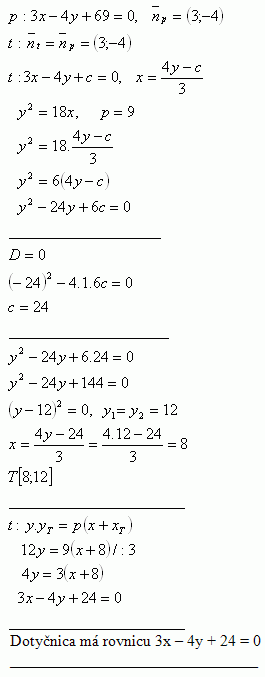
Die Tangenten haben die Gleichungen
9. Bestimme die Länge der Sehnen, die der Kreis auf den Koordinatenachsen abschneidet, wenn die Gleichung des Kreises x2 + y2 – 8x + 7y +12 = 0 lautet
Lösung:
Schnittpunkte mit der x-Achse ( y = 0 ):
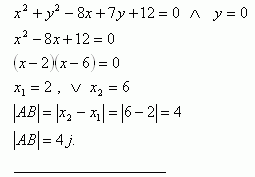
Schnittpunkte mit der y-Achse ( x = 0):
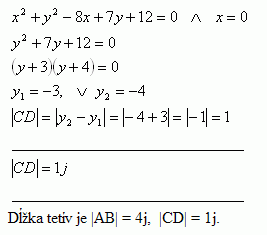
Die Länge der Sehnen beträgt
10. Welche Tangente der Ellipse E: x2 + 4y2 -16 = 0 ist parallel zur Geraden p:
Lösung: