Veränderliches Magnetfeld

1. Gib die grundlegenden Eigenschaften eines nichtstationären Magnetfeldes an.

Lösung:

Ein nichtstationäres Magnetfeld ist ein zeitlich veränderliches Magnetfeld. Die Quelle dieses Feldes ist ein bewegter Permanentmagnet oder Elektromagnet, ein stationärer Leiter mit zeitlich veränderlichem Strom oder ein bewegter stromdurchflossener Leiter.

1.) Magnetischer Fluss Φ:

\Phi = N \cdot B \cdot S \cdot \cos \alpha,\qquad [\Phi] = T \cdot m^2 = Wb = Weber

N = Anzahl der Spulenwindungen
B = magnetische Flussdichte
S = Spulenfläche
α = Winkel zwischen Flussdichte und der Normalen zur Spulenebene

2.) Faradays Gesetz der elektromagnetischen Induktion:

U_e = - \frac{\Delta \Phi}{\Delta t} = - \frac{\Delta (B S)}{\Delta t} = - S \cdot \frac{\Delta B}{\Delta t},\qquad [U_e] = \frac{Wb}{s} = 1V = Volt

3.) Selbstinduktivität L:

L = \frac{\Phi}{I},\qquad [L] = \frac{Wb}{A} = 1H = Henry

U_e = -\frac{\Delta \Phi}{\Delta t} = -\frac{\Delta (L I)}{\Delta t} = - L \frac{\Delta I}{\Delta t}

4.) Induktivität einer Spule:

L = \frac{\mu_0 \cdot \mu_r \cdot N^2 \cdot S}{l},\qquad \mu_0 = 4\pi \cdot 10^{-7}\, N \cdot A^{-2}

5.) Energie des magnetischen Feldes einer Spule:

E_m = \tfrac{1}{2} I \cdot \Phi = \tfrac{1}{2} L I^2,\qquad [E_m] = A \cdot Wb = H \cdot A^2 = 1J = Joule

6.) Magnetische Feldstärke H:

H = \frac{B}{\mu_0 \cdot \mu_r},\qquad [H] = A \cdot m^{-1}

2.Berechne den magnetischen Fluss durch eine rechteckige Schleife mit den Abmessungen a = 4 cm, b = 5 cm in einem Magnetfeld mit der Induktion B = 1,1 T, wenn die Ebene der Schleife einen Winkel β = 30⁰ mit der Richtung der Induktion bildet.

Lösung:

Analyse:

S = a·b = 4 cm·5 cm = 20 cm² = 20·10^–4 m², B = 1,1 T, α = 90⁰ - β = 60⁰

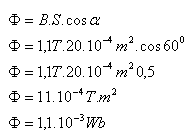
Der magnetische Fluss durch die rechteckige Schleife beträgt φ = 1,1·10^–3 Wb.

3.Wie groß ist die magnetische Induktion B, wenn eine kreisförmige Fläche mit dem Radius r = 5 cm von einem magnetischen Fluss von 4·10^–2 Wb durchsetzt wird? Die Fläche steht senkrecht zu den Feldlinien. (β = 90⁰)

Lösung:

Analyse:

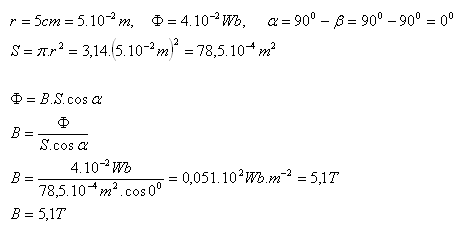
Die magnetische Induktion beträgt B = 5,1 T.

4.Wie groß ist der Radius einer kreisförmigen Spule, deren Achse einen Winkel α = 30⁰ mit B = 5,89 T bildet, wenn ein magnetischer Fluss von 4·10^–2 Wb durch die Spule tritt?

Lösung:

Analyse:

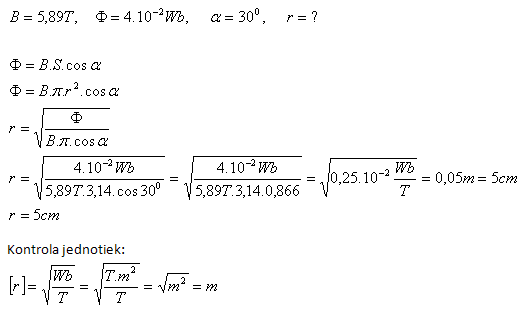
Der Radius der kreisförmigen Spule beträgt r = 5 cm.

5.In welchem Fall wird die induzierte Spannung in einer Leiterschleife größer sein? Wenn der magnetische Fluss in 0,5 s von 1 Wb auf null abnimmt, oder wenn er in 0,1 s von null auf 1 Wb ansteigt? Wie wird die Polarität der induzierten Spannung sein?

Lösung:

a) Der magnetische Fluss nimmt ab

b) Der magnetische Fluss nimmt zu

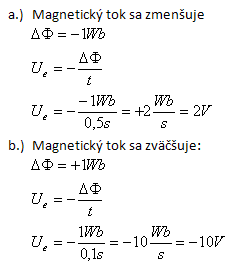
Im Fall b.) wird U_e fünfmal größer sein und die entgegengesetzte Polarität haben.

6.Ein horizontaler Leiter von 2 m Länge wurde zum Zeitpunkt 0 s losgelassen und fiel frei in einer Ebene, die senkrecht zur Nord-Süd-Richtung steht (B = 5·10^–5 T, β = 90⁰). Bestimme die induzierte Spannung an den Enden des Leiters zum Zeitpunkt 5 s.

Lösung:

Analyse:

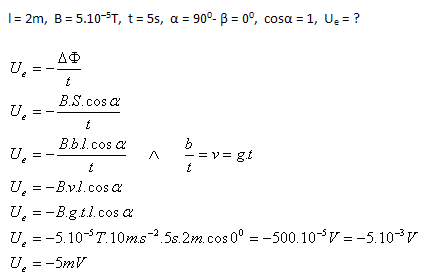
Die induzierte Spannung an den Enden des Leiters beträgt U_e = –5 mV.

7.Bestimme die Selbstinduktivität einer Schleife, wenn eine Stromänderung von ΔI = 0,1 A einen magnetischen Fluss Φ = 4·10^–5 Wb durch den Querschnitt der Schleife hervorruft.

Lösung:

Analyse:

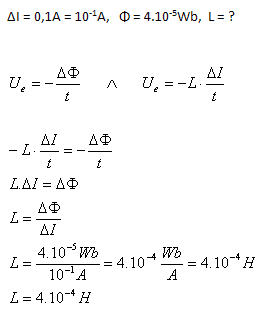
Die Selbstinduktivität der Schleife beträgt L = 4·10^–4 H.

8.Wie viele Windungen hat eine Spule der Länge 30 cm, wenn ein Strom I = 0,5 A ein Magnetfeld der Stärke 833 A·m^–1 im Inneren der Spule erzeugt?

Lösung:

Analyse:

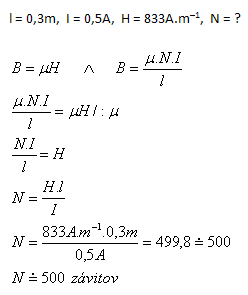
Die Spule hat 500 Windungen.

9.Wie viele Windungen muss eine zylindrische Spule haben, um eine mittlere Spannung von 10 V zu induzieren, wenn sich der magnetische Fluss in ihrem Kern von 0,024 Wb auf 0,056 Wb in 0,32 s ändert?

Lösung:

Analyse:

Die zylindrische Spule muss N = 100 Windungen haben.

10.Berechne die Selbstinduktivität einer luftgekernten Spule mit 1000 Windungen, einer Länge von 20 cm und einem Durchmesser von 2,0 cm. Wie groß ist die Energie des Magnetfeldes, wenn die Spule von einem Strom von 2,5 A durchflossen wird?

Lösung:

Analyse:

Die Selbstinduktivität der Spule beträgt L = 2 mH, und die Energie des Magnetfeldes beträgt E_m = 6,25 mJ.

11. In einem homogenen Magnetfeld mit der magnetischen Induktion B = 30 T bewegt sich ein gerader Leiter mit der Länge l = 1,5 m senkrecht zu den Induktionslinien mit der Geschwindigkeit v = 0,5 m·s^-1. Bestimmen Sie die induzierte Spannung am Ende des Leiters.

Lösung:

Die induzierte Spannung am Ende des Leiters beträgt U_e = –22,5 V.

12.Wie groß war die Änderung der elektrischen Stromstärke in einer Spule mit der Induktivität L = 1,4 H, wenn während des Zeitintervalls Δt = 10^-2 s eine induzierte Spannung U_e = -70 V auftritt?

Lösung:

Die elektrische Stromstärke in der Spule änderte sich um 0,5 A.

13.Eine zylindrische Spule mit 100 Windungen führt einen Strom von 12 A. Der magnetische Fluss in der Spulenöffnung beträgt 5,2 mWb. Berechnen Sie die Energie des Magnetfeldes der Spule.

Lösung:

Die Energie des Magnetfeldes der Spule beträgt E_m = 3,12 J.

14.Das Magnetfeld einer Spule, durch die ein Strom I = 6,2 A fließt, hat eine Energie E_m = 0,32 J. Berechnen Sie die Induktivität der Spule.

Lösung:

Die Induktivität der Spule beträgt L = 16,6·10^-3 H.

15.Der magnetische Fluss eines Hufeisenmagneten beträgt Φ = 20·10^–5 Wb. Bestimmen Sie die magnetische Induktion an den Polen, deren Querschnittsfläche S = 5 cm² beträgt.

Lösung:

Die magnetische Induktion an den Polen des Hufeisenmagneten beträgt B = 0,4 T.

16.Eine zylindrische Drahtspule mit einem Gesamtwiderstand von 160 Ω hat 1000 Windungen und eine Querschnittsfläche von 40 cm². Die Spule wird in ein homogenes Magnetfeld so gelegt, dass ihre Achse parallel zu den Induktionslinien liegt. Die Stärke des Magnetfeldes ändert sich gleichmäßig mit der Zeit so, dass ΔB = 10^-3 T·s^-1 Δt. Bestimmen Sie die in der Spule in 30 Sekunden erzeugte Wärmemenge.

Lösung:

In der Spule werden in 30 Sekunden 3·10^–6 J Wärme erzeugt.

17.Zwei parallele Leiter liegen in einer Horizontalebene im Abstand l = 1 cm. Eine Glühbirne mit dem Widerstand R = 5 Ω ist zwischen den Enden der Leiter angeschlossen. Ein dritter Leiter, der senkrecht zu den gegebenen Leitern steht, kann mit vernachlässigbarer Reibung entlang einer Strecke x gleiten. Das homogene Magnetfeld besitzt eine magnetische Induktion B = 10^-3 T. Bestimmen Sie die Kraft, die angewendet werden muss, um den Leiter mit der konstanten Geschwindigkeit v = 10 cm·s^-1 zu bewegen.

Lösung:

Die auf den Leiter anzuwendende Kraft beträgt F_m = 2·10^–12 N.

18.Berechnen Sie den magnetischen Fluss Φ im Querschnitt der Öffnung einer luftgefüllten zylindrischen Spule. Die Spule hat eine Länge l = 1,6 m, einen Radius r = 4,8 cm, 1400 Windungen und führt einen Strom I = 6,3 A.

Lösung:

Der magnetische Fluss in der Spule beträgt Φ = 5·10^–5 Wb.

19.Ein Strahl von Ionen eines Siliziumisotops mit der Massenzahl 28 und der elektrischen Ladung Q = 1.602·10^-19 C bewegt sich in einem homogenen Magnetfeld B = 0.18 T im Vakuum auf einer Kreisbahn mit dem Radius r = 21 cm. Berechnen Sie die kinetische Energie des Ions.

Lösung:

Die kinetische Energie des Ions beträgt E_k = 4·10^–16 J.

20.Geben Sie die Einheiten der physikalischen Größen Q, B, Φ, L, U, R, W, P als Produkt der grundlegenden SI-Einheiten (kg, m, s, A) an.

Lösung:

Physik

Veränderliches Magnetfeld

Adblock detected