Teilchenladung in einem Magnetfeld
1. Erkläre das Verhalten eines geladenen Teilchens in einem Magnetfeld!
Lösung:
Wenn ein Teilchen mit elektrischer Ladung (Elektron, Proton, Ion, …) senkrecht zu den Induktionslinien in ein Magnetfeld eintritt, wirkt auf das Teilchen eine magnetische Kraft
Fm = B·Q·v.
Unter dem Einfluss dieser Kraft bewegt sich das Teilchen im Feld mit der Geschwindigkeit v, wobei
die Zentrifugalkraft gilt:
Wenn beide Kräfte im Gleichgewicht sind, beschreibt die Bahn des Teilchens einen Kreis mit dem Radius
wobei
r = Radius der Kreisbahn,
v = Geschwindigkeit des Teilchens,
B = magnetische Induktion,
Q = elektrische Ladung des Teilchens.
Es gilt:
Wenn sich das Teilchen in einem elektrischen und einem magnetischen Feld bewegt, gilt die Lorentzkraft:
2. Leite die Formel für den Radius der Kreisbahn eines geladenen Teilchens in einem homogenen Magnetfeld her!
Lösung:
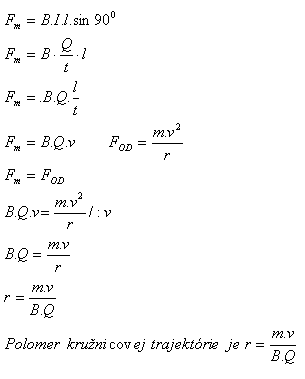
Der Radius der Kreisbahn beträgt
3. Mit welcher Geschwindigkeit bewegte sich ein Proton (mp = 1,673·10–27kg, Qp = 1,602·10-19C) in einem Magnetfeld (B = 1T), wenn seine Bahn ein Kreis mit dem Radius r = 60cm war? Mit welcher Frequenz umkreiste das Proton den Kreis?
Lösung:
Analyse:
mp = 1,673·10–27kg, Qp = 1,602·10-19C, B = 1T, r = 60cm = 0,6m, v = ?, f = ?
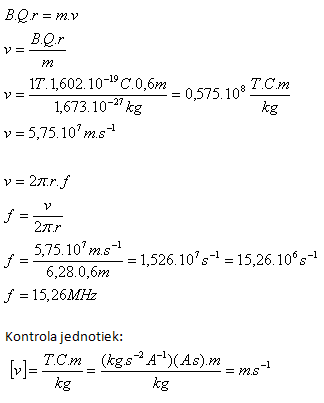
Die Geschwindigkeit des Protons im Magnetfeld beträgt 5,75·107m·s-1, seine Frequenz f = 15,26 MHz.
4. Welche kinetische Energie hat ein Proton (mp = 1,673·10-27kg, Qp = 1,602·10-19C), wenn es sich in einem Kreis mit dem Radius r = 10cm in einem homogenen Magnetfeld mit B = 0,1T senkrecht zu den Induktionslinien bewegt?
Lösung:
Analyse:
mp = 1,673·10-27kg, Qp = 1,602·10-19C, r = 10cm = 0,1m, B = 0,1T, Ek = ?
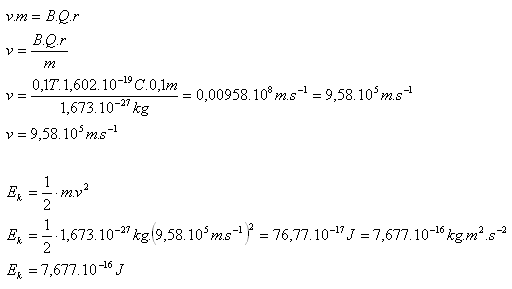
Die kinetische Energie des Protons beträgt Ek = 7,677·10–16J.
5. Ein Elektron (me = 9,1·10–31kg, Qe = 1,602·10–19C) tritt nach der Beschleunigung in einem elektrischen Feld mit U = 100V in ein homogenes Magnetfeld mit B = 10mT senkrecht zu den Induktionslinien ein. Auf welcher Bahn wird sich das Elektron bewegen?
Lösung:
Analyse:
me = 9,1·10–31kg, Qe = 1,602·10–19C, U = 100V, B = 10mT =10–2T
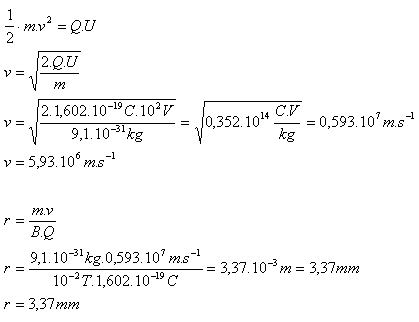
Das Elektron bewegt sich auf einer Kreisbahn mit dem Radius r = 3,37mm.
6. Welche Stärke muss die magnetische Induktion eines homogenen Magnetfelds haben, damit sich ein Elektron mit der Geschwindigkeit v = 3,8·107m·s-1 in einem Kreis mit dem Radius r = 40cm bewegt? Welche kinetische Energie hat das Elektron?
Lösung:
Analyse:
r = 40cm = 0,4m, v = 3,8·107m·s-1, me = 9,1·10–31kg, Q = e = 1,602·10–19C
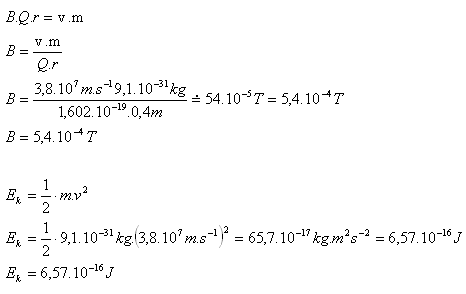
- Die magnetische Induktion muss B = 5,4·10–4T betragen.
- Das Elektron hat eine kinetische Energie von Ek = 6,57·10–16J.
7. Mit welcher Geschwindigkeit müsste sich ein Proton (mp = 1,673·10–27kg, Qp = 1,602·10–19C) im Erdmagnetfeld (B = 5·10–5T – Tabellenwert) senkrecht zu den Induktionslinien bewegen, damit die magnetische Kraft gleich der auf es wirkenden Gravitationskraft ist?
Lösung:
Analyse:
B(Erdmagnetfeld) = 5·10–5T, mp = 1,673·10–27kg, Qp = 1,602·10–19C, g = 10m·s-2
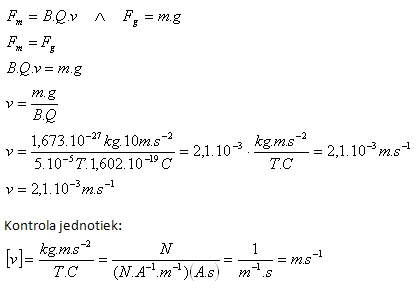
Im Erdmagnetfeld müsste sich das Proton mit der Geschwindigkeit v = 2,1·10-3m·s–1 bewegen.
8. In ein homogenes Magnetfeld mit B = 2·10–5T im Vakuum trat ein Proton (mp = 1,673·10–27kg, Qp = 1,602·10-19C) in einer Richtung senkrecht zu den Induktionslinien ein. Welche Frequenz wird seine Kreisbewegung haben?
Lösung:
Analyse:
2·10–5T, mp = 1,673·10–27kg, Qp = 1,602·10-19C, f = ?
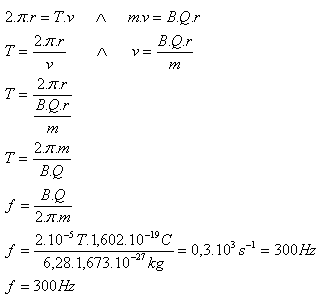
Überprüfe selbst die Einheiten.
Die Frequenz der Kreisbewegung des Elektrons beträgt f = 300Hz.
9. Zwei Elektronen, die sich mit gleicher Geschwindigkeit bewegen, treten in zwei homogene Magnetfelder ein (B1 = 0,1T, B2 = 0,2T) und beginnen sich auf Kreisbahnen zu bewegen. Bestimme das Verhältnis ihrer Umlaufzeiten T1 : T2.
Lösung:
Analyse:
B1 = 0,1T, B2 = 0,2T, T1 : T2 = ?
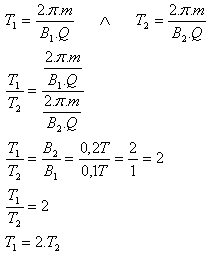
Das Verhältnis der Umlaufzeiten der beiden Elektronen ist T1 : T2 = 2 : 1.
10. Ein Elektron begann sich aus der Ruhe zu bewegen und trat nach dem Durchlaufen einer Potentialdifferenz von 220V senkrecht in ein homogenes Magnetfeld mit der Induktion 5mT ein. Im Magnetfeld bewegte sich das Elektron auf einer Kreisbahn mit dem Radius 1cm. Bestimme die Masse des Elektrons.
Lösung:
Analyse:
U = 220V, B = 5·10–3T, r = 1·10–2m, Q = e =1,602·10–19C, me = ?
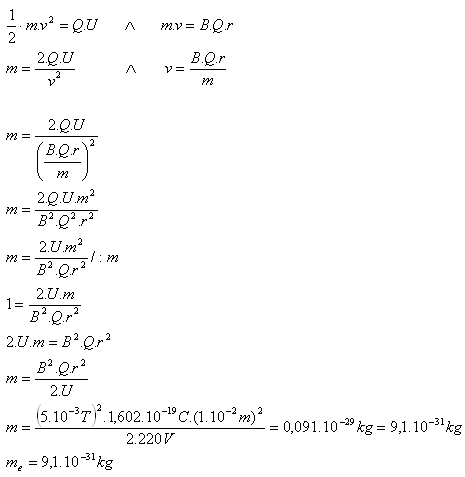
Die Masse des Elektrons beträgt me = 9,1·10–31kg.
11.Ein Proton bewegt sich in einem homogenen Magnetfeld. Die magnetische Induktion des Feldes beträgt B = 15 mT, die Masse des Protons ist mp = 1,67·10–27 kg, seine Ladung ist Qp = 1,602·10–19 C. Bestimmen Sie den Radius seiner kreisförmigen Bahn r, wenn die Geschwindigkeit des Protons v = 2·106 m·s-1 beträgt.
Lösung:
Der Radius der kreisförmigen Bahn des Protons beträgt r = 1,4 m.
12.Ein Teilchen mit der Ladung Q = 1,602·10-19 C ist in ein homogenes Magnetfeld mit der magnetischen Induktion B = 10-2 T eingetreten. In diesem Magnetfeld bewegt es sich auf einem Kreis mit dem Radius r = 0,45·10-2 m. Bestimmen Sie den Betrag des Impulses des Teilchens.
Lösung:
Der Betrag des Impulses des Teilchens beträgt p = 7,2·10–24 kg·m·s–1.
13.Ein Proton bewegt sich mit der Geschwindigkeit v = 1·106 m·s-1 in einem homogenen Magnetfeld mit der magnetischen Induktion B = 1 T.
- Welche Kraft wirkt auf das Proton (mp = 1,673·10–27 kg, QP = 1,602·10–19 C)
- Auf welcher Bahn wird sich das Proton bewegen?
Lösung:
- Die auf das Proton wirkende Kraft beträgt Fm = 1,602·10–13 N.
- Das Proton wird sich auf einem Kreis mit dem Radius r = 1,044 cm bewegen.
14.Ein Elektron tritt nach der Beschleunigung in einem elektrischen Feld mit U = 100 V in ein homogenes Magnetfeld mit der magnetischen Induktion B = 10 mT senkrecht zu den Feldlinien ein. Auf welcher Bahn wird es sich bewegen?
Lösung:
Das Elektron bewegt sich auf einem Kreis mit dem Radius r = 3,4 mm bei der Geschwindigkeit v = 6·106 m·s-1.
15.Welche Spannung muss zwischen Anode und Kathode in einer Glasröhre anliegen, damit die leuchtende kreisförmige Spur, welche die Bahn der Elektronen markiert, den Radius r = 5·10-2 m hat? Die magnetische Induktion in der Röhre beträgt B = 8,2·10-4 T.
Lösung:
Die Spannung zwischen Anode und Kathode beträgt U = 148 V.
16.Ein α-Teilchen bewegt sich auf einer kreisförmigen Bahn mit dem Radius r = 4,5 cm in einem homogenen Magnetfeld mit der magnetischen Induktion B = 1,2 T. Berechnen Sie:
- a.) seine Geschwindigkeit
- b.) seine Umlaufzeit
Lösung:
Die Geschwindigkeit des α-Teilchens beträgt v = 2,6·106 m·s–1, seine Umlaufzeit ist T = 10,86·10–8 s.
17.Ein Protonenstrahl bewegt sich in einer Vakuumröhre so, dass seine Geschwindigkeit v = 0,1c beträgt. Die elektrostatische Kraft ist Fe = 3·10–13 N.
- a.) Wie groß ist das Verhältnis E/B, wenn die resultierende Kraft auf das Proton null ist?
- b.) Wie groß ist die magnetische Induktion B?
Lösung:
Das Verhältnis E/B = v. Die magnetische Induktion beträgt B = 0,062 T.
18.Zwischen Anode und Kathode einer Elektronenkanone in einer Vakuum-Kathodenröhre bewegen sich Elektronen mit der Geschwindigkeit v = 9,19·106 m·s-1. Der Abstand zwischen den Platten beträgt d = 1 cm bei einer Spannung von U = 10 V. Berechnen Sie die Größe der magnetischen Induktion B eines homogenen Magnetfelds, bei dem die Elektronen nicht von der Achse der Röhre abgelenkt werden.
Lösung:
Die magnetische Induktion beträgt B = 0,11 mT.
19.Ein Proton und ein α-Teilchen (mHe = 4·mp, QHe = 2·Qp) treten senkrecht zu den Feldlinien in ein homogenes Magnetfeld ein. Vergleichen Sie die Radien der kreisförmigen Bahnen der Teilchen, wenn beide die gleiche Geschwindigkeit haben.
Lösung:
Der Radius der Bahn des α-Teilchens ist doppelt so groß wie der Radius der Protonenbahn.
20.Ein Elektron ist mit B = 10 mT senkrecht zu den Induktionslinien in ein homogenes Magnetfeld eingetreten, mit der kinetischen Energie Ek = 30 keV. Bestimmen Sie den Radius r seiner kreisförmigen Bahn.
Lösung:
Der Radius der kreisförmigen Bahn des Elektrons beträgt r = 5,83 cm.