Gleichung einer Ebene
1. Auf welche Weise ist eine Ebene im Raum bestimmt?
Lösung:
Eine Ebene im Raum ist durch drei verschiedene Punkte A, B, C bestimmt, die nicht auf derselben Geraden liegen.

2.Gib die allgemeine Gleichung der Ebene an, die den Punkt A [-1;5;0] enthält. Verläuft die Ebene ρ durch den Ursprung? Der Normalenvektor der Ebene ist
Lösung:
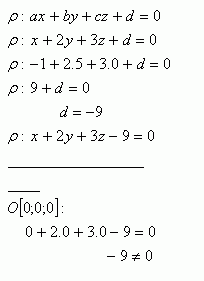
Die Ebene x + 2y + 3z - 9 = 0 verläuft nicht durch den Ursprung.
3. In der Ebene ρ liegen die drei Punkte A[2 ; -4; 5], B[3; -1;4], C[0; -10; 7]. Gib die Parameterdarstellung dieser Ebene an.
Lösung:
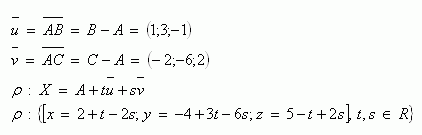
4.Die Ebene ρ ist durch Parametergleichungen gegeben. Wandle sie in die allgemeine Gleichung der Ebene um.
Lösung:
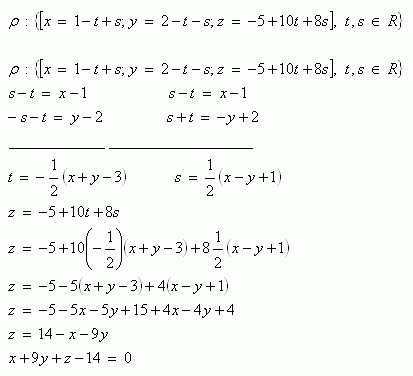
Die Ebenengleichung in allgemeiner Form lautet ρ: x + 9y + z - 14 = 0
5. Bestimme die Gleichung der Ebene σ, die durch den Punkt A [3;4;-5] verläuft und zu den Vektoren
Lösung:

6.Bestimme die Gleichung der Ebene, die durch die Punkte A [2;-4;5], B [3;-1;4], C [0;1;6] verläuft.
Lösung:

Die Gleichung der Ebene lautet 8x + y + 11z – 67 = 0
7. Bestimme die Gleichung der Ebene, die durch zwei parallele Geraden gegeben ist:
Lösung:

Die Gleichung der Ebene ist ρ: 2x + y - 1 = 0
8.Gib die allgemeine Gleichung der Ebene τ an, die zur x-Achse parallel ist und durch die Punkte A[-2;-1;-3], B [2;3;0] verläuft.
Lösung:

Die Gleichung der Ebene ist τ: 3y – 4z - 9 = 0
9. Bestimme die Gleichung der Ebene π, die durch den Punkt M[-4;0;4] verläuft und auf den Koordinatenachsen die Abschnitte p = 4, q = 3 abschneidet.
Lösung:
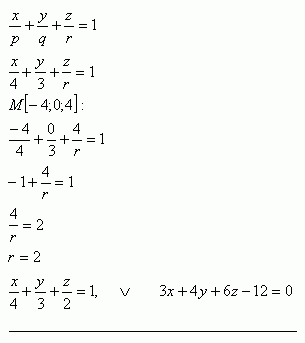
Die Gleichung der Ebene π: 3x + 4y + 6z - 12 = 0
10. Gegeben ist die Ebene ρ : 2x - 2y + z - 6 = 0. Berechne die Winkel zwischen ihrer Normalen und den Koordinatenachsen x, y, z.
Lösung:
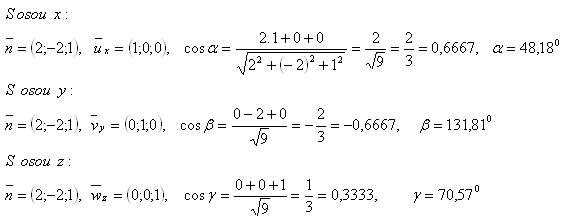
Die Winkel der Normalen mit den Koordinatenachsen sind: α = 48.180, β = 131.810, γ = 70.570
11.Prüfe, ob der Punkt A [22;2;–5] in der Ebene liegt
Lösung:

Der Punkt A liegt in der Ebene ρ.
12.Bestimme die Koordinate „x“ des Punktes M [x;1,2], sodass der Punkt M in der Ebene liegt
Lösung:
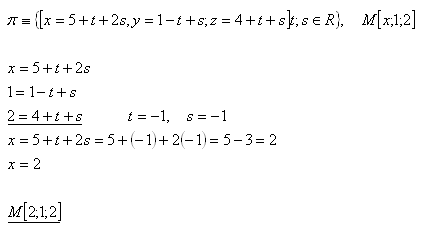
Die gesuchte Koordinate des Punktes M ist x = 2. Der Punkt M ist [2;1;2].
13.Gib die allgemeine Gleichung der Ebene an, die durch den Punkt A verläuft und zur Strecke AB senkrecht ist; gegeben:
Lösung:
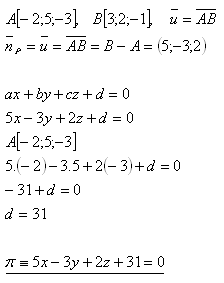
Die Gleichung der Ebene ist π : 5x - 3y + 2z + 31 = 0
14.Gib die allgemeine Gleichung der Ebene τ an, die auf den Koordinatenachsen die Abschnitte p = 2, q = 1, r = 5 abschneidet.
Lösung:
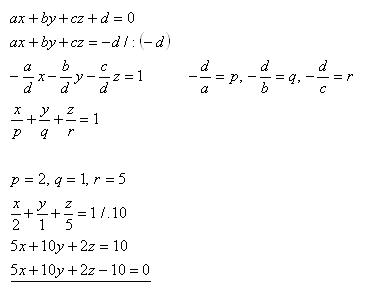
Die Gleichung der Ebene ist τ : 5x + 10y + 2z – 10 = 0
15.Bestimme die Gleichung der Ebene π, die durch den Punkt M verläuft und zur Geraden p senkrecht ist. Löse für die gegebenen Daten:
Lösung:
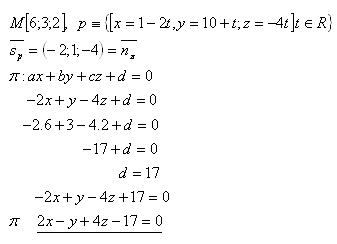
Die Gleichung der Ebene ist π : 2x – y + 4z – 17 = 0
16.Zeige, dass die Punkte A, B, C, D in einer Ebene liegen. Löse für:
Lösung:
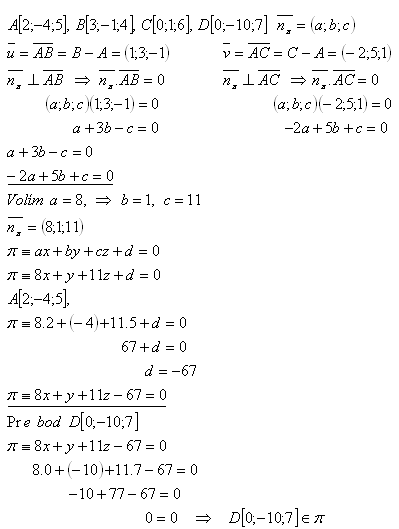
Der Punkt D[0;-10;7] liegt in der Ebene π. Alle Punkte A, B, C, D liegen in der Ebene π.
17.Gegeben sind drei Kugeln π, τ, ρ. Bestimme die allgemeine Gleichung der Ebene χ, die durch die Mittelpunkte dieser Kugeln verläuft. Es gilt:
Lösung:
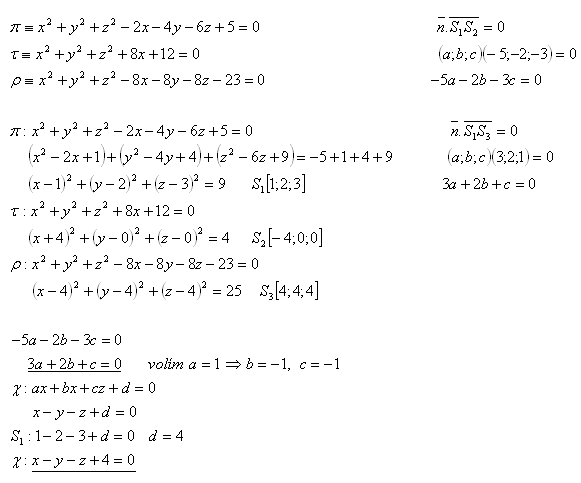
Die Gleichung der Ebene lautet: x – y – z + 4 = 0
18.Gib die allgemeine Gleichung der Ebene π an, die durch die Punkte
Lösung:
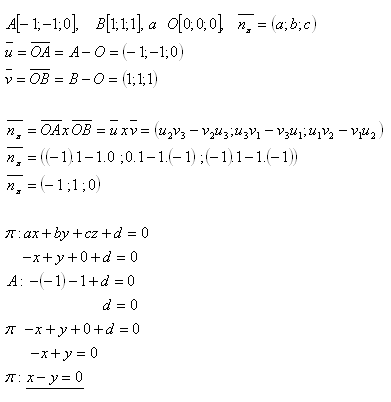
Die Gleichung der Ebene ist π : x – y = 0
19.Wandle die Parameterform der Ebene μ in die allgemeine Form um; gegeben ist
Lösung:
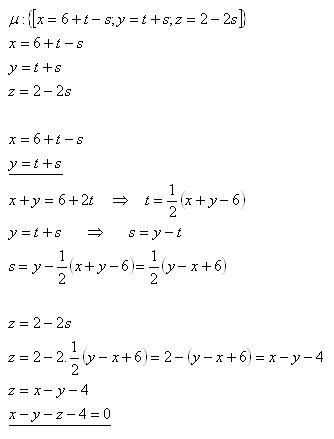
Die Gleichung der Ebene μ in allgemeiner Form ist μ: x – y – z – 4 = 0
20.Für welchen Wert des Parameters „m“ aus ℝ liegt der Punkt M[0;6;m] in der Ebene
Lösung:
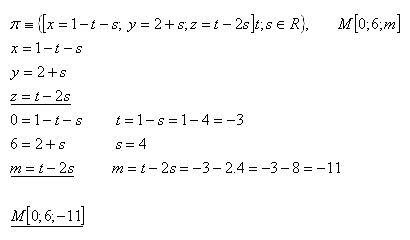
Der Parameter „m“ ist m = –11. Der Punkt M [0;6;–11].