Geraden im Raum

1. Was wissen wir über die Eigenschaften einer Geraden im Raum?

Lösung:

Eine Gerade $p$ ist gegeben durch einen Punkt auf dieser Geraden und ihren Richtungsvektor.

Seien die Punkte $X[x; y; z]$ und $A[a_1; a_2; a_3]$ auf der Geraden $p$ gegeben, und sei
$\vec{u} = \langle u_1; u_2; u_3 \rangle$ ihr Richtungsvektor. Dann gilt:

Parameterdarstellung einer Geraden im Raum:

X = A + t\vec{u}, \quad t \in \mathbb{R}

p:\; \begin{cases} x = a_1 + tu_1 \\ y = a_2 + tu_2,\quad t \in \mathbb{R} \\ z = a_3 + tu_3 \end{cases}

Zwei Geraden $p$ und $q$ im Raum:

Seien $\vec{u}$ , $\vec{v}$ die Richtungsvektoren der Geraden $p$ und $q$ , und sei $P$ ihr Schnittpunkt. Dann können zwei Geraden sein:

a) Parallel und identisch

[\vec{u} = \vec{v} \wedge p \cap q = \{P\}]

b) Parallel und verschieden

[\vec{u} = \vec{v} \wedge p \cap q = \emptyset]

c) Schneidend

[\vec{u} \ne \vec{v} \wedge p \cap q = \{P\}]

d) Windschief (nicht schneidend)

[\vec{u} \ne \vec{v} \wedge p \cap q = \varnothing]

Der Winkel zwischen zwei Geraden wird berechnet als der Winkel zwischen ihren Richtungsvektoren.

2. Schreibe die Parameterdarstellung der Geraden, die durch den Punkt A [2;4;-3] verläuft und parallel zur Geraden BC ist, wobei B [3;2;-1], C [7;1;9]. Bestimme, welcher der Punkte M [-1;2;0], N [6;3;7] auf dieser Geraden liegt.

Lösung:

line-in-space-2

Der Punkt N [6;3;7] liegt auf der Geraden p.

3. Die Gerade p ist parallel zu AB, wenn A [4;-7;2], B [-1;3;6]. Bestimme Y_c und Z_c, sodass der Punkt C [2;Y_c;Z_c] ebenfalls auf dieser Geraden liegt.

Lösung:

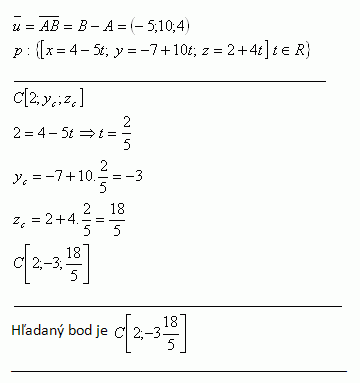
line-in-space-3

4. Gegeben ist das Dreieck ΔABC mit den Eckpunkten A [-2;5;4], B [2;3;-1], C [2;7;-2]. Schreibe die Parameterdarstellungen der Seiten des Dreiecks a = BC, b = AC, c = AB.

Lösung:

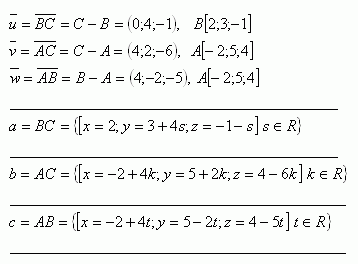
line-in-space-4

5. Gegeben ist Punkt M [3;2;-1] und die Parameterdarstellung der Geraden p

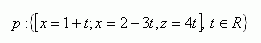
line-in-space-5-problem

Schreibe:

a) die Gleichungen der Geraden q, die durch Punkt M verläuft und parallel zu p ist

b) die Gleichungen der Geraden q, die durch Punkt M verläuft und senkrecht zu p ist

c) die Gleichungen der Geraden q, die parallel zur y-Achse ist

Lösung:

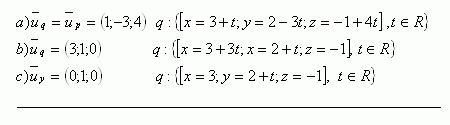
line-in-space-5-solution

6. Bestimme die gegenseitige Lage der Geraden, deren Parameterdarstellungen gegeben sind

Lösung:

line-in-space-6-solution

Die Geraden sind windschief. (t = 1, s = -4 erfüllt die y-Koordinate nicht)

7. Zwei Geraden p und q sind gegeben. Bestimme ihre gegenseitige Lage. Falls sie sich schneiden, bestimme den Schnittpunkt und den Winkel zwischen ihnen.

Lösung:

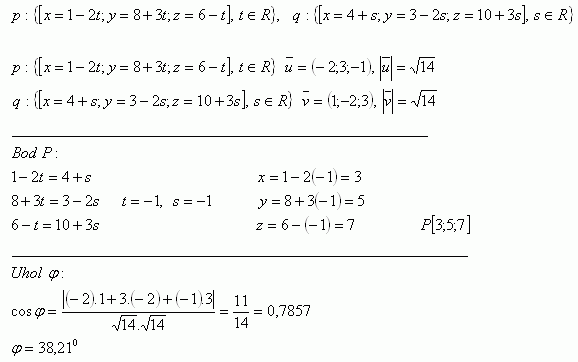
line-in-space-7

Die Geraden schneiden sich im Punkt P [3;5;7] und bilden den Winkel φ = 38,21°.

8. Bestimme die gegenseitige Lage der Geraden p und q, ihren Schnittpunkt und den Winkel, den sie bilden. Berechne außerdem den Abstand des Punktes M [5;-1;4] vom Schnittpunkt der Geraden.

line-in-space-8-problem

Lösung:

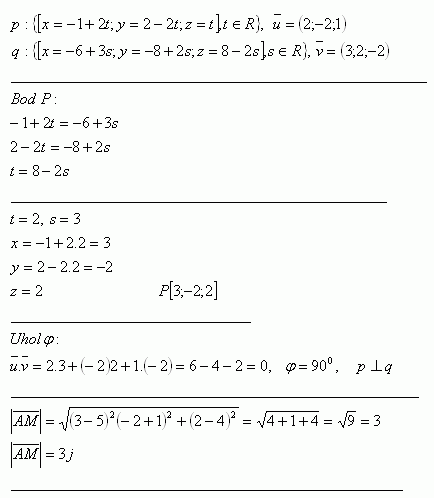
line-in-space-8-solution

9. Entscheide, welcher der Punkte A oder B auf der Geraden p liegt, wenn gilt

Lösung:

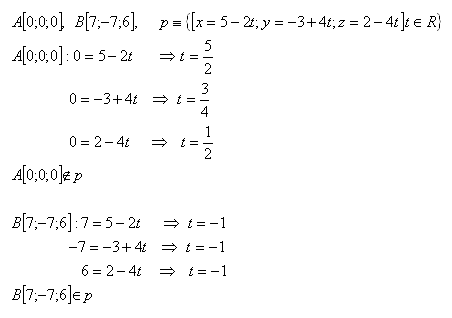
line-in-space-9-solution

Punkt B [7;-7;6] liegt auf der Geraden p.

10. Schreibe die Parameterdarstellung der Geraden, die durch die Punkte A [3;-7;2], B [5;-4;1] verläuft, und bestimme die Koordinaten x, z des Punktes C [x;2;z], sodass er auf der Geraden p liegt.

Lösung:

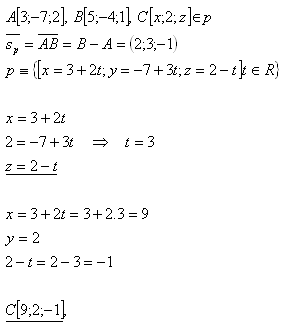
line-in-space-10

Die Koordinaten des gesuchten Punktes sind C [9;2;-1].

11. Bestimme die gegenseitige Lage der Geraden p und q im Raum, wenn gilt:

Lösung:

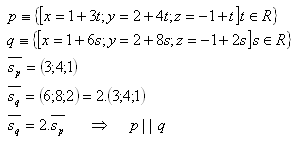
line-in-space-11-solution

Die Geraden p und q sind parallel.

12. Bestimme die gegenseitige Lage der Geraden p und q im Raum, wenn gilt:

Lösung:

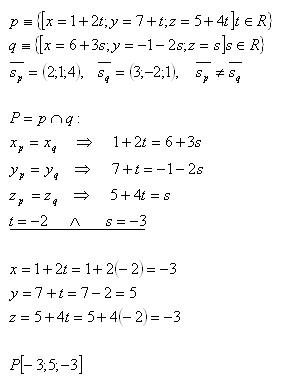
line-in-space-12-solution

Die Geraden p und q sind nicht parallel (sie schneiden sich). Sie schneiden sich im Punkt P [-3;5;-3].

13. Bestimme den Winkel (Neigung) zwischen den Geraden p und q im Raum, wenn gilt:

Lösung:

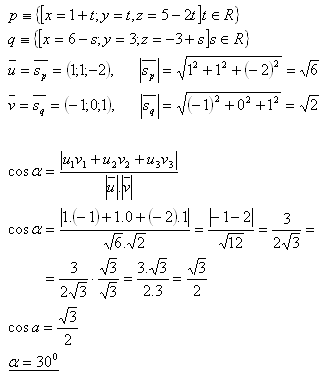
line-in-space-13-solution

Der Winkel zwischen den Geraden p und q beträgt α = 30°.

14. Bestimme den Winkel zwischen den Geraden p und q im Raum, wenn gilt:

Lösung:

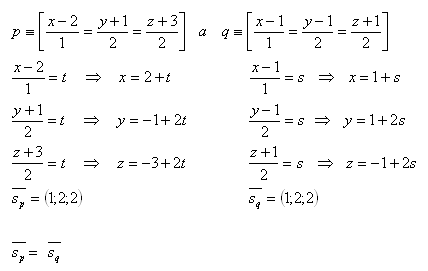
line-in-space-14-solution

Die Geraden p und q sind parallel.

15. Gegeben sind die Punkte A, B, C. Schreibe die Parameterdarstellung der Geraden p, die durch die Mittelpunkte der Strecken AB und BC verläuft. Löse für die Punkte:

Lösung:

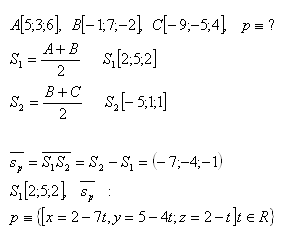
line-in-space-15-solution

16. Berechne den Abstand des Punktes M von der Geraden p, wenn gilt:

Lösung:

line-in-space-16-solution

Der Abstand des Punktes M von der Geraden p beträgt 6 Einheiten.

17. Gegeben sind die Geraden p und q. Finde einen Vektor, der zu beiden Richtungsvektoren der gegebenen Geraden senkrecht ist. Löse für die Geraden:

Lösung:

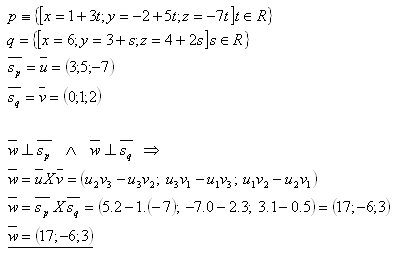
line-in-space-17-solution

18. Gegeben sind die Geraden p und q. Bestimme „m“ so, dass die Geraden nicht parallel (schneidend) sind. Bestimme ihren Schnittpunkt.

Löse für die Geraden:

line-in-space-18-problem

Lösung:

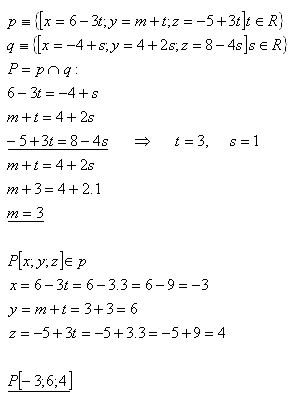
line-in-space-18-solution

Die Geraden p und q sind für m = 3 nicht parallel (sie schneiden sich). Ihr Schnittpunkt ist P [-3;6;4].

19. Berechne den Abstand des Punktes M vom Schnittpunkt der Geraden p und q. Löse für Punkt M [2;3;–23] und die Geraden:

Lösung:

line-in-space-19-solution

Der Abstand zwischen P und M beträgt 25 Einheiten.

20. Gegeben ist Punkt A [-1;4;2]. Bestimme auf der y-Achse den Punkt M so, dass |AM| = 3 gilt. Schreibe außerdem die Parameterdarstellung der Geraden AM.

Lösung:

line-in-space-20-solution

Mathematik

Geraden im Raum

Adblock detected