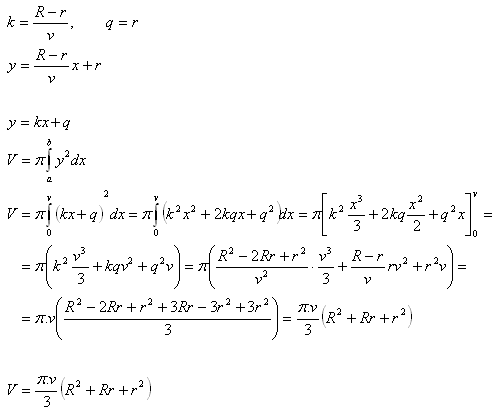Kubikvolumen
1.Erklären Sie den Begriff Kubikvolumen – „Kubatur“!
Lösung:
Kubikvolumen – Kubatur ist die Berechnung des Volumens von Rotationskörpern. Wir berechnen das Volumen eines Körpers, der durch das Rotieren einer Ebenenfigur (Rechteck, Dreieck, Trapez, Kreis usw.) um die x-Achse entsteht. Die Ebenenfigur wird begrenzt durch die x-Achse, die Geraden x1 = a, x2 = b und die Kurve y = f(x).
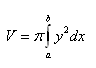
2.Leiten Sie die Formel für das Volumen eines geraden Kreiszylinders mit Grundradius r und Höhe v her.
Lösung:
Der Körper entsteht durch das Rotieren eines Rechtecks um die x-Achse. Das Rechteck wird durch die x-Achse und die Geraden x1=a=0, x2=b=v, y=r begrenzt.
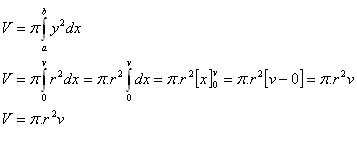
3.Leiten Sie die Formel für das Volumen eines geraden Kreiskegels her, dessen Grundradius r und dessen Höhe v ist.
Lösung:
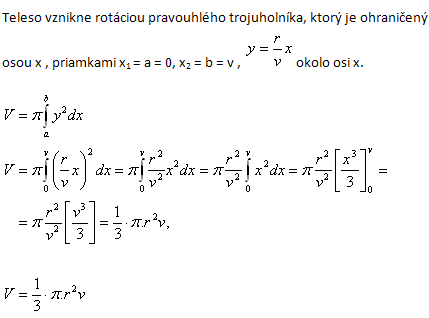
4.Leiten Sie die Formel für das Volumen einer Kugel mit Radius r her!
Lösung:
Der Körper entsteht durch das Rotieren des Kreises x2 + y2 = r2 um die x-Achse.
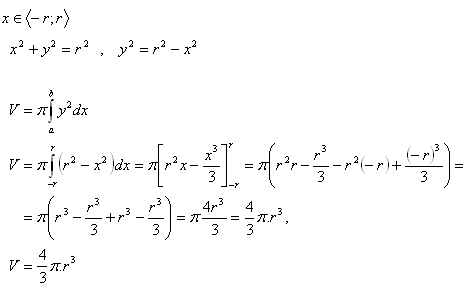
5.Leiten Sie die Formel für das Volumen eines Rotationsellipsoids mit den Halbachsen a, b her.
Lösung:
Der Körper entsteht durch das Rotieren einer Ellipse um die x-Achse. Die Ellipse hat die Gleichung:
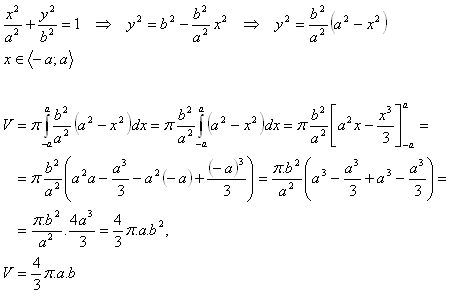
6.Leiten Sie die Formel für das Volumen eines Rotationsparaboloids her, das durch das Rotieren der Parabel y2 = 2px um die x-Achse entsteht. Das Paraboloid hat die Höhe v.
Lösung:
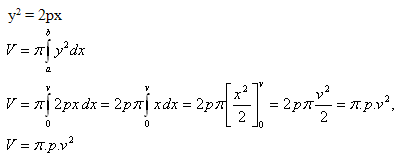
7.Berechnen Sie das Volumen des Körpers, der durch das Rotieren der Funktion y = cos x um die x-Achse entsteht.
Lösung:
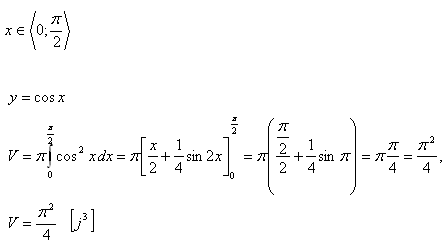
8.Leiten Sie die Formel für das Volumen eines Kegelstumpfes her. Die untere Grundfläche hat Radius R, die obere r. Die Höhe des Kegelstumpfes ist v.
Lösung:
Der Körper entsteht durch das Rotieren eines gleichschenkligen Trapezes um die x-Achse. Das Trapez wird begrenzt durch die x-Achse, die beiden Geraden x1 = a = 0, x2 = b = v und die Linie y = k·x + q, wobei die Konstanten k und q bedeuten