sk|cz|en|

Physik

Elektromagnetische Wellen

1. Charakterisieren Sie das Wesen und die Eigenschaften elektromagnetischer Wellen.

Lösung:

Jede Änderung des Magnetfeldes induziert ein veränderliches elektrisches Feld. Jede Änderung des elektrischen Feldes induziert ein veränderliches Magnetfeld. Das magnetische und das elektrische Feld existieren stets gleichzeitig und bilden ein elektromagnetisches Feld, das sich mit einer Geschwindigkeit von c = 3.108 m.s-1 durch den Raum ausbreitet.

Die Phasengeschwindigkeit der elektromagnetischen Welle ist:

v=1εμv = \frac{1}{\sqrt{\varepsilon \mu}}

Eine fortschreitende elektromagnetische Welle wird durch die Gleichung beschrieben:

u=Umsin⁡(2π(tT−xλ)),λ=cT=cfu = U_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad \lambda = cT = \frac{c}{f} i=Imsin⁡(2π(tT−xλ)),x=Entfernung von der Quellei = I_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad x = \text{distance from source}

Ein Dipol (Strahler, Antenne) ist ein offener schwingender LC-Schwingkreis, der elektromagnetische Wellen aussendet (bzw. empfängt).

Halbwellenstrahler:

l=λ2=c2fl = \frac{\lambda}{2} = \frac{c}{2f}

Die elektromagnetische Welle breitet sich nicht entlang der Leiter aus, sondern entsteht zwischen den Leitern.

Zwei Leiter können verbunden werden:

  • Kurzgeschlossen – am Ende der Leitung ist ein Leiter verbunden; dort ist die Spannung null und es liegt ein Strombauch vor.

  • Leerlauf (offen) – am Ende der Leitung ist kein Leiter verbunden; dort liegt ein Spannungsbauch und ein Stromknoten vor.

Zwischen den Leitern entsteht die Interferenz der einfallenden und der reflektierten Welle → „stehende elektromagnetische Welle“

Amplituden der stehenden elektromagnetischen Welle:


Rλ Spannung Strom
Kurzgeschlossen R→0R \to 0,     λ=4l\lambda    U0=2Umsin⁡2πxλU_0 = 2U_m \sin \frac{2\pi x}{\lambda}     I0=2Imcos⁡2πxλI_0 = 2I_m \cos \frac{2\pi x}{\lambda}
Leerlauf (offen) R→∞,     λ=2l\lambda    U0=2Umcos⁡2πxλU_0 = 2U_m \cos \frac{2\pi x}{\lambda}     I0=2Imsin⁡2πxλI_0 = 2I_m \sin \frac{2\pi x}{\lambda}

 

2. Charakterisieren Sie die einzelnen Arten der elektromagnetischen Strahlung.

  1. Radiostrahlung
  2. Mikrowellen
  3. Infrarotstrahlung
  4. Sichtbares Licht
  5. Ultraviolettstrahlung
  6. Röntgenstrahlung
  7. Gammastrahlung
  8. Kosmische Strahlung

Lösung:


  • Radiostrahlung: f=105 Hz–109 Hz, (λ=102 m–10−1 m)f = 10^{5}\,\text{Hz} – 10^{9}\,\text{Hz}, \; (\lambda = 10^{2}\,\text{m} – 10^{-1}\,\text{m})
    Verwendet zur Übertragung von Ton und Bild – Radio, Fernsehen, Radar.

    Mikrowellen: f=109 Hz–1012 Hz, (λ=10−1 m–10−4 m)f = 10^{9}\,\text{Hz} – 10^{12}\,\text{Hz}, \; (\lambda = 10^{-1}\,\text{m} – 10^{-4}\,\text{m})
    Bewirken thermische Schwingungen von Atomen und Molekülen.

    Infrarotstrahlung: f=1012 Hz–1014 Hz, (λ=10−4 m–10−5 Hz)
    Quellen sind warme Körper – die Sonne, erhitztes Metall usw. Verwendet als Wärmequelle, in Mikrowellenöfen, Fernbedienungen, Fotografie im Dunkeln.

    Sichtbares Licht: f=3.8⋅1014 Hz–7.8⋅1014 Hz, λ=7.9⋅10−7 m–3.86⋅10−7 m

    Ultraviolettstrahlung: f=1015 Hz–1016 Hz, (λ=10−7 m–10−8 m)
    Die Sonne, Quecksilberdampflampen, elektrische Lichtbögen. Verursacht Bräunung der Haut, tötet Bakterien ab, führt in hohen Dosen zu Hautkrebs. Verwendung in sogenannten „Bergsonnen“.

    Röntgenstrahlung: f=1016 Hz–1020 Hz, (λ=10−8 m–10−12 m)
    Entsteht, wenn Kathodenstrahlen auf eine Anode treffen. Wird in der Medizin zur Diagnostik verwendet.

    Gammastrahlung: f=1020 Hz–1024 Hz, (λ=10−12 m–10−16 m)
    Sehr stark durchdringende Strahlung; in kleinen Dosen dient sie zur Behandlung von Krebs, in hohen Dosen entsteht sie bei Kernexplosionen, beim Zerfall von Atomkernen und bei Atombomben.

    Kosmische Strahlung: f=1024 Hz ⇒ (λ=10−16 m)
    Ein Strom von Protonen oder Photonen, der aus dem Weltraum auf die Erde trifft.

    •  

    3. Berechnen Sie die Geschwindigkeit elektromagnetischer Wellen im Vakuum und in Wasser, gegeben ist für Wasser εr=81, μr=1.

    Lösung:

    Analyse:

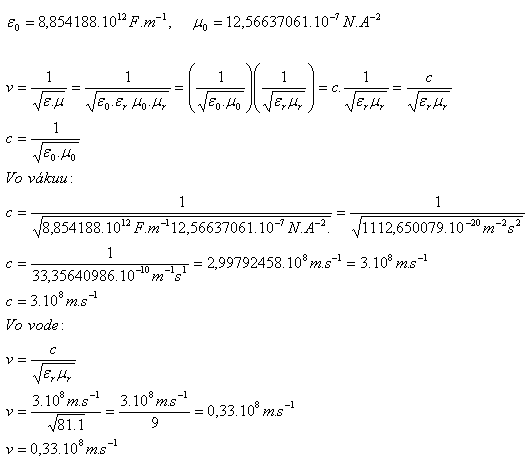
    fyzika-elektromagneticke-vlnenie-3.gif 

    Die Geschwindigkeit elektromagnetischer Wellen im Vakuum beträgt c = 3.108 m.s-1, und in Wasser v = 0,33.108 m.s-1.

    4. Das UKW-Funkband hat einen Frequenzbereich von 66 MHz bis 73 MHz. Bestimmen Sie die kleinste und die größte Wellenlänge der elektromagnetischen Wellen in diesem Band.

    Lösung:

    Analyse:

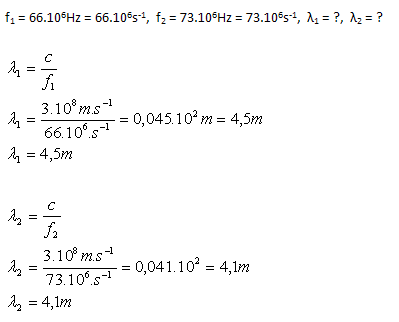
    fyzika-elektromagneticke-vlnenie-4.gif 

    Der Wellenlängenbereich im UKW-Funkband liegt zwischen 4.1 m und 4.5 m.

    5. Bestimmen Sie die Länge eines Halbwellen-Dipols, der die Kapazität 10 pF und die Induktivität 0.9 μH hat. (c = 3.108 m.s-1)

    Lösung:

    Analyse:

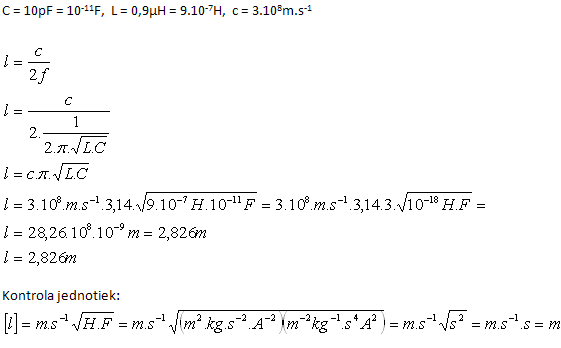
    fyzika-elektromagneticke-vlnenie-5.gif 

    Der Halbwellen-Dipol hat die Länge l = 2.826 m.

    6. Der Schwingkreis eines Empfängers ist auf den Empfang einer Übertragung mit elektromagnetischen Wellen der Wellenlänge 5 m abgestimmt. Bestimmen Sie die Induktivität der Spule im Schwingkreis, wenn seine Kapazität 20 pF beträgt.

    Lösung:

    Analyse:

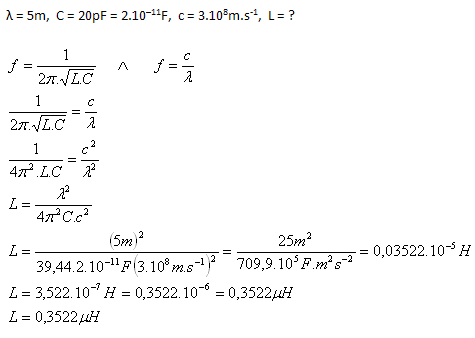
    fyzika-elektromagneticke-vlnenie-6.gif 

    Die Induktivität der Spule im Schwingkreis beträgt 0.3522 μH.

    7. Der Schwingkreis eines Senders besteht aus einer Spule mit L = 50 μH und einem Kondensator, dessen Kapazität von 60 pF bis 240 pF veränderlich ist. Bestimmen Sie den Wellenlängenbereich der elektromagnetischen Wellen, in dem der Sender arbeitet.

    Lösung:

    Analyse:

    fyzika-elektromagneticke-vlnenie-7.gif 

    Der Sender arbeitet in einem Wellenlängenbereich von 103.2 m bis 206.3 m.

    8. Eine sehr lange Zweidraht-Leitung ist an eine Wechselspannungsquelle mit der Amplitude 1 V und der Frequenz 75 MHz angeschlossen. Bestimmen Sie die Momentanspannung zwischen den Drähten in einem Abstand von 5.5 m von der Quelle zu dem Zeitpunkt, zu dem die Quellspannung null ist.

    Lösung:

    Analyse:

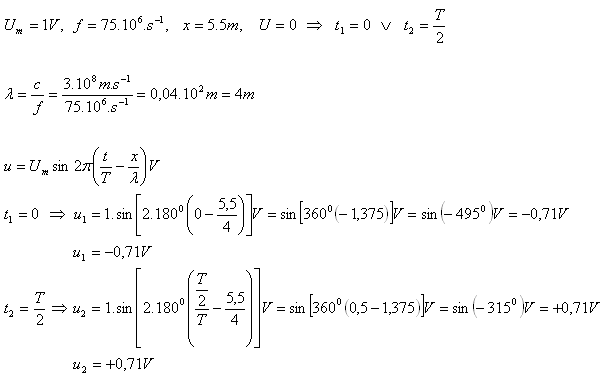
    fyzika-elektromagneticke-vlnenie-8.gif 

    Die Momentanspannungen sind u1 = –0.71 V und u2 = 0.71 V.

    9. Zwischen zwei langen Leitern bildet sich eine stehende elektromagnetische Welle. Die Leiter sind offen geschaltet. In welchem Abstand von den Enden der Leiter befindet sich

    • a) ein Strombauch der stehenden elektromagnetischen Welle
    • b) ein Stromknoten der stehenden elektromagnetischen Welle

    Lösung:

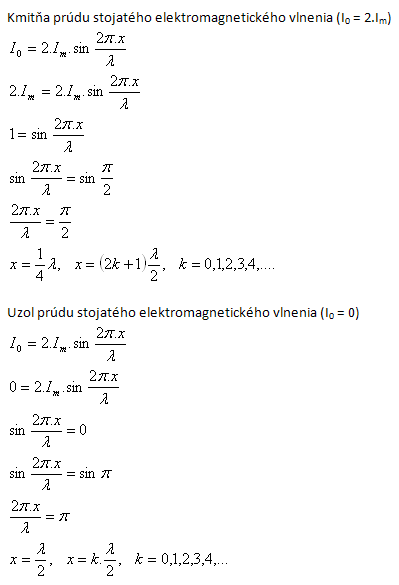
    fyzika-elektromagneticke-vlnenie-9.gif

    10. Ein elektromagnetischer Dipol für den Empfang in Luft hat die Länge l = 1.8 m. Bestimmen Sie seine Länge für den Empfang elektromagnetischer Wellen derselben Frequenz in Wasser. (εr = 81, μr = 1)

    Lösung:

    Analyse:

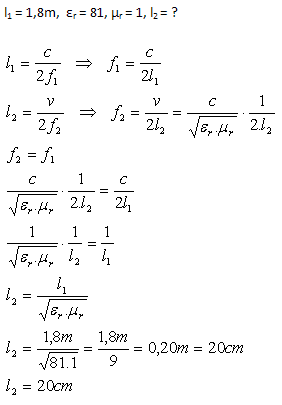
     fyzika-elektromagneticke-vlnenie-10.gif

    Die Länge des elektromagnetischen Dipols in Wasser beträgt 20 cm.

    11. Ein Schwingkreis ist durch L1 = 3.10-3 H und C1 = 2.10-6 F charakterisiert, der andere durch L2 = 4.10-3 H und C2 = 1.10-6 F.

    • Befinden sich die Schwingkreise in Resonanz?
    • Falls nicht, nehmen Sie eine Korrektur vor.

    Lösung:

    Analyse:

    L1 = 3.10-3 H und C1 = 2.10-6 F, L2 = 4.10-3 H und C2 = 1.10-6 F.

    Bedingung für Resonanz:
    L1·C1 = L2·C2
    3.10-3 H · 2.10-6 F = 4.10-3 H · 1.10-6 F
    6.10-6 H·F = 4.10-9 H·F — nicht erfüllt

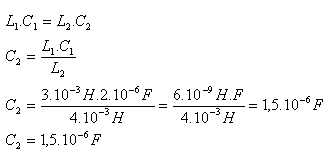
     fyzika-elektromagneticke-vlnenie-11.gif

    Die Schwingkreise sind nicht in Resonanz. Es gibt mehrere Möglichkeiten, dies zu korrigieren. Zum Beispiel kann man den Kondensator C2 = 1.10-6 F durch einen anderen Kondensator C2 = 1.5.10-6 F ersetzen.

    12. Elektromagnetische Radiowellen mit der Wellenlänge λ1 = 375 m treffen auf die Grenzfläche zweier Medien. Der Einfallswinkel ist α = 350, der Brechungswinkel β = 330. Wie groß ist die Wellenlänge dieser Wellen λ2 im zweiten Medium?

    Lösung:

    Analyse:

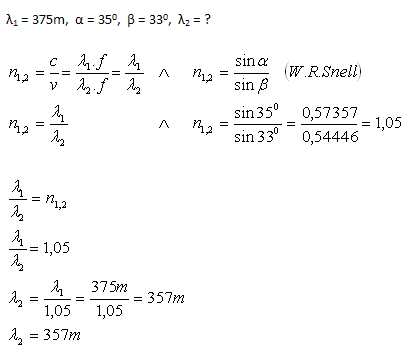
    fyzika-elektromagneticke-vlnenie-12.gif 

    Die Wellenlänge im zweiten Medium beträgt λ2 = 357 m.