Wechselstrom

1.Erklären Sie die Begriffe der Effektivwerte von Wechselstrom und -spannung sowie die Leistung des Wechselstroms.

Lösung:

Messgeräte messen nicht die momentanen oder maximalen Werte von Strom und Spannung, sondern die „Effektivwerte“ von Strom und Spannung.

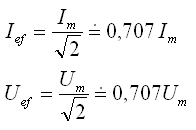
Leistung des Wechselstroms in einem Stromkreis mit einem Widerstand:

P = R I_m^2 \sin^2 (\omega t), \qquad [P] = \text{W}

Leistung des Wechselstroms in einem Stromkreis mit Impedanz:

a) Wirkleistung des Wechselstroms

P = I U \cos \varphi \qquad [P] = 1\,\text{W}

b) Blindleistung des Wechselstroms

P_Z = I U \qquad [P_Z] = 1\,\text{V⋅A}

c) Scheinleistung des Wechselstroms

P_Q = I U \sin \varphi \qquad [P_Q] = 1\,\text{V⋅Ar}

$I, U$ sind Effektivwerte (RMS-Werte).

Beziehung zwischen den einzelnen Leistungsanteilen des Wechselstroms:

P_Z^2 = P^2 + P_Q^2

Leistungsfaktor:

\cos \varphi = \frac{P}{I U}, \qquad 0 < \varphi < \frac{\pi}{2}

Wirkungsgrad eines Elektromotors:

\eta = \frac{P_2}{P_1} \cdot 100\% = \frac{U I \cos \varphi}{P_{Z2}} \cdot 100\

$P_{1} =$ Wirkleistung des elektrischen Stroms
$P_{2} =$ Leistung des Elektromotors

2.Ein Widerstand mit R = 20Ώ ist an eine Wechselspannungsquelle U_ef = 24V und f = 50Hz angeschlossen. Stellen Sie die Gleichung für den momentanen Wert des Stroms im Stromkreis auf. Bestimmen Sie den Effektivwert des Stroms im Stromkreis.

Lösung:

Analyse:

R = 20Ώ, U_ef = 24V, f = 50s^-1, I_ef = ?

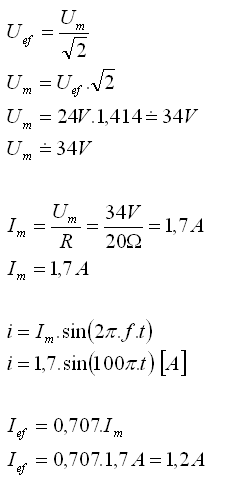
Die Gleichung für den momentanen Wert des Stroms im Stromkreis lautet i = 1.7.sin(100π.t) [A].
Der Effektivwert des Stroms im Stromkreis ist I_ef = 1.2A.

3.Bestimmen Sie die Zeitpunkte innerhalb einer Periode der Wechselspannung, zu denen die Momentanspannung der Effektivspannung entspricht.

Lösung:

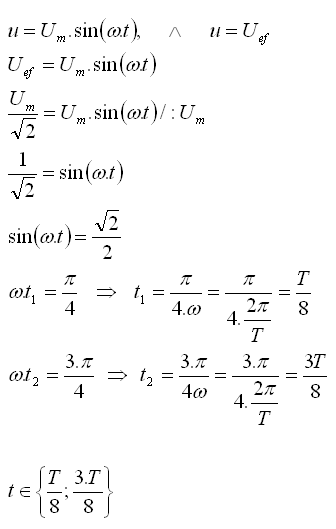
Die Momentanspannung ist gleich der Effektivspannung bei t₁ = T/8 und t₂ = 3T/8.

4.Die Wechselspannung hat einen Effektivwert von U_ef = 156V. Bestimmen Sie die Amplitude der Spannung. Nach welcher Zeit seit dem Anfangszeitpunkt erreicht der momentane Wert der Wechselspannung den Effektivwert, wenn f = 50Hz ist?

Lösung:

Analyse:

U_ef = 156V, f = 50Hz = 50s^–1, U_m = ?, t = ?

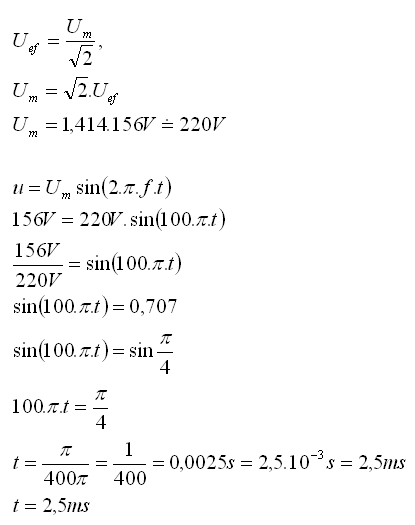
Der momentane Wert der Wechselspannung erreicht den Effektivwert nach t = 2.5ms.

5.Für die momentanen Werte von Strom und Spannung in einem Wechselstromkreis gelten die folgenden Gleichungen: i = 1.sin(100π.t – π/4) [A] und u = 150.sin(100π.t) [V]. Bestimmen Sie die Wirkleistung, Scheinleistung und Blindleistung dieses Stroms. Zeigen Sie, dass gilt:

Lösung:

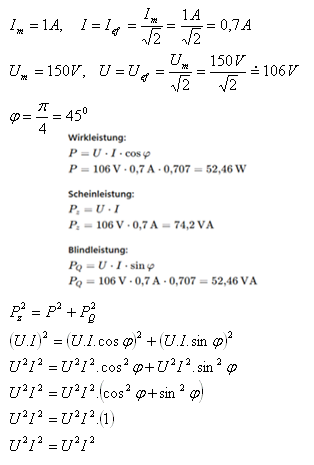
ac-power-5-en

6.Berechnen Sie die Wirkleistung des Wechselstroms, der an eine Wechselspannungsquelle (U = 220V, f = 50Hz, cos φ = 0.8) angeschlossen ist, wenn der Stromkreis eine Last mit folgenden Eigenschaften enthält:

a.) Spule mit Induktivität L = 0.1H
b.) Kondensator mit Kapazität C = 10^-3F

Bestimmen Sie, wie sich die Wirkleistung des Wechselstroms mit der Frequenz ändert.

Lösung:

Analyse:

U = 220V, f = 50Hz, cos φ = 0.8

a.) Spule mit Induktivität L = 0.1H

b.) Kondensator mit Kapazität C = 10^-3F

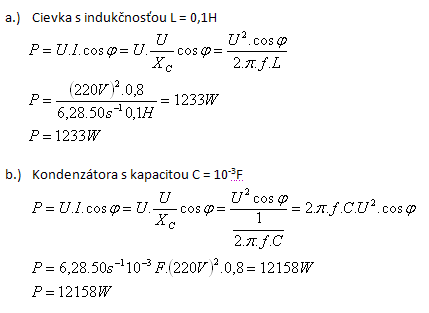
Wenn eine Spule im Stromkreis angeschlossen ist und die Frequenz steigt, nimmt die Wirkleistung ab (f steht im Nenner).
Wenn ein Kondensator im Stromkreis angeschlossen ist und die Frequenz steigt, nimmt die Wirkleistung zu (f steht im Zähler).

7. Berechnen Sie den Strom, der durch einen einphasigen Wechselstrommotor fließt, wenn er eine Leistung von 5kW hat und an eine 220V-Versorgung angeschlossen ist. Der Leistungsfaktor des Motors beträgt 0.85 und sein Wirkungsgrad 80%.

Lösung:

Analyse:

P = 5000W, U = 220V, cosφ = 0.85, η = 0.8

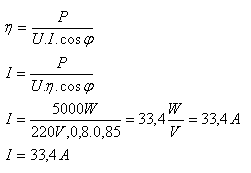
Der Strom, der durch den einphasigen Motor fließt, ist I = 33.4A.

8. Bei einer Spannung von 48V beträgt der Strom im Stromkreis 6A. Die Wirkleistung im Stromkreis ist 200W. Berechnen Sie den Leistungsfaktor. Beurteilen Sie, wie sich die Wirkleistung des Geräts ändern würde, wenn der Leistungsfaktor auf 0.98 verbessert würde.

Lösung:

Analyse:

U = 48V, I = 6A, P₁ = 200W, φ₁ = ?, cos φ₂ = 0.98

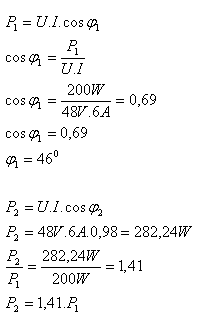
Die Wirkleistung erhöht sich um das 1.41-fache (um 41%).

9. Eine Wechselspannung von 3000V mit f = 50Hz ist in Reihe mit einem Widerstand R = 40Ώ und einer Spule mit Induktivität L = 95·10^-3H geschaltet. Bestimmen Sie den Strom im Stromkreis, die Phasenverschiebung zwischen Strom und Spannung und die Wirkleistung des Stroms.

Lösung:

Analyse:

U = 3000V, f = 50Hz, R = 40Ώ, L = 95·10^-3H, I = ?, φ = ?, P = ?

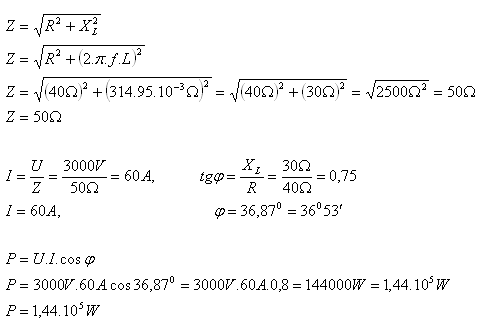
Der Strom im Stromkreis ist I = 60A, die Phasenverschiebung φ = 36°53‘, und die Wirkleistung beträgt 1.44·10⁵W.

10. Ein einphasiger Motor hat bei einer Spannung von 220V und einem Strom von 10A 5 Minuten lang gearbeitet. Der Stromzähler registrierte in dieser Zeit 0.125 kWh. Bestimmen Sie den Leistungsfaktor des Motors.

Lösung:

Analyse:

t = 5 min = 300s, I = 10A, U = 220V, W = 0.125 kWh (1kWh = 3.6·10⁶J) W = 0.125·3.6·10⁶J = 0.45·10⁶J

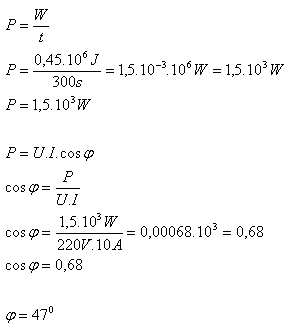
Der Leistungsfaktor des Motors ist cos φ = 0.68.

Physik

Wechselstrom

Adblock detected